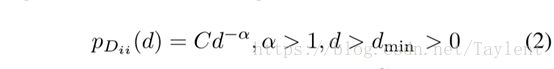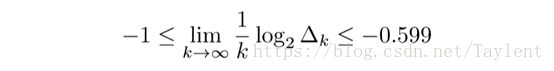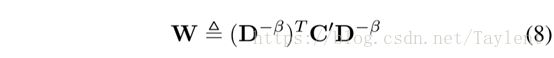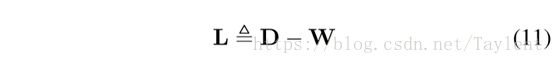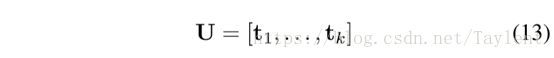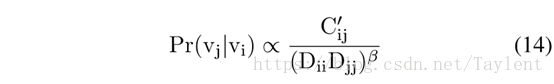AAAI 2018文章 Representation Learning for Scale-free Networks 翻译

       大三上课翻译的一篇paper，之前一直放在草稿箱，发出来供大家参考一下，没有再做修改，哪里翻译有问题或理解不对欢迎指出。

 

 

                                                            无标度网络表示学习

                                              冯瑞，杨洋，胡文杰，吴飞，庄悦婷

                                              中国浙江大学计算机科学与技术学院

                                               通讯作者：[email protected]

摘要

网络嵌入旨在保留网络的结构和固有属性的同时学习网络中顶点的低维表示。现有的网络嵌入工作主要着重于保持其微观结构，以度为1或2的顶点为例，而宏观无标度属性常常被忽略。无标度特性是现实世界网络（例如社交网络）的关键属性，它描述了顶点的度遵循重尾分布的事实（即仅有少数几个顶点的度很高）。在本文中，我们研究在学习表示无标度网络时遇到的问题。首先，通过将问题转化为高维球体填充问题（Sphere-Packing Problem），我们从理论上分析了在欧几里得空间中嵌入和重构无标度网络的困难之处。然后，我们提出了“无尺度属性”原理来设计保留网络嵌入算法的“度量惩罚”原则：即惩罚高度顶点之间的接近度。我们分别引入了光谱技术和skip-gram模型两种实现原理。在六个数据集上进行的大量实验表明，我们的算法不仅能够重构重尾分布度分布，而且还优于各种网络挖掘任务（如顶点分类和链接预测）中的最新嵌入模型。

一、介绍

由于网络能够编码丰富而复杂的数据，如人际关系和交互，网络分析已经在人工智能的许多领域吸引了大量研究者进行研究工作。 网络分析的一个主要难题是如何正确表示网络，以便保留网络结构。最直接的方法是利用邻接矩阵表示网络。但它会受到数据稀疏性的影响。其他传统的网络表示依赖于不灵活、不可扩展的手工网络特征设计（例如聚类系数），且它很耗费人力。

近年来，网络表示学习（也称为网络嵌入）已被提出并引起了可观的研究兴趣，它旨在自动将给定的网络投影到低维潜空间，并在该空间中用矢量表示每个顶点。例如，最近的一些研究应用了高级自然语言处理（NLP），其中最引人注目的是word2vec（Mikolov等，2013），网络嵌入和提出基于word2vec的算法，如DeepWalk（Perozzi，Al-Rfou和Skiena，2014）和node2vec（Grover和Leskovec2016）。此外，研究人员还将网络嵌入作为降维技术的一部分。例如，拉普拉斯特征映射（LE）（Belkin和Niyogi2003）旨在研究低维表示以扩展数据所在的流形。

图 1：真实网络的无标度特性。（a）是一个学术网络的度分布。（b）和（c）分别是基于拉普拉斯特征映射（LE）和我们提出的方法（DPWalker）学习的顶点表征重构的网络的度分布。

 

本质上，这些方法主要注重保留网络的微观结构，如顶点之间的配对关系。然而，作为网络最基本的宏观属性之一，无标度属性常常被忽略。

无标度属性描述了现实世界网络的常识：顶点的度遵循幂律分布。我们以学术网络为例，其中每条边指示顶点（研究者）是否引用了另一个顶点（研究者）至少一个的出版物。图1(a) 展示了这个网络的程度分布。对数 - 对数标度的线性表明幂律分布：当顶点的度增长时，分布的长尾大概率趋于零（Faloutsos，Faloutsos和Faloutsos 1999; Adamic和Huberman 1999）。换句话说，只有几个高度的顶点。连接到高度顶点的大部分顶点是低度的，并且不可能彼此连接。

此外，与微观结构相比，宏观无标度特性对顶点表示施加了更强的约束：在学习的潜在空间中，只有少数顶点可以接近许多其他顶点。在网络嵌入中结合无标度属性可以反映并保持真实世界网络的稀疏性，并且反过来提供有效信息以使顶点表示更具有区别性。

本文研究了在学习无标度保性能网络嵌入时遇到的问题。作为网络的表示，顶点嵌入向量预计能很好地重构网络。大多数现有算法学习在欧几里得空间中的网络嵌入。然而，我们发现大多数传统的网络嵌入算法都会高估更高的度的数量。图1(b)给出了一个例子，其中表示法是由LaplacianEigenmap研究的。我们试图从理论上分析并理解这一点，并通过将问题转化为球形填充问题来研究恢复欧几里得空间中幂律分布顶点度的可行性。通过我们的分析，我们发现，在理论上适度增加嵌入向量的维度可以帮助保持无标度属性。详情请参见第2节。

受到理论分析的启发，我们在第3节中提出了设计无标度保留网络嵌入算法的度量惩罚原则：惩罚高度顶点之间的接近度。并且会进一步介绍我们基于光谱技术（Belkin和Niyogi2003）和跳跃模型（Mikolov等，2013）实现的两个模型。如图1(c) 展示，我们的方法可以更好地保持网络的无标度属性。具体而言，得到的度分布与其理论幂律分布之间的Kolmogorov-Smirnov（又名KS统计量）距离为0.09，而由LE获得的度分布的值为0.2（越小越好）。

为了验证我们方法的有效性，我们在第4节中对合成数据和五个真实世界的数据集进行了实验。实验结果表明，我们的方法不仅能够保留网络的无标度特性，而且在不同的网络分析任务中优于最先进的嵌入算法。论文的贡献总结如下：

我们通过将问题转化为高维球体填充问题，分析了在欧氏空间中基于学习到的顶点表征来重构无标度网络的难度和可行性。

我们提出度惩罚（degree penalty）原则和两个实现来保留网络的无标度特性，并提高顶点表征的有效性。

我们通过进行大量实验来验证我们提出的原则，并发现与几个最先进的基线算法相比，我们的方法在 6 个数据集和 3 个任务上有显著提升。

二、理论分析

在本节中，我们试图研究为什么大多数网络嵌入算法会在理论上高估更高的度，并分析在欧几里得空间中是否存在无标度属性保留网络嵌入的解决方案。本节还提供了我们在第3节中展示的方法的原型。

2.1序言

符号

我们考虑一个无向网G =（V，E），其中V=｛V1，……，Vn｝是包含n个顶点的顶点集，E是边集。每个eij∈E表示vi和vj之间的无向边。我们将G的邻接矩阵定义为A = [Aij] ∈Rn×n，当eij∈ E时Aij= 1，否则Aij = 1。令D是对角矩阵，其中Dii=∑jAij是vi的度。

网络嵌入

在本文中，我们关注无向网络的表示学习。给定一个无向图G =（V，E），图嵌入问题的目的是将每个顶点vi∈V表示为一个低维空间Rk，即学习函数f：V→Un×k，其中U是嵌入矩阵，k«n和网络结构可以在U中保存。

网络重建

作为网络的表示，学习到的嵌入矩阵有望很好地重构网络。具体而言，可以基于潜在空间中的顶点之间的距离来重建网络边缘Rk。例如，vi和vj之间存在边的概率可以定义为

其中考虑了顶点vi和vj的嵌入向量ui和uj之间的欧几里得距离。在实践中，选择阈值ε∈[0,1]，并且如果pij≥ε将创建一条边eij。我们称上述方法为ε-NN，它是几何信息性的，是许多现有工作中常用的方法（Shaw和Jebara2009; Belkin和Niyogi 2003;Alanis-Lobato，Mier和Andrade- Navarro 2016）。

2.2重建无标度网络

给定一个网络，当它的顶点度数遵循幂律分布，即它只有几个高度的顶点时，我们称它为无标度网络。然而，大部分连接到高度顶点的顶点是低度的，并且不可能彼此连接。在形式上，顶点Dii的概率密度函数具有以下形式：

其中α是指数参数，C是归一化项。在实践中，上述幂律形式仅适用于度数大于某个最小值dmin的顶点（Clauset，Shalizi和Newman 2009a）。

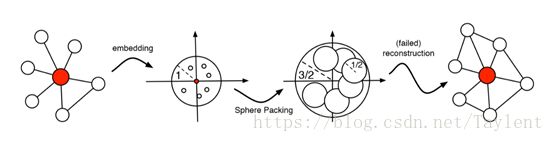
图 2：从左到右：一个以集线器顶点为中心的自我中心网络（ego-network），一个可能的嵌入解决方案（等价于一个高维球填充解决方案），但导致重构失败，其中高度顶点的数目被估计过高。

 

但是，通过ε-NN很难在欧几里得空间重建无标度网络。正如我们在图1(b)所见,更高的程度将被高估。我们打算从理论上解释这一点。

原型

当用ε-NN重建网络时，我们选择一个确定的ε，对于嵌入矢量ui的顶点vi，我们将所有落在以ui为中心、半径为ε的球中的点看作B（ui,ε），与vi连接。当vi是一个高阶顶点时，B（ui,ε）中有许多点。我们期望这些点彼此远离，保持更多的顶点和低度从而保持幂律分布。然而，事实上，因为这些点被放置在相同的闭合球B（ui，ε）中，所以更可能的式它们互相间的距离小于ε。结果就是在这些点之间会创建许多条边，这违反了无标度属性的假设。

遵循上述思想，我们在Rk中讨论了下面的一个定理，并且在不失一般性的情况下，我们将ε设置为1。

定理1（球体填充）

B（0,1）中有m个点的距离大于或等于1，当且仅当在B（0,3/2）中存在m个半径为1/2的不相交球体。

证明：B（0,3/2）中半径为1/2的任何球体的中心落在B（0,1）中，并且两个半径为1/2的不同球体的任何两个中心之间的距离大于或等于1

备注

定理1 将无标度网络重建的问题转换为球形填充问题，该问题试图在高维空间中找到球体的最佳包装（Cohn和Elkies2003; Vance 2011;Venkatesh 2012）。图2 举一个例子，以高度顶点为中心的网络嵌入到二维空间。嵌入结果对应到一个等效的球形包装解决方案，它不能放置足够的不相交的球体并导致失败的网络Rk中的填充密度为Δk，这意味着Rk中的球的填充达到大于Δk的填充密度。

根据定理1，我们的目标是找到一个密度较大的包装解决方案，这样封闭球体中的更多点可以保持其距离大于1。但是，在一般情况下，找到最佳包装密度仍是一个悬而未决的问题。尽管如此，我们仍能够得出足够大的k的Δk的上下界。

定理2（Δk的上下界）

具体来说，我们有

下面的不等式适用于足够大的k：

式4是k≥115时最好的上界之一（Cohn and Zhao 2014）。上述定理的证明可以在Kabatiansky和Levenshtein理论中找到。

定理3

假设x在Rk中，ε> 0，并且B（x，ε）中至多有Mk个点，它们之间的距离大于ε，则

⌊ ⌋意思是取整数部分。上限足够大

证明：按定理1我们只需要估计可以在B（x，ε）中拟合的半径为ε的不相交球体的数量。一个半径为R的k维球体的体积可以由得到。在半径内，B（x，ε）为球心和ε为半径，体积为V1=V2=。

由于最优填充密度和Δk有关，我们有：

将等式3和4带入就可以得到我们想要的结果。

讨论

等式5中Mk的下界在嵌入向量的维数k足够大时，在欧几里得空间中提出利用ε-NN重构无尺度网络的可行性。例如，当k = 100时，我们有Mk>4.061017，这足以保持大多数真实世界网络的无标度属性。

三、我们的方法

大概的概念

受到我们理论分析的启发，我们提出了一种度量惩罚原则，用于设计无标度属性保留嵌入算法：在保留一阶和二阶接近度的同时，高度顶点之间的接近度将受到惩罚。我们在下面给出这个原则的总体思路。

无标度特性的特征是无处不在的“大型枢纽”：它吸引了网络中的大部分优势。大多数现有网络嵌入算法明确或隐含地试图通过保持一阶和/或二阶邻近来使这些大型集线器相互靠近，（Belkin and Niyogi 2003;Tang etal.2015;Perozzi,Al-Rfou,and Skiena 2014）但是，连接到大型集线器并不意味着其接近性与连接具有中等度的顶点一样强。以社交网络为例，一位名人可能会收获一群粉丝。然而，名人可能并不熟悉她的粉丝此外，同一名人的两名追随者可能完全不相识，也可能完全不一样。作为比较，一个平庸的用户更可能知道并且与她的追随者相似。

从另一个角度来看，高度顶点vi更可能伤害无标度属性，因为将更多不相交的球体放置在闭合球中更困难（第2节）

程度惩罚原则可以通过各种方法实现。在本文中，我们基于我们的原理引入了两个建议模型，分别是基于光谱技术和skip-gram模型实现。

3.1模型I：DP-Spectral

我们的第一个模型，基于程度罚分的谱嵌入（DP-Spectral），主要利用图谱技术。给定一个网络G =（V，E）及其邻接矩阵A，我们定义一个矩阵C来表示G中任意两个顶点的公共邻居：

其中Cij是vi和vj的共同邻居的数量。C也可以被看作是二阶近似的度量，并且可以容易地扩展以进一步考虑一阶近似：

我们的目标是模拟我们的顶点度的影响模型，我们进一步扩展C´以考虑度的惩罚：

其中β∈R是用来表示程度惩罚强度的模型参数，D是对角矩阵，其中Dii是vi的度。因此W与C´成正比，并且与顶点度成反比。

目的

我们的目标是学习顶点表示U，其中ui∈Rk是U的第i行,代表顶点vi的嵌入向量，并且最小化

 

约束为：

 

等式10保证了嵌入向量不会塌陷到维度小于k的子空间上（Belkin and Niyogi 2003）。

优化

为了最小化等式9，我们利用图拉普拉斯算子，这与多元微积分中的拉普拉斯算子类似。在形式上，我们定义图拉普拉斯L如下所示：

观察一下

期望的U最小化目标函数（9）通过下式获得

其中ti是L的一个特征向量。实际上，我们使用W和L的归一化形式（即D-1/2WD1/2和I-D-1/2WD1/2）。

3.2模型II：DP-Walker

我们的第二种方法，基于DP-Walker的度惩罚，使用skip-gram模型word2vec。

我们首先简单描述word2vec模型及其在网络嵌入任务上的应用。给定一个文本语料库，Mikolov et al提出word2vec通过对其上下文的进行预测来学习每个单词的表达。受它的启发，一些像DeepWalk这样的网络嵌入算法（Perozzi，Al-Rfou和Skiena，2014）和node2vec（Grover和Leskovec2016）通过在随机游走生成的路径中共同出现的顶点“上下文”定义一个顶点。

具体来说，随机游走是根据顶点Vi是的一个随机过程，k = 1，……，m。其中是从的邻接顶点抽样出的一个顶点，m是路径长度。传统方法将P（|）视为均匀分布的，的每个邻接顶点都有相等的概率被抽样。然而，正如我们提出的度惩罚原则所表明的，高度的顶点vj的邻居vi可能与vj不相似。换句话说，vj应该不太可能被抽样为vi的上下文之一。因此，我们定义随机游走从vi跳到vj的概率为

C´可以在等式7中找到，β是模型参数。根据等式14，我们发现当vj具有更多共同邻居并且具有更低的度时，vj将有更大的抽样机会。在获得随机游走生成的路径之后，我们通过预测每个顶点的上下文来使skip-gram能够学习G的有效顶点表示。

这会导致优化问题

其中2 w是我们考虑的路径长度。具体而言，对于每个随机游走，我们将其馈送到skip-gram算法（Mikolov等，2013）去更新顶点表示。为了实现，我们使用Hierarchical Soft-max（Morin和Bengio2005;Mnih和Hinton 2009）来估计相关的概率分布。

四、实验

4.1实验设置

数据集

我们使用四个数据集，统计数据汇总在表中1 进行评估。

  Synthetic：我们通过优先附件模型生成合成数据集（Vazquez 2003），其中描述了无标度网络的生成。

   Facebook（Leskovec和Mcauley，2012）：这个数据集是Facebook的子网1顶点表示Facebook的用户，边缘表示用户之间的友谊。

   Twitter（Leskovec和Mcauley，2012）：这个数据集是Twitter的子网2，其中顶点表示Twitter的用户，并且边缘表示以下关系。

  Coauthor（Leskovec，Kleinberg和Faloutsos2007）：该网络涵盖作者之间的科学合作。顶点是作者。如果两位作者至少合作了一篇论文，则存在无向边。

  Ciatation（Tang等2008）：与共同作者类似，这也是一个学术网络，顶点是作者。边缘表示引用而不是共同作者的关系。

  Mobile：这是由PPDai提供的移动网络3。顶点是PPDai注册用户。两个用户之间的边缘表示其中一个用户已经呼叫另一个用户。总的来说，它包含超过一百万个呼叫日志。

基线方法

我们在实验中比较了以下四种网络嵌入算法：

  拉普拉斯特征映射（LE）（Belkin和Niyogi 2003）：这代表了基于频谱的网络嵌入算法。它旨在学习低维表示以扩展数据所在的流形。

表 1：数据集的统计数字。|V| 表示顶点的数量，|E| 表示边的数量。

  DeepWalk （Perozzi，Al-Rfou和Skiena，2014）：这代表基于skip-gram模型的网络嵌入算法。它首先在网络上生成随机游走，并通过路径中共同出现的顶点来定义顶点的上下文。然后，通过预测每个顶点的上下文来学习顶点表示。具体来说，我们从每个顶点开始进行10次随机游走，每次随机游走的长度为40。

  DP-Spectral：这是一种基于光谱技术实现我们的度数惩罚原理。

   DP-Walker：这是我们方法的另一个实现。 它基于skip-gram模型。

除非另有说明，否则我们实验的嵌入维数为200。

任务

我们首先利用不同的算法来学习某个数据集的顶点表示，然后将学习的嵌入应用于三个不同的任务：

  网络重构：此任务旨在验证算法是否能够保留网络的无标度属性。我们通过重建度和给定网络中的度之间的相关系数来评估不同算法的性能。

  链接预测：给定两个顶点vi和vj，我们将它们的嵌入向量ui和uj馈送到线性回归分类器，并确定vi和vj之间是否存在边。具体来说，我们使用ui -uj作为特征，并随机选择约1％的顶点对进行训练和评估。

  顶点分类：在这个任务上，我们考虑顶点标签。例如，在引文中，每个顶点都有一个标签来指示研究人员的研究领域。具体来说，给定一个顶点vi，我们定义它的特征向量为ui，并训练一个线性回归分类器来确定它的标签。

4.2网络重建

比较结果

在这个任务中，在获得顶点表示之后，我们使用第2节中介绍的ε-NN算法重建网络。然后，我们通过考虑重建度和原始度的三个不同相关系数来评估不同方法在重构幂律分布顶点度方面的性能：皮尔逊系数（Shao 2007），斯皮尔曼系数（Spearman 1904）和肯德尔系数（Kendall 1938）。所有这些统计数据都用于评估配对样本之间的某些关系。皮尔逊系数用于检测线性关系，而斯皮尔曼系数和肯德尔系数能够找到单调关系。

为了选择ε，对于每个算法，我们将步骤0.01中的所有ε范围从0.01变为1，并选择价值最大化原始和恢复程度之间的皮尔逊相关系数。我们选择皮尔逊系数作为评估指标是因为度分布的无标度特性。

图 3：模型参数分析。（a）和（b）分别展示了合成数据集和 Facebook 数据集中嵌入维度 k 的敏感性。（c）和（d）表示度惩罚参数 β 的敏感性。由于空间限制，我们忽略了其它数据集上的结果。

 

数据集	方法模型()	皮尔逊系数	斯皮尔曼系数	肯德尔系数
Synthetic	LE(0.55)	0.14	0.054	0.039
	DeepWalk(0.91)	0.47	-0.22	-0.18
	DP-Spectral(0.52)	0.92	0.79	0.63
	DP-Walker(0.95)	0.94	0.63	0.52
Facebook	LE(0.52)	0.48	0.18	0.12
	DeepWalk(0.81)	0.73	0.65	0.49
	DP-Spectral(0.52)	0.87	0.67	0.51
	DP-Walker(0.84)	0.75	0.73	0.57
Twitter	LE(0.81)	0.17	0.19	0.17
	DeepWalk(0.51)	0.08	0.21	0.26
	DP-Spectral(0.93)	0.50	0.34	0.27
	DP-Walker(0.087)	0.40	0.33	0.27
Coauthor	LE(0.50)	0.32	0.04	0.03
	DeepWalk(0.92)	0.66	0.31	0.25
	DP-Spectral(0.51)	0.64	0.69	0.55
	DP-Walker(0.93)	0.75	0.44	0.35
Citation	LE(0.99)	0.11	-0.27	-0.20
	DeepWalk(0.97)	0.51	0.28	0.20
	DP-Spectral(0.50)	0.45	0.72	0.54
	DP-Walker(0.98)	0.62	0.65	0.50
Mobile	LE(0.51)	0.10	0.05	0.04
	DeepWalk(0.71)	0.77	0.22	0.20
	DP-Spectral(0.50)	0.40	0.68	0.60
	DP-Walker(0.78)	0.93	0.22	0.20

 

表2：不同方法在无标度房地产重建中的表现。对于每种方法，选择ε（在相应方法之后指示）以使皮尔逊系数最大化。

从表2，我们看到我们的算法显着优于基线。尤其是，DP-Walker的皮尔逊系数达到了至少44.5％的提升，而DP-Spectral的皮尔逊系数达到了至少84.3％的提升。我们的算法重建的顶点度的良好适应性表明我们可以更好地保持网络的无标度属性。此外，我们看到最大化皮尔逊系数用于DP-Spectral的ε比其他方法更稳定（即约0.51）。因此可以在实践中更容易地调整DP-Spectral的参数。

保持无标度属性

重建后网络，对于每个嵌入算法，我们通过拟合重建度分布来验证其有效性以保持无标度属性（例如，图1(b) 和（c））到理论幂律分布（Alstott，Bull- 更多，Plenz2014）。然后，我们计算这两个分布之间的Kolmogorov-Smirnov距离，发现所提出的方法总是可以获得比基线更好的结果（平均为0.115 vs 0.225）。

参数分析

我们进一步研究了模型参数的敏感性：嵌入维数和度数惩罚权重β。由于空间限制，我们仅在Synthetic和Facebook上提供结果并省略其他结果。图3（c）和3(b) 显示了我们的算法在不同嵌入维数下得到的Pearson相关系数。当嵌入维度增长时，性能显着增加。这些数字表明，将网络嵌入欧几里得空间时，存在足以保持无标度特性的维度，并且进一步增加嵌入维度的效果有限。如图所示，随着尺寸的增加，DP-Walker的相关性不会发生显着变化。这些数字还表明，DP-Walker即使在较低维度下也能够获得相当高的Pearson相关性，并且它需要比DP-Spectral低的嵌入维度才能获得满意的性能。

我们也研究β如何影响性能。 图3(c) 和3(d) 显示DP-Spectral对β的选择更敏感。 这主要是由于在DP-Spectral中，β的影响表现在目标函数（等式9), 这比采样过程中体现的DP-Walker中的DP-Walker更受限制。图3（c）和3（d）表明β的最优选择随图形而变化。这是有道理的，因为β可以看作是对度的惩罚，因此β的影响据说与原始网络的拓扑有关。

4.3链接预测

在此任务中，我们考虑以下评估指标：查准率（Pearson）、查全率（Spearman）和F1分数。表3 演示了链接预测任务中不同方法的性能。对于我们的方法，我们使用表格中优化的模型参数β。我们看到，在大多数情况下，DP-Spectral获得性能最好，这表明在所提出的原理的帮助下，我们不仅可以保持网络的无标度特性，还可以提高嵌入向量的有效性。

 

数据集	方法模型	查准率	查全率	F1
Synthetic	LE	0.52	0.53	0.53
	DeepWalk	0.51	0.51	0.51
	DP-Spectral	0.64	0.68	0.66
	DP-Walker	0.61	0.63	0.62
Facebook	LE	0.75	0.92	0.83
	DeepWalk	0.84	0.97	0.90
	DP-Spectral	0.76	0.98	0.85
	DP-Walker	0.82	0.95	0.89
Twitter	LE	0.58	0.35	0.43
	DeepWalk	0.65	0.77	0.70
	DP-Spectral	0.59	0.98	0.73
	DP-Walker	0.54	0.58	0.56
Coauthor	LE	0.61	0.83	0.70
	DeepWalk	0.55	0.58	0.56
	DP-Spectral	0.62	0.89	0.73
	DP-Walker	0.56	0.66	0.61
Citation	LE	0.54	0.56	0.55
	DeepWalk	0.54	0.56	0.55
	DP-Spectral	0.52	0.99	0.68
	DP-Walker	0.55	0.57	0.56
Mobile	LE	0.75	0.36	0.48
	DeepWalk	0.55	0.60	0.57
	DP-Spectral	0.63	0.89	0.74
	DP-Walker	0.54	0.58	0.56

表3：链路预测的实验结果。

表4：多分类任务的准确性。 标签分别代表架构，计算机网络，计算机科学，数据挖掘，理论，图形和未知。

 

4.4顶点分类

表4 列出引文的顶点分类任务的准确性。我们的任务是确定作者的研究领域，这是一个多分类问题。我们将特征定义为由四种不同的嵌入算法获得的顶点表示。一般来说，从表格中我们可以看到DP-Walker和DP-Spectral分别击败Deepwalk和Laplacian Eigenmap。 特别是，DP-Spectral在7个标签中有5个达到最佳效果。此外，我们也可以观察其表现的稳定性。DP-Spectral在所有标签上的结果比其他方法更稳定。相比之下，LE对于两个标签取得了令人满意的结果，但对于其他标签而言，结果可能较差。具体而言，DP-Spectral的标准偏差为0.04，而LE为0.26，DeepWalk为0.1。

五、相关工作

网络嵌入

网络嵌入旨在学习给定网络中顶点的表示。一些研究人员将网络嵌入作为降维技术的一部分。例如，拉普拉斯特征映射（LE）（Belkin和Niyogi 2003）旨在学习顶点表示以扩展数据所在的流形。作为LE的变体，局部保持投影（LPP）（He et al.2005）学习从特征空间到嵌入空间的线性投影。 此外，还有其他线性（Jol- liffe 2002）和非线性（Tenenbaum，DeSilva和Lang- ford 2000）网络嵌入算法降维。最近的网络嵌入工作在自然语言处理方面取得了进展，其中最著名的模型是word2vec（Mikolov等，2013），学习单词的分布式表示。基于word2vec，Perozzi等人通过在随机游步路径中的同现来定义顶点的“上下文”（Perozzi，Al-Rfou，和Skiena 2014）。最近，Grover等人提出了基于宽度优先搜索和基于广度优先搜索的过程的混合来生成顶点路径（Grover和Leskovec2016）。董等人进一步开发处理异构网络的模型（Dong，Chawla和Swami 2017）。 线（Tang等，2015）将顶点的上下文分解为一阶（邻居）和二阶（两度邻居）邻近。Wang等人 在他们的顶点表示中保存社区信息（Wang et al.2017）。然而，上述所有方法都着眼于保留微观网络结构并忽略网络的宏观无标度特性。

无标度网络

无标度属性已被发现在各种网络系统中无处不在（Mood 1950; Newman 2005; Clauset，Shalizi和Newman 2009b），如互联网自治系统图（Faloutsos，Faloutsos and Faloutsos 1999），互联网路由器图（Govindan and Tangmunarunkit 2000），万维网子集的度分布（Barabasi and Albert1999）。新人提供了这些工作的全面清单（Newman2005）。然而，调查低维向量空间中的无标度特性并建立其与网络嵌入的合作尚未得到充分考虑。

六、结论

在本文中，我们研究了学习无标度保留网络嵌入时遇到的问题。我们首先分析在欧几里得空间中基于学习的顶点表示重构无标度网络的可行性，将我们的问题转换为球体包装问题。然后我们提出度量惩罚原则作为我们的解决方案，并分别利用频谱技术和skip-gram模型引入两种实现。提出的原则也可以使用其他方法来实现，这些方法留作我们未来的工作。最后，我们对合成数据和五个真实世界数据集进行了广泛的实验，以验证我们方法的有效性。

致谢

这项工作得到了中央大学基础研究基金，973计划（2015CB352302），国家自然科学基金委（U1611461，61625107,61402403），浙江省重点项目（2015C01027）。

 

 

参考文献

[Adamicand Huberman 1999] Adamic, L., and Huberman, B. A. 1999. The nature of marketsin the world wide web. Q. J. Econ.

[Alanis-Lobato,Mier, and Andrade-Navarro 2016] AlanisLobato, G.; Mier, P.; andAndrade-Navarro, M. A. 2016. Effcient embedding of complex networks tohyperbolic space via their laplacian. In Scientific reports.

[Alstott,Bullmore, and Plenz 2014] Alstott, J.; Bullmore, E.; and Plenz, D. 2014.powerlaw: A Python Package for Analysis of Heavy-Tailed Distributions. PLoS ONE9:e85777.

[Barab´asi and Albert 1999]Barab´asi, A.-L., and Albert, R. 1999. Emergence of scaling in random networks.science 286(5439):509–512.

[Belkinand Niyogi 2003] Belkin, M., and Niyogi, P. 2003. Laplacian eigenmaps fordimensionality reduction and data representation. Neural Comput.15(6):1373–1396.

[Clauset,Shalizi, and Newman 2009a] Clauset, A.; Shalizi, C. R.; and Newman, M. E. J.2009a. Power-law distributions in empirical data. SIAM Review 51(4):661–703.

[Clauset,Shalizi, and Newman 2009b] Clauset, A.; Shalizi, C. R.; and Newman, M. E.2009b. Power-law distributions in empirical data. SIAM review 51(4):661–703.

[Cohnand Elkies 2003] Cohn,H.,andElkies,N. 2003. New upper bounds on sphere packingsi. Annals of Mathematics 689–714.

[Cohnand Zhao 2014] Cohn,H.,andZhao,Y. 2014. Sphere packing bounds via sphericalcodes. Duke Mathematical Journal 163(10):1965–2002.

[Dong,Chawla, and Swami 2017] Dong, Y.; Chawla, N.; andSwami,A. 2017.metapath2vec:Scalablerepresentation learningforheterogeneousnetworks. InKDD’17,135–144.

[Faloutsos,Faloutsos, and Faloutsos 1999] Faloutsos, M.; Faloutsos, P.; and Faloutsos, C.1999. On power-law relationships of the internet topology. In COMPUT COMMUNREV, volume 29, 251–262.

[Govindanand Tangmunarunkit 2000] Govindan, R., and Tangmunarunkit, H. 2000. Heuristicsfor internet map discovery. In INFOCOM’00, volume 3, 1371–1380.

[Groverand Leskovec 2016] Grover, A., and Leskovec, J. 2016. node2vec: Scalablefeature learning for networks. In KDD’16, 855–864.

[Heet al. 2005] He, X.; Yan, S.; Hu, Y.; Niyogi, P.; and Zhang, H. 2005. Facerecognition using laplacianfaces.IEEETransactionsonPatternAnalysisandMachineIntelligence 27(3):328–340.

[Jolliffe2002] Jolliffe, I. 2002. Principal component analysis. Wiley Online Library.

[Kabatianskyand Levenshtein 1978] Kabatiansky, G. A., and Levenshtein, V. I. 1978. Onbounds for packings on a sphere and in space. Problemy Peredachi Informatsii14(1):3–25.

[Kendall1938] Kendall,M.G. 1938. Anewmeasureofrank correlation. Biometrika30(1/2):81–93. [Leskovec and Mcauley 2012] Leskovec, J., and Mcauley, J. 2012.Learning to discover social circles in ego networks. In NIPS’12, 539–547.

[Leskovec,Kleinberg, and Faloutsos 2007] Leskovec, J.; Kleinberg, J. M.; and Faloutsos,C. 2007. Graph evolution: Densification and shrinking diameters. ACMTransactions on Knowledge Discovery From Data 1(1):2.

[Mikolovet al. 2013] Mikolov, T.; Chen, K.; Corrado, G.; and Dean, J. 2013. Efficient estimation of word representations in vector space. In NIPS’13, 3111–3119.

[Mnihand Hinton 2009] Mnih, A., and Hinton, G. E. 2009. A scalable hierarchicaldistributed language model. In Koller, D.; Schuurmans, D.; Bengio, Y.; andBottou, L., eds., Advances in Neural Information Processing Systems 21. CurranAssociates, Inc. 1081–1088.

[Mood1950] Mood, A. M. 1950. Introduction to the theory of statistics.

[Morinand Bengio 2005] Morin, F., and Bengio, Y. 2005. Hierarchical probabilisticneural network language model. In AISTATS05, 246–252.

[Newman2005] Newman, M. E. 2005. Power laws, pareto distributions and zipf’s law.Contemporary physics 46(5):323–351.

[Perozzi,Al-Rfou, and Skiena 2014] Perozzi, B.; Al-Rfou, R.; and Skiena, S. 2014.Deepwalk: Online learning of social representations. In KDD’14, 701–710.

[Shao2007] Shao, J. 2007. Mathematical Statistics. Springer, 2 edition.

[Shawand Jebara 2009] Shaw, B., and Jebara, T. 2009. Structure preserving embedding.In Proceedings of the 26th Annual International Conference on Machine Learning,ICML ’09, 937–944. New York, NY, USA: ACM.

[Spearman1904] Spearman, C. 1904. The proof and measurement of association between twothings. The American Journal of Psychology 15(1):72–101.

[Tanget al. 2008] Tang, J.; Zhang, J.; Yao, L.; Li, J.; Zhang, L.; and Su, Z. 2008.Arnetminer: extraction and mining of academic social networks. In KDD’08,990–998.

[Tanget al. 2015] Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; and Mei, Q. 2015.Line: Large-scale information network embedding. In WWW’15, 1067–1077.

[Tenenbaum,De Silva, and Langford 2000] Tenenbaum, J. B.; De Silva, V.; and Langford, J.C. 2000. A global geometric framework for nonlinear dimensionality reduction.science 290(5500):2319–2323.

[Vance2011] Vance, S. 2011. Improved sphere packing lowerboundsfromhurwitzlattices.AdvancesinMathematics 227(5):2144–2156.

[Vazquez2003] Vazquez, A. 2003. Growing network with local rules: Preferentialattachment, clustering hierarchy, and degree correlations. Physical Review E67(5):056104.

[Venkatesh2012] Venkatesh, A. 2012. A note on sphere packings in high dimension.International mathematics research notices 2013(7):1628–1642.

[Wanget al. 2017] Wang, X.; Cui, P.; Wang, J.; Pei, J.; Zhu, W.; and Yang, S. 2017.Community preserving network embedding. In AAAI’17.

 

感谢阅读。