多智能体强化学习入门(一)——基础知识与博弈
一、引言
在多智能体系统中,每个智能体通过与环境进行交互获取奖励值(reward)来学习改善自己的策略,从而获得该环境下最优策略的过程就多智能体强化学习。
在单智能体强化学习中,智能体所在的环境是稳定不变的,但是在多智能体强化学习中,环境是复杂的、动态的,因此给学习过程带来很大的困难。
- 维度爆炸:在单体强化学习中,需要存储状态值函数或动作-状态值函数。在多体强化学习中,状态空间变大,联结动作空间(联结动作是指每个智能体当前动作组合而成的多智能体系统当前时刻的动作,联结动作 , 指第i个智能体在时刻t选取的动作。)随智能体数量指数增长,因此多智能体系统维度非常大,计算复杂。
- 目标奖励确定困难:多智能体系统中每个智能体的任务可能不同,但是彼此之间又相互耦合影响。奖励设计的优劣直接影响学习到的策略的好坏。
- 不稳定性:在多智能体系统中,多个智能体是同时学习的。当同伴的策略改变时,每个智能体自身的最优策略也可能会变化,这将对算法的收敛性带来影响。
- 探索-利用:探索不光要考虑自身对环境的探索,也要对同伴的策略变化进行探索,可能打破同伴策略的平衡状态。每个智能体的探索都可能对同伴智能体的策略产生影响,这将使算法很难稳定,学习速度慢。
在多智能体系统中智能体之间可能涉及到合作与竞争等关系,引入博弈的概念,将博弈论与强化学习相结合可以很好的处理这些问题。
二、博弈论基础
在本节中主要介绍多智能体强化学习中需要用到的一些概念及定义,仅局限于多智能体强化学习算法的理解分析。包括矩阵博弈、静态博弈、阶段博弈、重复博弈和随机博弈等概念。
1. 矩阵博弈
一个矩阵博弈可以表示为 ,n表示智能体数量, 是第i个智能体的动作集, 表示第i个智能体的奖励函数,从奖励函数可以看出每个智能体获得的奖励与多智能体系统的联结动作有关,联结动作空间为 。每个智能体的策略是一个关于其动作空间的概率分布,每个智能体的目标是最大化其获得的奖励值。
令 表示智能体i在,联结策略 下的期望奖励,即值函数。
定义1:纳什均衡
在矩阵博弈中,如果联结策略 满足
则为一个纳什均衡。
总体来说,纳什均衡就是一个所有智能体的联结策略。在纳什均衡处,对于所有智能体而言都不能在仅改变自身策略的情况下,来获得更大的奖励。
定义 表示在执行联结动作 时,智能体i所能获得的期望奖励。令 表示第i个智能体选取动作 的概率。则纳什均衡的另一种定义方式如下
定义2:严格纳什均衡
若(1)式严格大于,则 为严格纳什均衡。
定义3:完全混合策略
若一个策略对于智能体动作集中的所有动作的概率都大于0,则这个策略为一个完全混合策略。
定义4:纯策略
若智能体的策略对一个动作的概率分布为1,对其余的动作的概率分布为0,则这个策略为一个纯策略。
2. 两个智能体的矩阵博弈中的纳什均衡
本节介绍针对一个两智能体博弈问题的常规建模方式,并介绍几种常见的博弈形式。后面的很多多智能体强化学习算法都是以此为基础建立起来的,双智能体矩阵博弈对于多智能体强化学习类似于感知机对于神经网络。
在双智能体矩阵博弈中,我们可以设计一个矩阵,矩阵每一个元素的索引坐标表示一个联结动作 ,第i个智能体的奖励矩阵 的元素 就表示第一个智能体采用动作x,第二个智能体采用动作y时第i个智能体获得的奖励。通常我们将第一个智能体定义为行智能体,第二个智能体定义为列智能体,行号表示第一个智能体选取的动作,列号表示第二个智能体选取的动作。则对于只有2个动作的智能体,其奖励矩阵分别可以写为
定义5. 零和博弈
零和博弈中,两个智能体是完全竞争对抗关系,则 。在零和博弈中只有一个纳什均衡值,即使可能有很多纳什均衡策略,但是期望的奖励是相同的。
定义6. 一般和博弈
一般和博弈是指任何类型的矩阵博弈,包括完全对抗博弈、完全合作博弈以及二者的混合博弈。在一般和博弈中可能存在多个纳什均衡点。
我们定义策略 为智能体i的动作集中每个动作的概率集合, 表示可选的动作数量,则值函数 可以表示为
纳什均衡策略 可以表示为
表示第 个智能体的策略空间, 表示另一个智能体。
如上定义一个两智能体一般和博弈为
若满足
则$l,f$为纯策略严格纳什均衡, 表示除了 的另一个策略。
3. 线性规划求解双智能体零和博弈
求解双智能体零和博弈的公式如下
上式的意义为,每个智能体最大化在与对手博弈中最差情况下的期望奖励值。
将博弈写为如下形式
定义 表示第一个智能体选择动作 的概率, 表示第二个智能体选择动作 的概率。则对于第一个智能体,可以列写如下线性规划
同理,可以列出第二个智能体的纳什策略的线性规划
求解上式就可得到纳什均衡策略。
4. 几个博弈概念
马尔可夫决策过程包含一个智能体与多个状态。矩阵博弈包括多个智能体与一个状态。随机博弈(stochastic game / Markov game)是马尔可夫决策过程与矩阵博弈的结合,具有多个智能体与多个状态,即多智能体强化学习。为更好地理解,引入如下定义
静态博弈:static/stateless game是指没有状态s,不存在动力学使状态能够转移的博弈。例如一个矩阵博弈。
阶段博弈:stage game,是随机博弈的组成成分,状态s是固定的,相当于一个状态固定的静态博弈,随机博弈中的Q值函数就是该阶段博弈的奖励函数。若干状态的阶段博弈组成一个随机博弈。
重复博弈:智能体重复访问同一个状态的阶段博弈,并且在访问同一个状态的阶段博弈的过程中收集其他智能体的信息与奖励值,并学习更好的Q值函数与策略。
多智能体强化学习就是一个随机博弈,将每一个状态的阶段博弈的纳什策略组合起来成为一个智能体在动态环境中的策略。并不断与环境交互来更新每一个状态的阶段博弈中的Q值函数(博弈奖励)。
对于一个随机博弈可以写为 ,其中n表示智能体数量,S表示状态空间, 表示第i个智能体的动作空间, 表示状态转移概率, 表示第i个智能体在当前状态与联结动作下获得的回报值, 表示累积奖励折扣系数。随机博弈也具有马尔科夫性,下一个状态与奖励只与当前状态与当前的联结动作有关。
对于一个多智能体强化学习过程,就是找到每一个状态的纳什均衡策略,然后将这些策略联合起来。 就是一个智能体i的策略,在每个状态选出最优的纳什策略。多智能体强化学习最优策略(随机博弈的纳什均衡策略)可以写为 ,且 满足
为 折扣累积状态值函数,用 简记上式。用 表示动作状态 折扣累积值函数,在每个固定状态s的阶段博弈中,就是利用 作为博弈的奖励求解纳什均衡策略的。根据强化学习中的Bellman公式,可得
MARL(多智能体强化学习)的纳什策略可以改写为
根据每个智能体的奖励函数可以对随机博弈进行分类。若智能体的奖励函数相同,则称为完全合作博弈或团队博弈。若智能体的奖励函数逆号,则称为完全竞争博弈或零和博弈。为了求解随机博弈,需要求解每个状态s的阶段博弈,每个阶段博弈的奖励值就是 。
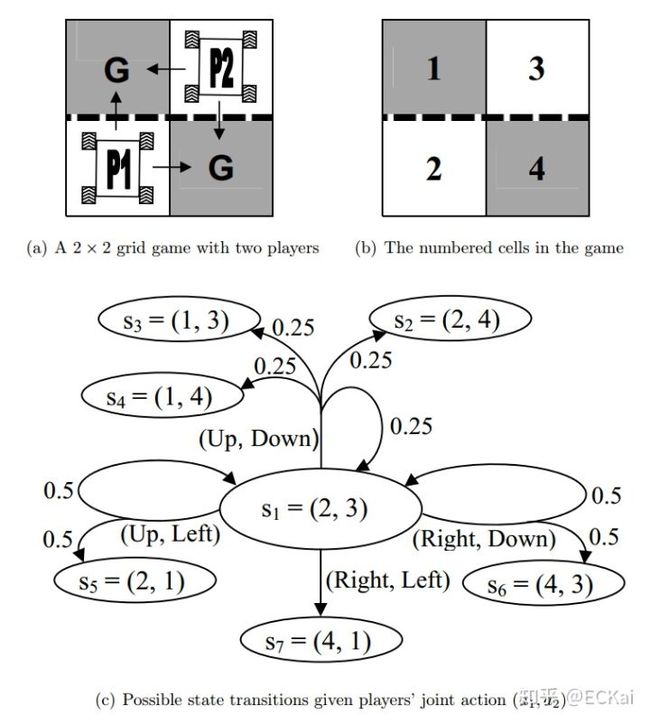
三、随机博弈示例
定义一个2*2的网格博弈,两个智能体分别表示为 , ,1的初始位置在左下角,2的初始位置在右下角,每一个智能体都想以最快的方式达到G标志的地方。从初始位置开始,每个智能体都有两个动作可以选择。只要有一个智能体达到G则游戏结束,达到G的智能体获得奖励10,奖励折扣率为0.9。虚线表示栏杆,智能体穿过栏杆的概率为0.5。该随机博弈一共包含7个状态。这个博弈的纳什均衡策略是,每个智能体到达邻居位置而不穿过栏杆。
根据前文公式,我们可以得到如下状态值函数
由此我们可以得到动作状态值函数
求解上述矩阵博弈就可得到多智能体强化学习的策略。