随机过程基础(6)--应用随机过程分析音乐（语音）信号（1）、随机序列功率谱（PSD）

随 机 序 列 功 率 谱

概念

对于平稳随机序列X(n)，如果相关函数满足
$$\sum _{m=-\infty }^{+\infty }|R_X(m)|<\infty$$
那么它的功率谱定义为自相关函数$R_X(m)$的傅里叶变换：
$$G_X(e^{j\omega })=\sum _{m=-\infty }^{+\infty }|R_X(m)|e^{-jm\omega }$$
对于功率有限的平稳随机序列，它的自相关函数可以用功率谱表示：
$$R_X(m)=\frac{1}{2\pi }{\int }_{-\pi }^{+\pi }{G}_X(e^{j\omega })e^{jm\omega }d\omega$$
简单表示起见，$G_X(e^{j\omega })$简记为$G_X(\omega )$。显然，功率谱密度是周期为2pi的周期函数。同样地，复习一下离散傅里叶变换的导出。它与连续傅里叶变换同理，但是难理解一些。

离散傅里叶变换基础知识

离散傅里叶级数的导出

当满足奈奎斯特抽样定理时，信号f(t)的抽样信号f_s(t)包含着全部谱信息，（通过低通滤波器后）可无失真恢复f(t)。（也就是表征f(t)的全部频域特性）
离散时间虚指数信号是周期信号的充要条件。说人话，假如
$$x(n)=e^{jn\omega }$$是周期为N的离散时间信号，则
$$x(n)=e^{jn\omega }=x(n+N)=e^{j(n+N)\omega }$$导出
$$e^{jn\omega }(1-e^{jN\omega })=0$$导出
$$N\omega =2\pi m，\omega =2\pi \frac{m}{N}$$
m为整数，则m/N 为有理数。这表明，周期为N的离散时间信号x(n)的角频率必须是\pi的有理数倍。否则，$x(n)=e^{jn\omega }$不是周期信号。而连续时间周期信号对角频率无要求，可为任意实数。
设$x(n)=e^{j\omega n}$是周期为N的信号，那么任意$\Delta \omega =2m\pi ,m\in Z$在整个$n\in (-\infty ,\infty )$上：
$$x(n)=e^{j\omega n}=e^{j(\omega +\Delta \omega )n}=e^{j(\omega +2\pi m)n}$$
这表明，角频率为$\omega$和$\omega +2\pi m$的离散时间虚指数周期信号完全相同。离散时间虚指数信号可看做连续时间虚指数信号的采样，在给定采样率${\omega }_s$的情况下，x(n)可能来自频率为w的连续时间虚指数信号，也可能来自w+2nw_s的连续时间虚指数信号，呈现特殊的频域周期性。

从周期信号f_T（t）到f_s(t)的抽样系统是线性时变系统，其输出信号f_s（t）可以表示为f_T(t)的傅里叶级数展开各项的抽样后相加。
$$f_T(t)=\sum _{k=-\infty }^{+\infty }{F}_k{e}^{jk\Omega n\Delta T}=\sum _{-\infty }^{\infty }{F}_k{e}^{jk\frac{2\pi }{T}n\Delta T}$$
若$\frac{\Delta T}{T}=\frac{1}{N}$则
$$x(n)=\sum _{k=-\infty }^{\infty }{F}_k{e}^{jkn\frac{2\pi }{N}}$$
那就可以看出，只要$\frac{\Delta T}{T}$是2pi的有理数倍，采样后的信号即使周期信号。（基频$\Omega$可以是任意实数）
观察$x(n)={\sum }_{k=-\infty }^{\infty }{F}_k{e}^{jkn\frac{2\pi }{N}},-\infty <n<\infty$可以看出它已经很像傅里叶级数了。而且，对于任意的n：
$$e^{j2\pi kn/N}=e^{j2\pi (k+N)n/N}$$
既然前后周期（N）之间都相等了，那关于k求和时，无限项经合并同类项后，只剩下N项：
$$x(n)=\sum _{k=-\infty }^{\infty }{F}_k{e}^{jkn\frac{2\pi }{N}}=\sum _{k=0}^{N-1}{a}_k{e}^{j2\pi kn/N}=x(n)$$
其中，
$$a_k=\sum _{m=-\infty }^{\infty }{F}_{k+mN},k\in 0,1,...,N-1$$

正式的离散周期信号傅里叶级数展开：
$$x(n)=\sum _{k=0}^{N-1}{a}_k{e}^{j2\pi kn/N}$$其中，
$$a_k=\sum _{-\infty }^{\infty }{F}_{k+mN}^{\prime },k\in 0,1,...,N-1$$
对上式作如下运算：
$$\sum _{n=0}^{N-1}(x(n)e^{-j2\pi kn/N})=\sum _{n=0}^{N-1}[(\sum _{k=0}^{N-1}{a}_k{e}^{j2\pi kn/N})e^{-j2\pi rn/N}]$$$$=\sum _{n=0}^{N-1}[a_k(\sum _{n=0}^{N-1}{e}^{j2\pi (k-r)n/N})]$$
因为$x(n)$和e^{-j2\pi kn/N}的周期都是N，所以a_k的周期也是N。

离散傅里叶级数变换对

$x(n)<->X(k)$
$$X(k)=\sum _{n-0}^{N-1}(x(n)e^{-j2\pi kn/N})=DFS[x(n)]]$$
$$x(n)=\frac{1}{N}\sum _{k=0}^{N-1}X(k)e^{j2\pi kn/N}=IDFS[X(k)]$$
从上式可以看出，$x(n)X(k)$都以N为周期。其中，$X(k)$表示K倍谐波，也就是2\pik/N的频率分量的值/$X(k)$的周期性表示可以将$x(n)$在任意连续N个谐波上展开。然而$X(k)$的周期性不意味着对应的连续时间信号所有的谐波信号同时存在，就理解成（非官方）离散周期信号的频谱的“模糊”性。

离散傅里叶级数的性质

周期性、线性（显然的）
时域序列移位：$x(n)<->X(k)$则
$$x(n+m)<->W_N^{-km}X(k)$$
特别地$DFS[x(n+lN)]=X(k)$
频域序列移位：若$x(n)<->X(k)$则：
$$W_N^{qn}<->X(k+q)$$
时域周期卷积（难点)：若
$$x_3(n)=x_1(n)\otimes x_2(n)=\sum _{m=0}^{N-1}{x}_1(m)x_2(n-m)$$则
$$X_3(k)=X_1(k)\cdot X_2(k)$$
周期卷积与离散时间序列卷积和的比较：
(周期序列卷积和如下)
$$x_3(n)=x_1(n)\cdot x_2(n)=\sum _{m=-\infty }^{\infty }{x}_1(m)\cdot x_2(n-m)$$
相同点：都需要换元、序列倒置、移位、序列相乘、相加
不同点：卷积和中两序列非周期；周期卷积中两序列为周期。卷积和的求和限是无穷，周期卷积在一个周期内。

频域周期卷积：
若$x_1(n)<->X_1(k),x_2(n)<->X_2(k)$且$x_3(n)=x_1(n)x_2(n)$则
$$X_3(k)=\frac{1}{N}{X}_1(k)\otimes X_2(k)=\frac{1}{N}{X}_1(l)\cdot X_2(k-l)$$
此外，还有对称性等性质。

离散时间傅里叶变换（DTFT）

有两种导出方法，如下：
从连续时间傅里叶变换导出：


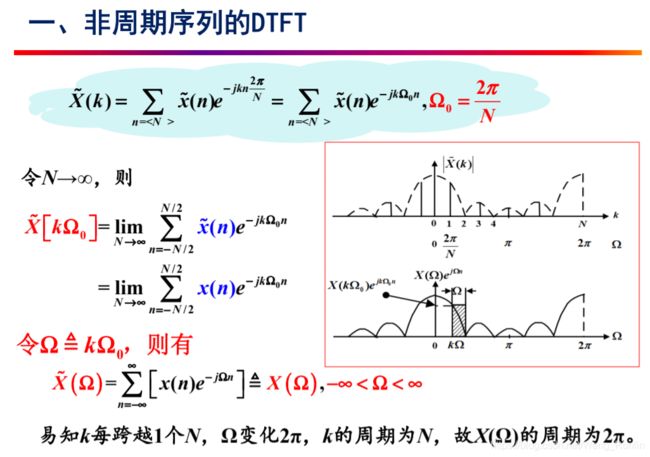
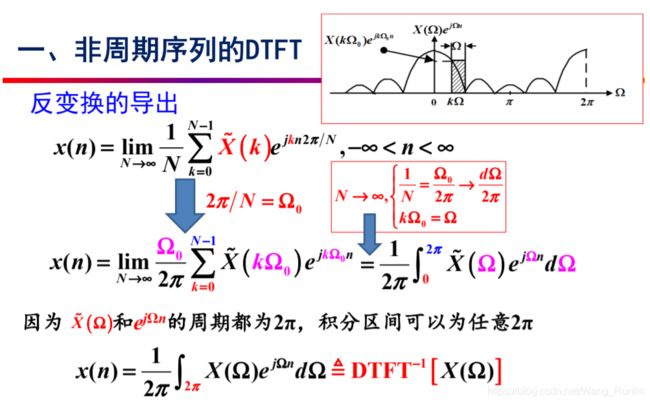
从Z变换导出：（本来应该是由Z变换导出DTFT，一些课本把如下的过程倒过来推导，Z变换由拉普拉斯变换导出；这样好理解但是不符合实际存在的因果关系）

最终得到是：
DTFT变换对：$x(n)<->X(\Omega )$

DTFT正变换：$X(\Omega )={\sum }_{n-=-\infty }^{\infty }x(n)e^{-j\Omega n}$

DTFT反变换(IDTFT)：$x(n)=\frac{1}{2\pi }{\int }_{2\pi }X(\Omega )e^{j\Omega n}d\Omega$
理解（非官方）：
x(n)：无穷多个负指数序列的线性组合，
X(Ω):x(n)中各个频率分量的相对大小。
X(Ω)是连续的，并且以2pi为周期。

DTFT存在的条件是绝对可和。${\sum }_{-\infty }^{\infty }|x(n)|<\infty$。在连续时间傅里叶变换中，w的单位是弧度每秒；而在离散时间傅里叶变换中，Ω单位是弧度。（数字角频率Ω是模拟角频率ω关于抽样频率的归一化值。）
例如，对于矩形脉冲x(n)，（当|n|1时该值取1，否则取0）那么它的离散傅里叶变换
$$X(\Omega )=\sum _{n=-N_1}^{N_1}{e}^{-jn\Omega }=\frac{sin\frac{(2N_1+1)\Omega }{2}}{sin\frac{\Omega }{2}}$$

上方并没有说这是怎么具体来的，这里展开写一下：
算的时候显然不先用欧拉公式转化，转化完是一些凌乱的角度，没法用等比公式，那样就不好了。但还是可以先看看转化后有什么有用的结果：
$$\sum _{n=-N_1}^{N_1}{e}^{-jn\Omega }=\sum _{n=-N_1}^{N_1}(cosn\Omega +isinn\Omega )$$显然，虚部是奇函数，加和后结果是0。那么后续计算出的结果就可以直接不用算虚部了。这里在原形式的等比数列性质展开，再利用上面的结论忽略虚部。
$$\sum _{n=-N_1}^{N_1}{e}^{-jn\Omega }=\frac{e^{j{N}_1\Omega }(1-e^{-j(2N_1+1)\Omega })}{1-e^{-j\Omega }}$$$$=\frac{e^{j{N}_1\Omega }-e^{-j(N_1+1)\Omega }}{1-e^{-j\Omega }}$$$$=\frac{cos{N}_1\Omega }{1-cos\Omega +isin\Omega }$$这里比较迷惑，如果这时候忽略下面的虚部直接算进去，那就错了，因为分母的虚部只是一个中间结果，约去分母的过程中它对最终结果的实数产生了影响，所以不能就这样去掉了，还要再化简。（有点长，就不打字了）

离散傅里叶变换的性质

仍然显然有周期性和线性。
时移性质：$x(n-n_0)<->X(\Omega )e^{-j{n}_0\Omega }$
频移性质：$e^{j{\Omega }_{0}n}x(n)<->X(\Omega -{\Omega }_0)$
对称性：$X(\Omega )=X\ast (-\Omega )$
差分性质(类比微分性质)：$x(n)-x(n-1)<->(1-e^{-j\Omega }X(\Omega )$
求和性质(类比积分性质)：

时域卷积、频域卷积、频域微分与连续时间FT类似。
$$nx(n)<->j\frac{dX(\Omega )}{d\Omega }$$
时域展缩性质（多采样率信号处理）
$$x_{(k)}(n)<->X(k\Omega )$$要求mod(n,k)=0
下面是关于矩形序列内插/抽取时的频谱特性。它的意思就是，在离散序列中按照规则内插（内插的是0）后的频谱特性与比原来更“大条”一点，而抽取时则失去了原来的频谱特性。

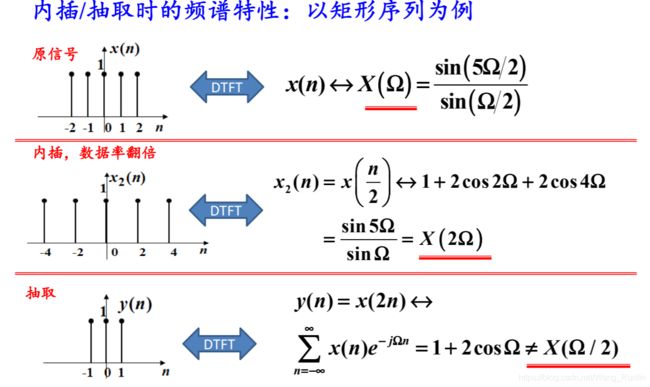
离散信号的帕萨瓦尔定理表述如下：
$$\sum _{n=-\infty }^{\infty }|x(n){|}^2=\frac{1}{2\pi }{\int }_{2\pi }|X(\Omega ){|}^{2}d\Omega$$
同理，序列一个周期的能量等于傅里叶系数在一个周期内的能量。

平稳随机序列功率谱的Z变换表示

$$G_X(z)=\sum _{m=-\infty }^{+\infty }{R}_X(m)z^{-m}$$
由于自相关函数是偶函数（这在联合平稳概率密度部分已经证过），所以$$G_X(z)=G_X(z^{-1})$$
z的收敛域是包含包含单位圆的环形区域，即收敛域为
$$a<|z|<\frac{1}{z},0<a<1$$
由于Z变换是离散傅里叶变换的推广，所以显然有$$G_X(\omega )=G_X(z){|}_{z=e^{j\omega }}$$
自相关函数也可反变换表示为
$$R_X(m)=\frac{1}{2\pi j}{\oint }_C{G}_X(z)z^{m-1}dz$$

例

设随机序列X(n)为X(n)=W(n)+W(n-1)，其中W(n)是高斯随机序列，均值为0，自相关函数
$$R_X(m)={\sigma }^2\delta (m)$$求X(n)的自相关函数和功率谱。
在这里，功率谱既可以用Z变换表示，也可以用离散傅里叶变换表示。X(n)的均值显然为0，而自相关函数按照公式
$$R_X(m)=E[X(n+m)X(n)]$$$$=E\{[W(n+m)+W(n+m-1)][W(n)+W(n-1)]\}$$上式实际上展成了四项，其中两项差距是m，另外两项差距是m-1和m-1。那就有了
$$={\sigma }^2[2\delta (m)+\delta (m+1)+\delta (m-1)]$$
那么功率谱就有了。（一般先用Z变换比较方便，另一种形式将z代换成$e^{j\omega }$即可直接得到）
$$G_X(z)=\sum _{-\infty }^{\infty }{R}_X(m)z^{-m}={\sigma }^2(2+z+z^{-1})$$

应用随机过程分析音乐（语音）信号

概述

随机过程可应用于各个领域，如：通信、生物医学、各种（行业、气象等）指数预测、经济管理决策、以及智能工程等。这里选择音频（语音、音乐等）信号(20~20000Hz)应用简单的随机过程进行分析。

虽然语音信号习以为常，无时不用，听觉也是仅次于视觉的沟通信息的手段，但是语音的信号结构是地球的造化决定的、不是人创造的，只是人发明了英语、汉语、日语等等语言，并且规定了怎么发声而已。至于每种语言的读音为什么就这么规定了，人类自己也说不清。人说不清的东西，而且它还是根据不同情境灵活变化的，而且还是以时间为载体的，那就可以认为语音信号是随机信号，可以用随机过程的方法分析。

语音（歌声）发音特性

这里先考虑人声（说话声或歌声）。在相当长一段时间，人们只知道声音与声音之间有区别，却不知道是何种区别。傅里叶（就还是那个人）发现各个声音之间的区别在于和弦的不同。一个声音的基音和倍音共同组成这个声音的和弦。每个复合音都有一连串的倍音，但并非每个倍音都同样那么明显。

声带产生的声音周期较短、阻尼高，其中包含的频率很多。基因和倍音的频率，取决于肺部用力多少和声带紧张度如何。这些复合音通过口腔共鸣，舌头、上腭、嘴唇的变化都可以影响口腔对声音的阻尼大小，加强或抑制某些频率。把声道看作发音腔体，激励它的频率达到固有频率，则声道会以最大振幅振荡。把这个频率叫共振频率，简称共振峰。至于歌声，只是人脑控制它固定（或平滑过渡）在某个乐音频率罢了。所谓唱歌跑不跑调，就是声带的共振峰是不是在应有的乐音频率上。

包含口腔在内的声道是一个分布参数系统，它有许多自然谐振频率（在这些频率上其转移函数具有最大值）。所以口腔是谐振腔。通常，无论哪国语言，不同的元音是由于口腔共鸣的不同形状造成的。一个元音的第一共振峰频率越低，它的舌位就越高。第二共振峰频率越低，舌位就越靠后。 思考啊 窝 呃 噫 坞 迂的发音。啊的发音，舌头永远在下面，说明它的第一共振峰最高，850Hz左右。（这可能与常识相悖。噫和迂听起来声音高，实际上它们高在第二共振峰。而它的第一共振峰只有300Hz，所以发这两个音的时候舌头要贴着上腭）；而噫和迂发音时，舌头一定是靠后的（而啊音舌头伸出来也没事，这是医院看扁桃体时让喊啊的原因之一），如果舌头靠前，发出的只会是耶。

不论哪国语言，辅音一般能量小、短促（俄语、意大利语、西班牙语等某些弹舌音和美声唱法中的弹舌除外）。辅音的分析比较复杂。它具有类白噪声激励的性质。分析辅音，通常用以下几种样式：直切线样式、间断区样式、噪声样式。

为分析以上汉语发音的基本规则，通常使用离散信号能量/功率谱分析：（因为计算机处理的都是离散的）
$$P_z(n,\omega )=\frac{1}{2N+1}|X(n,\omega )|$$
在时间轴上可视化的功率谱叫语谱图，表示在某个时刻信号能量的分布的情况。对于音乐信号，也可以用这种方法作频谱分析，甚至可以模拟音乐制作软件中的识别旋律的情况。

引子：用python可视化音乐信号的一些统计量

对于连续时间信号，进行功率谱分析之前，往往需要先熟悉频谱分析。频谱相当于能量谱，功率谱相当于是对能量谱做时间平均后得到的结果。这里，用python语言简单可视化一下某首音乐的频谱随时间的分布、同时提取基频（当然，能弄出来只是因为python提供的库中有不少现成的东西）：

首先、导入并试听音乐：

import librosa
import sklearn
audio_path = 'D:\jupyter_deepLearning\i_miss_you.wav'

x,sr = librosa.load(audio_path, sr=44100)

import IPython.display as ipd
ipd.Audio(audio_path)

观察信号的时域波形、频域响度特性（相当于频谱，而不是功率谱。功率谱是自相关后的离散傅里叶变换，而频谱是直接对信号采样后的傅里叶变换）。（响度单位换算为dB，以后听觉特性中详细描述)在这里采用librosa中的短时傅里叶变换函数stft。

import matplotlib.pyplot as plt
import librosa.display

plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr)

X = librosa.stft(x)
Xdb = librosa.amplitude_to_db(abs(X))
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
plt.colorbar()

时域波形：
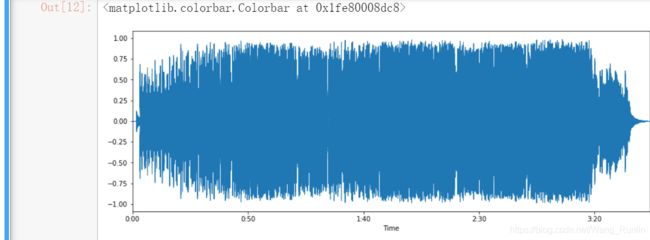频谱：实际上频谱本身又可以看作一个随机过程。在python环境中读取的采样率是44100Hz，根据奈奎斯特定律原则上能读取22050Hz以下的频率，说明该音乐信号在制作时就把频率限制在了10000Hz。可以看到，有一条条红竖线，它们是鼓点所在的时刻（鼓点的能量大，冲激强烈、高次谐波充沛)，以后可以根据这些值探测乐曲速度。而乐音的基音频率多集中在40（贝斯的最低音）~2500Hz，故贴近地表都泛起了红色。

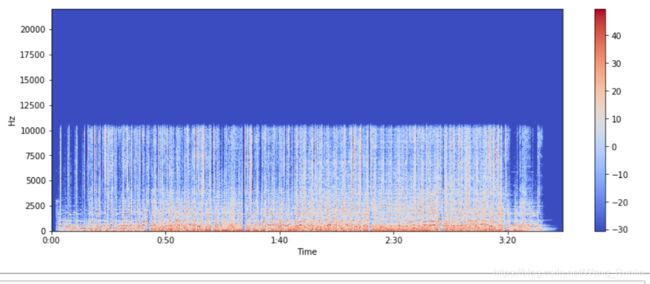
由于乐音频率向上是呈指数增长的，所以使用对数还原到线性可能更直观些。

librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log')
plt.colorbar()

线性（上上图）除了鼓点其他一团糟，而对数图好了许多。已经依稀可见密集的红点，那往往是主旋律的基音频率。

而后，寻找频谱质心：（相当于频谱这个随机过程的均值函数m_x(t)）

#找到这个音乐片段的频谱质心（频谱中心）
spectral_centroids = librosa.feature.spectral_centroid(x, sr=sr)[0]
spectral_centroids.shape
(775,)
# 计算可视化的时间变量（短时傅里叶变换是取窗按帧探测并进行变换的，这里要把帧换回到时间更方便）
frames = range(len(spectral_centroids))
t = librosa.frames_to_time(frames)
# 归一化频谱质心，这样更好看点
def normalize(x, axis=0):
    return sklearn.preprocessing.minmax_scale(x, axis=axis)

librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_centroids), color='r')

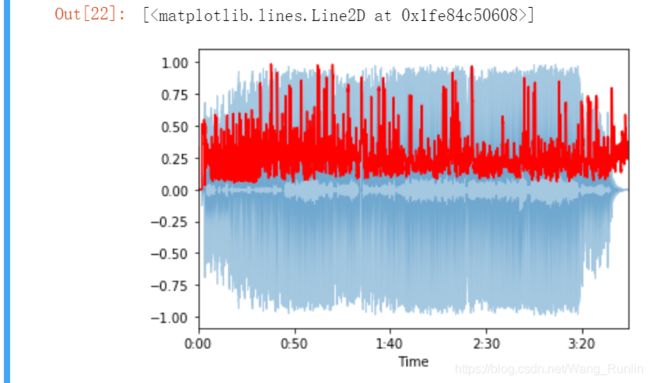
可视化梅尔倒频谱系数（用python可直接实现，以后将尝试用matlab或C一步步实现）

# 梅尔倒频谱系数
x,fs = librosa.load('D:\jupyter_deepLearning\example.wav')
librosa.display.waveplot(x,sr = sr)

mfccs = librosa.feature.mfcc(x,sr = fs)
print (mfccs.shape)
(20,97)
# 画出梅尔倒频谱系数
librosa.display.specshow(mfccs,sr = sr, x_axis = 'time')

最后模拟一下音乐制作软件中音高检测的程序，当然这是用了python中已经写好的模块，直接就干了（没有配合节奏检测，直接分成了512段进行操作。python库中写好的操作原理大概是，把刚才得到频谱中的谐波频率按照2的对数叠起来（就是，比如440Hz是6音，那高八度的6是880，低八度的是220，这样把每个音符的频率成分叠加再放在一起，得到纵坐标表示的pitch class，就是1234567。）

hop_length = 512
chromagram = librosa.feature.chroma_stft(x, sr=sr, hop_length=hop_length)
plt.figure(figsize=(15, 5))
librosa.display.specshow(chromagram, x_axis='time', y_axis='chroma', hop_length=hop_length, cmap='coolwarm')

常用模型

线性时不变系统（LTI）

线性时不变是信号与系统第一章的概念。它既满足叠加原理又具有时不变特性，它可以用单位脉冲响应来表示。

在这里，仍然研究的是歌声或说话声。在线性时不变系统假设中，认为激励源（相当于声带和产生的气流了）和声道(相当于头腔、咽腔的共鸣)是独立的。这为单独讨论声道（相当于转移函数）提供了可能。这种模型在大部分情况下是可以用的，但是当辅元之间的界限不甚明显时，如（扑，特等子，pot等词，或者其他语言中类似的情况）这种方法无效。
这种方法的基本构架是，首先要有脉冲发生器和随机信号发生器，然后这些原信号经过系统（声道，也就是头腔口腔咽腔鼻腔等等）对脉冲进行响应，最后得到生成的语音。

目前还没有生成语音的技术应用于实际（因为它过于复杂且效果甚微），现存的技术叫语音合成（给声音录音、分析语音或音乐信号的成分，然后使用（打散重组、改变音高或音调趋势等手段）合成语音）。

线性时变系统（LTV）
线性时变系统应该考虑转移函数不是固定的，是依照时间变化的。方法是对一段时间求卷积，把有声音调（用声带发声的）部分和脉冲（声道的给出的响应）都看作变量，然后将两者卷积生成最终结果。