LU分解完成利用节点电压法的简易电路求解程序（二）

上一篇博客中我们回顾了LU分解，分析了一个简单的电路并观察到

电导矩阵中的对角线项为节点相连的电导之和，非对角线项等于两个节点之间电导的相反数

与

电流项为独立电流源流入节点与流出节点电流代数和，其中流入节点电路符号为正，流出节点符号为负
我们断言其成立，事实上对于所有仅包含电流源的电阻网络，其总是成立。无论用什么样的分析方法，设出节点电压联立方程，写为矩阵形式后都符合上述规律，由此我们获得由一般电路转化为矩阵形式的关键。其实利用上述规律，我们可以直接写出电路的方程，省去大量分析时间。

3.从电路图到电路的描述

上面我们获得了将电路转化为矩阵方程的方法，而这个过程是我们利用明亮的大眼睛 观察文中给出的图片得到的，而计算机似乎很难办到（图像中的信息提取将在以后的博文中讨论，这大大超出了这篇博文的研究范围），因此我们需要一个能准确描述电路连接方式一段文字（显然最容易想到的是自然语言哦，这个也超出了博文的范围），常用描述电路连接方式的一种语言是SPICE语言，他在各种仿真软件中都可以见到，我们熟知的Pspice就是其一，Pspice利用图形交互界面完成绘制后，会将网络转化为一份SPICE清单，这里面包含了电路的器件，连接，激励源等等。
这里我们仿照SPICE语言完成对电路的简洁描述，为了减低难度，我们对正统的SPICE语言进行大开刀，定义相对简洁的语法。由于电路中的元件只有两个（电阻，电流源），我们简洁用下列方式表示

电阻：R <连接节点A> <连接节点B> <电阻值>
电流：I <连接节点A> <连接节点B> <电流值>

需要注意的是，电流源是一个有向器件，他的电流方向是从节点A到节点B
我们尝试用这种方法对下列电路进行描述

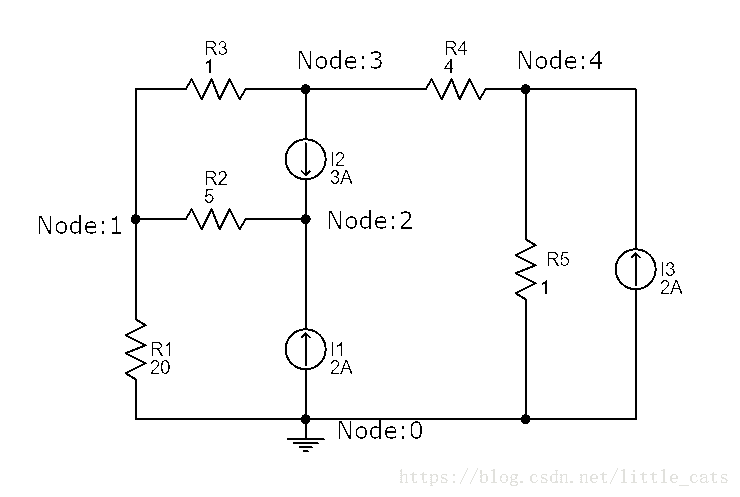
这幅电路还是有点复杂的，它包含了5个电阻3个电流源，图中我们对节点进行了命名，以下是他的描述代码

IDC1 3 2 3
IDC2 0 2 2
IDC3 0 4 2
R1 0 1 20
R2 1 2 5
R3 1 3 1
R4 3 4 4 
R5 4 0 1

这里器件名字只做标识，可有可无。节点为方便起见用数字命名，注意连续。
有了描述代码我们就可以利用它来分析我们的电路。我们可以利用语法分析树的方式来对其进行语法分析，但是写起来还是有点难度的，这里我们使用一个简单粗暴的方式来解析这段描述代码，以下给出代码

    while (!input.eof())
    {
        input >> c;
        switch (c)
        {
        case 'R':
        {
                    while (c != ' '&&!input.eof())
                    {
                        input >> c;
                    }
                    input >> c;
                    while (c != ' '&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;
                    }
                    x = SumUp(i);
                    if (x > SumNode) SumNode = x;
                    i = 0;
                    input >> c;
                    while (c != ' '&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;
                    }
                    y = SumUp(i);
                    if (y > SumNode) SumNode = y;
                    i = 0;
                    input >> c;
                    while (c != '\n'&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;

                    }
                    res = SumUp(i);
                    i = 0;
                    ConMat[x][y] += 1.0/res ;
                    ConMat[y][x] += 1.0 / res;
                    x = 0; y = 0; res = 0;
                    break;
        }
        case 'I':
        {
                    SumIdc++;
                    while (c != ' '&&!input.eof())
                        input >> c;
                    input >> c;
                    while (c != ' '&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;

                    }
                    x = SumUp(i);
                    i = 0;

                    input >> c;
                    while (c != ' '&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;
                    }
                    y = SumUp(i);
                    i = 0;

                    input >> c;
                    while (c != '\n'&&!input.eof())
                    {
                        Var[i] = c;
                        i++;
                        input >> c;

                    }
                    idc = SumUp(i);
                    i = 0;

                    IdcMat[x][y] += idc;
                    x = 0; y = 0; idc = 0;
                    break;
        }
        default:break;
        }
    }
}

这里连用了几个while，虽说冗长不太美观，功能是没问题的。程序逐个字符读取，空格作为分割，换行作为结束，一行三个参数一次读取完全。实际上如果有多个器件我们还是可以利用状态机优化一下的，这里只有两个器件也不弄那么复杂啦。

4.电导与电流的存储

上面代码中我们可以看到把电导和电流分别存放在数组ConMat[][]和IdcMat[][]中，关于电导和电流的存放方式，还是来写一下。
首先来说说电导。由于电阻是个无极性元件，正着接反着解电导不会改变，这种情况下我们其实可以使用“无向图”来表示，最简单的方法就是使用一个二维数组，存储如下：

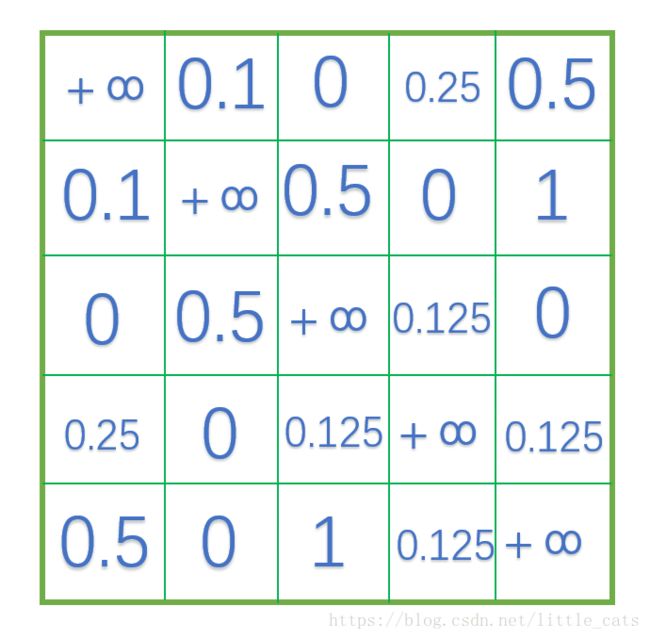
可以看到，这个数组式沿对角线对称的，这个就是无向图的一个特点。我们需要求某一结点所连接的电导，只需要在图中把该节点那一列（或行）数字全部相加即可
例如，求解节点3连接的电导之和，只需要把第4列（或行）相加

0.25+0.125+0.125=0.5 0.25 + 0.125 + 0.125 = 0.5

如果想要求解节点2与节点3之间连接的电导，只需要找到第3行第4列那个格子就可以了，为 0.125 0.125
实际上，这里的无穷大完全可以使用0代替，本身作用不大，由于节点0式参考节点，在方程中不会出现。
按照前文给出的规则，这个电导数组表示的矩阵可以写成

Gij=⎡⎣⎢⎢⎢0.3−0.200−0.21.325−0.125−10−0.1230.5−0.1250−1−0.1251.625⎤⎦⎥⎥⎥ G i j = [ 0.3 − 0.2 0 0 − 0.2 1.325 − 0.123 − 1 0 − 0.125 0.5 − 0.125 0 − 1 − 0.125 1.625 ]

需要注意的是，有几个非参考节点，对应的就有几个方程组。

对于电流，我们使用有向图来存储，有向图与无向图直观的区别就是对角线是否对称。存储的方式同电导一致，这里不再赘述，我们同样可以利用上述规则产生需要的电流向量。
在实际代码中，只需要互换脚标即可产生无向图

//这是无向图，交换脚标
ConMat[x][y] += 1.0 / res ;
ConMat[y][x] += 1.0 / res;

//这是无向图，不需要交换脚标
IdcMat[x][y] += idc;

产生电导矩阵的代码如下

void Get_MatG()
{
    int i, j;
    double sum = 0.00;
    for (i = 0; i <= SumNode; i++)
        for (j = 0; j <= SumNode; j++)
        {   
            sum += ConMat[i + 1][j];
            if (i != j)
            {
                MatG[i][j] = -ConMat[i + 1][j + 1];
                MatG[j][i] = -ConMat[i + 1][j + 1];
            }
        }
        MatG[i][i] = sum;
        sum = 0;
    }

电流向量产生代码如下

void Get_MatI()
{
    double sum_in = 0.0, sum_out = 0.0;
    int i, j;
    for (i = 0; i <= SumNode; i++)
    {
        for (j = 0; j <= SumNode; j++)
        {
            sum_out += IdcMat[i][j];
            sum_in += IdcMat[j][i];
        }

        if (i>0)
            MatI[i-1] = -sum_out + sum_in;
        sum_in = 0;
        sum_out = 0;
    }
}

完成了电导与电流矩阵的生成，我们可以来求解节点电压。

5.节点电压的求解

对于任意一个电路，我们输入了它的描述，就可以得到有关其节点的电导，电流矩阵，从而完成求解。
利用LU分解，首先我们需要对电导矩阵进行LU分解，得到一个上三角矩阵U与下三角矩阵L，代码如下

for (i = 0; i < SumNode - 1; i++)
    {
        for (j = i; j < SumNode - 1; j++)
            MatG[j + 1][i] /= MatG[i][i];
        for (j = i; j < SumNode - 1; j++)
        for (k = i; k < SumNode - 1; k++)
            MatG[j + 1][k + 1] -= MatG[i][k + 1] * MatG[j + 1][i];
    }

接着求解下三角矩阵系统

    Maty[0] = MatI[0] / L[0][0];
    for (i = 1; i < SumNode; i++)
    {
    for (j = 0; j < i; j++)
        sum += L[i][j] * Maty[j];
    Maty[i] = (MatI[i] - sum) / L[i][i];
    sum = 0;
    }

然后是上三角矩阵系统

MatV[SumNode - 1] = Maty[SumNode - 1] / U[SumNode - 1][SumNode - 1];
    for (i = SumNode - 2; i >= 0; i--)
    {
        for (j = SumNode - 1; j >i; j--)
            sum += U[i][j] * MatV[j];
        MatV[i] = (Maty[i] - sum) / U[i][i];
        sum = 0;
    }
    sum = 0;

数组MatV里面存储着就是求解出的各节点电流。
在这里，我们对上面给出的电路描述进行求解：

输入:input.txt
IDC1 3 2 3
IDC2 0 2 2
IDC3 0 4 2
R1 0 1 20
R2 1 2 5
R3 1 3 1
R4 3 4 4 
R5 4 0 1

输出：
NODE:4

24.7826
49.7826
21.0217
2.76087

达到求解节点电压的目的。
通过这个实例，我们对LU分解的正确性进行了验证，并在用于求解一类电路。我们注意到，电导矩阵对角线上的元素总是非零，这使得LU分解无需选择主元。对于对角线上存在0元素时我们更进一步需要使用LUP分解，其中P是一个置换矩阵。

最后，我们可以通过这个实例进行许多拓展，例如包含电压源我们如何处理（利用超节点法求解），对于受控源我们又如何处理。这类问题在直流电路中颇为常见，也涵盖了直流电路大部分内容，同样在直流电路中更高级的求解技巧例如叠加定理同样可以用在其中。