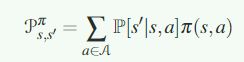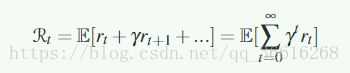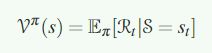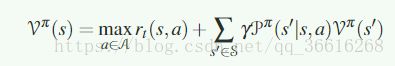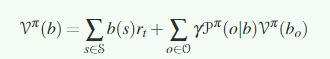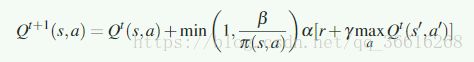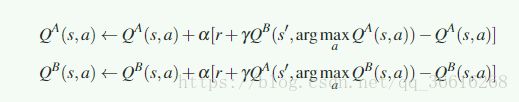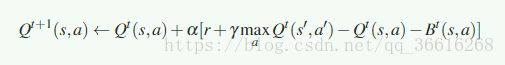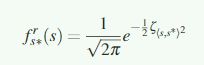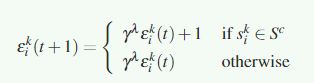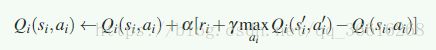Deep Reinforcement Learning Variants ofMulti-Agent Learning Algorithms
这是一个80页的论文,有效内容70页,10页reference。
本篇论文主要介绍了两个算法,这篇论文写自2016年,也就是DQN发表一年后,所以这一年结合深度网络写rl的文章很多。
下面我们就介绍一下本篇论文。我会摘取一些有用没用的大家都知道的以前的知识做铺垫。
这篇文章主要讲述了两种算法,DRUQN(deep repeated update Q-network )和DLCQN(Deep loosely Coupled Q-Network)
首先 DRUQN是为了解决Q-learning中频繁更新某些特定的动作-值对导致的性能下降。
DLCQN尝试将每次状态分解为 独立动作 与 需要与其他Agent协调的动作
本文使用的是乒乓球的环境。首先介绍一下什么是No-stationarity的环境,多个agent不断地改变环境,不像再单agent中,agent只需要观察自己动作的影响,在MARL中,agents需要在相同的环境下相互影响和共同学习的。一个agent不仅要与自己的action管理也要与观察到的其他agent的动作关联,同时其他的agent也要开始调整自己的动作,可能造成过去学到的东西现在不在被保留。因此在No-staionarity的环境下,某个动作的潜在效益可能会过时。
在这里说一下non-stationarity的环境:我的个人理解
比如环境本身是变化的,如reward-function会随着时间的变化而变化。
一般在单agent中都是stationarity的(reward与转移都稳定,不在发生变化),而在多agent中则多为non-stationarity(多agent中其他agent的策略发生改变,或者环境发生改变,都可以理解为造成non-stationarity的原因,可以理解为e-greedy策略造成的,也可以理解为在不采用e-greedy的策略的时候,网络的更新造成的,只要有网络的更新,就会对最后的策略造成影响。又比如在AC中,actor采取动作的时候就是根据一个网络,而没有e-greedy,当他更新这个网络的时候,我们就说从另一个agent的角度,这个agent的策略在发生变化)
Markov Decision Processes
MDP是memoryless和history indepentent的,也就未来的状态只与当前状态有关,而与过去发生的所有状态无关。
当前的状态被假设足够用以预测未来的状态
标注每个状态的reward可以写为:
为了解决MDP过程,引入了一个状态值函数,在策略pai的情况下:
最优的v则表示为:
下面就是早期的根据dp发展出来的策略迭代算法与值迭代算法:
Partially Observable Markov Decision Processes
MDP假设完全可观测,也就是说在当前状态中,可以获取全部的状态信息,用于进行决策。
但是在现实世界中,大部分情况下是不可观测全部信息的,因此就有了POMDP
它是MDP的一个扩展,![]() :
:
此时决策不能但由当前的state决定,需要包含所有历史(包括action,reward,obeservation),
因此构建了一个belief state b(s)
这个belief state将会作为满足MDP属性的充足的信息。此时:
这里很多情况下都需要拟合这个b(s)
Decentralized Markov Decision Processes
Dec-MDP是一个POMDP的扩展,在这个framework中,agent可以协调合作等级。利用这个框架,一个agent可以独立获取信息,也可以协作获取信息更新,这取决于他们之间需要协作的程度
![]() :
:
下面就说到了强化学习了
提到了Q-learning以及Approximating Action value Functions
MARL
一个policy是最优的和固定的,当它是最好的政策并且随着时间,不会发生改变。
在多agent环境中,显然是不固定的。
Repeated Update Q-learning
我在读完这个算法之后,觉得这个算法不是为了解决多agent下的合作问题的,而是单独为了解决Overestimation
导致Overestimation的原因是:
或者可以,单纯的理解每次都是用max,导致最后的估计会变高。
RUQL的灵感来自于policy bias,因为在Q-learning中只有被多次选中的action-value才会更新
也就是可以说这个值的有效率可以近似于这个state选中这个action的概率。类似于UCB的confidence
这也就强化了某些状态的倾向。而在Non-stationarity的环境下,这个问题会更加严重,因为以前的policy在这一次不一定还可以得到benefice
如果一个agent可以在时间并行执行所有的可能操作,那么所有操作对应的信息都可以被同时更新。
因此RUQL就提出了根据选中这一动作的概率来更新值。
早在2010年就有人提出了类似的思路,见算法(Frequency Adjusted Q-learning)
同时2010年 double Q-learning提出:
2012年 Bias Corrected Q-learning 一个修正项 B被引入,
(其他这些之后不久都会补上文章的)
因此RUQL知识解决了non-statinarity环境中的一个问题,还未涉及到多agent
Loosely Coupled Learning
Agent indenpendence
![]() 是一个agent在状态s采取动作的独立性,越大,表示可以独立,而不需要考虑其他的agent
是一个agent在状态s采取动作的独立性,越大,表示可以独立,而不需要考虑其他的agent
Determining Independence Degree ![]()
一个agent在一个给定state下采取动作的独立性根据他所收到的负面结果进行调整。
在每个状态会收到一个负面reward,用一个类高斯扩展函数表示上一个state的作用范围:
![]() 用来衡量state之间的相似性,当state之间相似性高的时候 f 的 值也会变大,这表示状态s的大量参与导致了负面的影响
用来衡量state之间的相似性,当state之间相似性高的时候 f 的 值也会变大,这表示状态s的大量参与导致了负面的影响
重要的是需要辨别哪个state状态是属于导致negative reward的状态轨迹。
通过资格追踪,信用可以被分给不同的受negative reward影响的州:
![]() 是折扣因子,
是折扣因子,![]() 是 delay参数,
是 delay参数,![]() 是状态轨迹(表示与负面奖励有关的一系列state)
是状态轨迹(表示与负面奖励有关的一系列state)
然后,将扩散函数的结果和资格跟踪结果组合起来,得到一个ψ基值,表示合作的必要性。
ψ与独立度成反比,因此(归一化函数)
独立度调整算法:
下面是Coordinated Learning:
当需要协作学习的时候就用到了Dec-MDP了,如果只有两个agent,那么![]()
![]()
对于agent i 的写作算法:
js表示joint state,联合学习需要用下买你的更新公式:
单个agent学习,用:
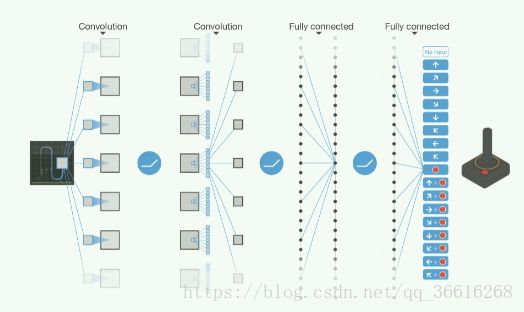
下面就是添加了Deep Network的这两种算法了
Deep Repeated Update Q-Learning
Deep Loosely Coupled Q-Learning:
最后还做了三个实验对三种情况进行比较,其中DRUQN的效果总体上最好,DLCQN需要进一步研究(最好是能拟合独立度)
说说第二个实验和第三个实验,第二个实验室分别用各种方法打乒乓球,保持球不掉落,这里DRUQN是最好的,而DLCQN最差
第三个实验室,是分别VS,其中DRUQN和DLCQN都比DQN的效果要好