RSA算法原理及Rsa-Tools
The RSA encryption algorithm is an asymmetric encryption algorithm. RSA is widely used in public key cryptography and electronic commerce. RSA was proposed in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman. All three of them were working at the Massachusetts Institute of Technology. RSA is composed of the first three letters of their last names.
文章目录
- RSA算法原理
- 什么是RSA
- RSA加密
- 公钥=(E,N)
- RSA解密
- 私钥=(D,N)
- 生成密钥对
- 1. 求N
- N=p∗q
- 2. 求L
- L=lcm(p-1,q-1)
- 3. 求E
- 1 < E < L
- gcd(E,L)=1
- 4. 求D
- 1 < D < L
- (E*D)mod L = 1
- 实践下吧
- 求N
- 求L
- 求E
- 求D
- 加密
- 解密
- Rsa-Tools
- 怎样使用
RSA算法原理
什么是RSA
RSA算法是现今使用最广泛的公钥密码算法,也是号称地球上最安全的加密算法。在了解RSA算法之前,先熟悉下几个术语。
根据密钥的使用方法,可以将密码分为对称加密和公钥加密
**对称密码:**加密和解密使用同一种密钥的方式
**公钥密码:**加密和解密使用不同的密码的方式,因此公钥密码通常也称为非对称密码。
RSA加密
RSA的加密过程可以使用一个通式来表达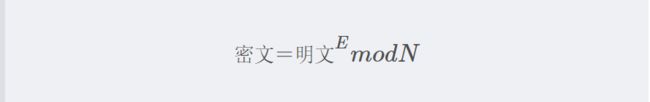
也就是说RSA加密是对明文的E次方除以N后求余数的过程。
从通式可知,只要知道 E 和 N 任何人都可以进行RSA加密了,所以说E、N是RSA加密的密钥,也就是说E和N的组合就是公钥,我们用(E,N)来表示公钥。
公钥=(E,N)
不过E和N不并不是随便什么数都可以的,它们都是经过严格的数学计算得出的,关于E和N拥有什么样的要求及其特性后面会讲到。顺便啰嗦一句E是加密(Encryption)的首字母,N是数字(Number)的首字母
RSA解密
RSA的解密同样可以使用一个通式来表达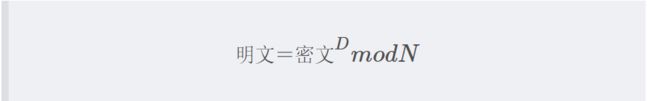
也就是说对密文进行D次方后除以N的余数就是明文,这就是RSA解密过程。知道D和N就能进行解密密文了,所以D和N的组合就是私钥
私钥=(D,N)
从上述可以看出RSA的加密方式和解密方式是相同的,加密是求“E次方的mod N”;解密是求“D次方的mod N”
此处D是解密(Decryption)的首字母;N是数字(Number)的首字母。
小结下
| 公钥 | (E,N) |
| 私钥 | (D,N) |
| 密钥对 | (E,D,N) |
| 加密 | 密文=明文^E mod N |
| 解密 | 明文=密文^D mod N |
生成密钥对
既然公钥是(E,N),私钥是(D,N)所以密钥对即为(E,D,N)但密钥对是怎样生成的?步骤如下:
- 求N
- 求L(L为中间过程的中间数)
- 求E
- 求D
1. 求N
准备两个质数p,q。这两个数不能太小,太小则会容易破解,将p乘以q就是N
N=p∗q
2. 求L
L 是 p-1 和 q-1的最小公倍数,可用如下表达式表示
L=lcm(p-1,q-1)
3. 求E
E必须满足两个条件:E是一个比1大比L小的数,E和L的最大公约数为1(互质)
用gcd(X,Y)来表示X,Y的最大公约数则E条件如下:
1 < E < L
gcd(E,L)=1
之所以需要E和L的最大公约数为1是为了保证一定存在解密时需要使用的数D。现在我们已经求出了E和N也就是说我们已经生成了密钥对中的公钥了。
4. 求D
数D是由数E计算出来的。D要小于L且D、E之间必须满足以下关系:
1 < D < L
(E*D)mod L = 1
只要D满足上述2个条件,则通过E和N进行加密的密文就可以用D和N进行解密。
简单地说条件2是为了保证密文解密后的数据就是明文。
现在私钥自然也已经生成了,密钥对也就自然生成了。
小结下:
| 求N | N= p * q ;p,q为大质数 |
|---|---|
| 求L | L=lcm(p-1,q-1) ;L为p-1、q-1的最小公倍数 |
| 求E | 1 < E < L,gcd(E,L)=1;E,L最大公约数为1(E和L互质) |
| 求D | 1 < D < L,(E*D) mod L = 1 |
实践下吧
我们用具体的数字来实践下RSA的密钥对对生成,及其加密解密对全过程。为方便我们使用较小数字来模拟。
求N
我们准备两个很小对质数,
p = 17
q = 19
则N = p * q = 323
求L
L = lcm(p-1, q-1)= lcm(16,18) = 144
144为16和18对最小公倍数,也就是中间值L
求E
求E必须要满足2个条件:1 < E < L ,gcd(E,L)=1
即1 < E < 144,gcd(E,144) = 1
E和144互为质数,5显然满足上述2个条件
故E = 5
此时公钥=(E,N)= (5,323)
求D
求D也必须满足2个条件:1 < D < L,(E*D) mod L = 1
即1 < D < 144,(5 * D) mod 144 = 1
显然当D= 29 时满足上述两个条件
1 < 29 < 144
5*29 mod 144 = 145 mod 144 = 1
此时私钥=(D,N)=(29,323)
加密
准备的明文必须时小于N的数,因为加密或者解密都要mod N其结果必须小于N
假设明文 = 123
则 密文=明文^E mod N=123^5 mod 323=225
解密
明文=密文^D mod N=225^29 mod 323=123
解密后的明文为123。
参数N和E是公开的但是D是私有的并且绝不能公开!P和Q在生成密钥后便不再需要了,但是必须销毁。
为了从公钥(N,E)得到D,需要试图分解N为它的两个素数因子。对于一个很大的模数N(512位或更大)
要想分解出它的P和Q是件非常困难的事。RSA 加密模式的所有安全性都依赖于大数分解(但是还没有数学上的证明)。
参考:https://blog.csdn.net/dbs1215/article/details/48953589
Rsa-Tools
RSA是第一个安全,实用的公钥加密算法,已成为国家标准,是目前应用广泛的公钥加密体制,RSA的基础是数论的欧拉定理,它的安全性依赖于大整数因子分解的困难性。
RSA-Tool是一款RSA算法辅助工具,非常方便大家写rsa算法。

简单使用方法
RSA-Tool 2 特点:
- 安全生成密钥对
- 密钥测试对话框
- 支持复合进制
- 自动进行选择的数制转换
- 支持到4096字节
参数
P= 第一个大素数
Q= 第二个大素数 (P和Q的长度不能相差太大!)
E= 公钥 (一个随机数,必须满足:GCD(E,(P-1)(Q-1))==1) (注:即E和(p-1)(Q-1)互素)
N= 公用模数,由P和Q生成:N=PQ
D= 私钥 :D=E^(-1) mod ((P-1)*(Q-1))
怎样使用
为了生成符合要求的随机RSA密钥,请类似如下操作:
1、在“Number Base”组合框中选择进制为 10 ;
2、单击“Start”按钮,然后随意移动鼠标直到提示信息框出现,以获取一个随机数种子;
3、在“KeySize(Bits)”编辑框中输入 32 ;(秘钥长度)
4、单击“Generate”按钮生成公钥e;
5、复制“Prime§”编辑框中的内容到“Public Exp.(E)”编辑框;
6、在“Number Base”组合框中选择进制为 16 ;
7、记录下“Prime§”编辑框中的十六进制文本内容(公钥e)。
8、再次重复第 2 步;
9、在“KeySize(Bits)”编辑框中输入您所希望的密钥位数,从32到4096,位数越多安全性也高,但运算速度越慢,一般选择1024位足够了;
10、单击“Generate”按钮生成私钥d;
11、单击“Test”按钮测试,在弹出的“Message to encrypt”编辑框中随意输入一段文本,然后单击“Encrypt”按钮加密,再单击“Decrypt”按钮解密,看解密后的结果是否和所输入的一致,如果一致表示所生成的RSA密钥可用,否则需要重新生成;
12、到此生成完成,“Private Exp.(D)”编辑框中的内容为私钥(d),第7步所记录的内容为公钥(e),“Modulus (N)”编辑框中的内容为公共模数(n),请将上述三段十六进制文本保存起来即可。
(先生成E才能再生成D)
重点注意:此公钥( E )的进制默认是hex,解题时一定要注意,先把题目给出的E换为十六进制,而且要先把number base(整体所有的进制) 改为10,然后再注意公钥( E )处要填十六进制。
例题:
下载一个txt,里面写着:
在一次RSA密钥对生成中,假设p=473398607161,q=4511491,e=17
求解出d作为flag提交
得出结果278573880289078487不对,原因在于没有换好公钥进制,此工具默认是hex不是十进制,先把17换为十六进制:11(Public Exponent(E)处只能填十六进制的,上面标了)
错图:
![]()
正确图:
![]()
然后点击那个Calc.D就算出d了。