opencv轮廓检测之椭圆检测-----算法篇(10)--FindContours函数算法解释

Topological structural analysis of digitized binary images by border following 1985  

出于对版权的考虑,  这里只附上论文名,  墙内百度文库可以找到.  资源共享是好事, 但请大家尊重版权不要拿不是自己的东西来赚积分

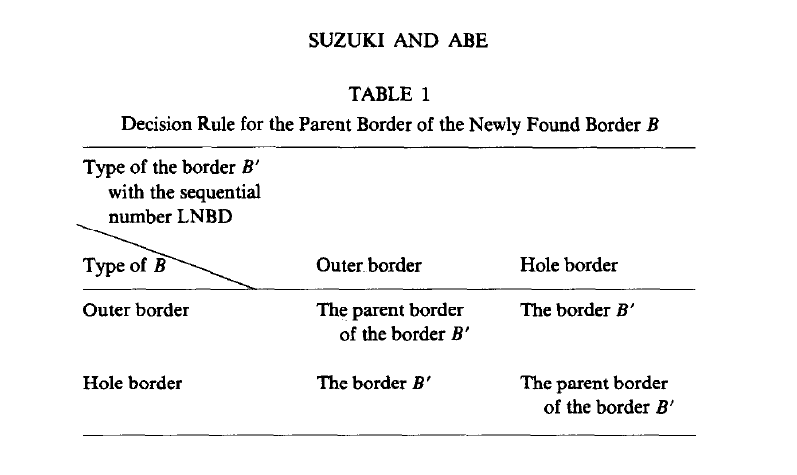
首先介绍了基本概念

       1. 上下左右极限位置构成了frame, 假定frame像素由0 构成

       2. 由像素0构成的componet 如果包含边框, 那将其称之为background, 反之不包含,  则称之为hole

       3. 定义一:  一个像素1的neighborhood 中有一个像素为0, 那么称这个像素为 border point(算了不往下翻译了,  )

                       In the 4- (8-) connected case, a 1-pixel (i, j) having a 0-pixel ( p, q) in its 8- (4) neighborhood 

                                                                                                                                  is calleda border point.

                         It is also described as “a border pointbetween a 1-component S1, and a 0-components S2,”

                       if (i, j) is a member of S1 and (p, q) is a member of S2.

           定义二: (surroundness among connected components).

                        For given two connected components S1 and S2 in a binary picture, 

                     if there exists a pixel belonging  to S2 for any 4-path from a pixel in S1 to a pixel on the frame, 

                     we say that S2 surrounds S1. 

                         If S2 surrounds S1 and there exists a border point between them, then
                     S2 is said to surround S1 directly.

           定义三: (outer border and hole border). 

                        An outer border is defined as the set of the border points between an arbitrary 1-component 

                     and the 0-component which surrounds it directly. Similarly, we refer to the set of the border points

                     between a hole and the 1-component which surrounds it directly asa hole border.
                        We use the term “border” for either an outer border or a hole border. Note that the
                     hole border is defined as a set of 1-pixels (not 0-pixels)as well as the outer border.

           定义四:

                       The parent border of an outer border between a
                     1-component S1 and the 0-component S2 which surrounds S1 directly is defined as:
                 (1) the hole border between S2 and the 1-component which surrounds S2directly, if S2 is ahole;
                 (2) the frame of the picture, if S2 is the background.

           定义五:

                          For two given borders B0 and Bn of a binary picture, we say that Bn surrounds B0 is there exists a                         sequence of border B0, B1, . . . , Bn such that Bk if the parent border of Bk-1, for all k (1 <= k <= n)

             对应下面的图看看就明白它说什么了

       

然后给出了两个算法

       一个是确定这些border的包含关系

       一个是只找最外层的border

算法1:                         https://en.wikipedia.org/wiki/Raster_scan

                                   https://en.wikipedia.org/wiki/Raster_graphics  (TV raster 什么鬼..)

              

          当某像素(i,j)同时满足(a)(b)两个条件时,(i, j) must be regarded as the starting point of theouter border.

                   然后给它编号(编号唯一,由NBD指定)

          

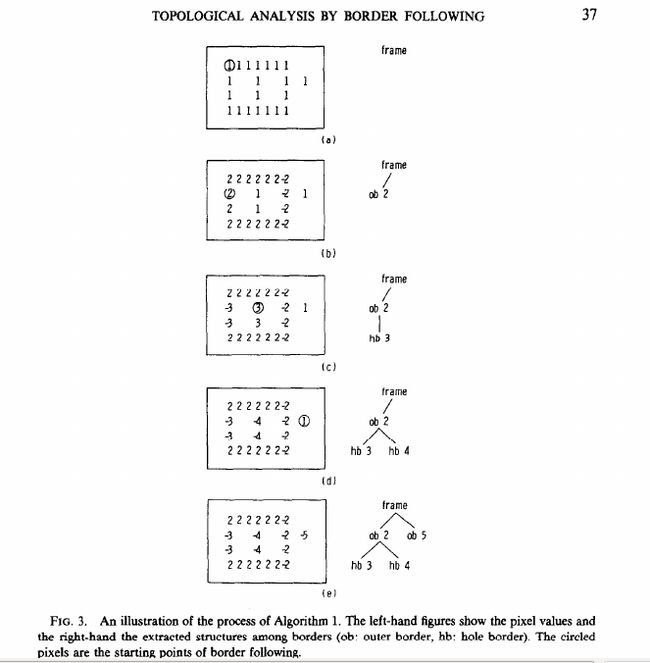
                               由上表鉴定父子关系(parent)

                   从starting point 开始,  把boders都编上号,  确定关系,  应该就这些内容了

                    

                  黑压压的字看着都头疼,  看看图就很清楚了,   如图所说,   这个算法的整个过程

                          然后接下来一堆解释,   对照着图看看就好

算法2(略)

void findContours( InputOutputArray image, OutputArrayOfArrays contours, OutputArray hierarchy, 

int mode, int method, Point offset=Point() )

mode     关于这几种mode请看下面的图

– Contour retrieval mode (if you use Python see also a note below).

– CV_RETR_EXTERNAL retrieves only the extreme outer contours. 
It sets hierarchy[i][2]=hierarchy[i][3]=-1 for all the contours.
– CV_RETR_LIST retrieves all of the contours without establishing any hierarchical relationships.
– CV_RETR_CCOMP retrieves all of the contours and organizes them into a two-level
hierarchy. At the top level, there are external boundaries of the components. At the
second level, there are boundaries of the holes. If there is another contour inside a hole of
a connected component, it is still put at the top level.
– CV_RETR_TREE retrieves all of the contours and reconstructs a full hierarchy of nested
contours. This full hierarchy is built and shown in the OpenCV contours.c demo.

图片来源: learning opencv

method    原文[TehChin89]

– CV_CHAIN_APPROX_NONE stores absolutely all the contour points. That is, any 2
subsequent points (x1,y1) and (x2,y2) of the contour will be either horizontal, vertical
or diagonal neighbors, that is, max(abs(x1-x2),abs(y2-y1))==1 .
– CV_CHAIN_APPROX_SIMPLE compresses horizontal, vertical, and diagonal seg-
ments and leaves only their end points. For example, an up-right rectangular contour
is encoded with 4 points.
– CV_CHAIN_APPROX_TC89_L1,CV_CHAIN_APPROX_TC89_KCOS applies one
of the flavors of the Teh-Chin chain approximation algorithm. See [TehChin89] for de-
tails

图片来源: [TehChin89]

关于用findContours中method– CV_CHAIN_APPROX_SIMPLE

输入图像 :   

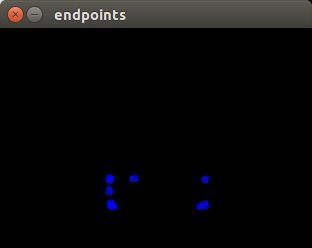
    std::vector<std::vector<cv::Point>> endpoints;

    cv::Mat endpoint(srcEmpty.size(),CV_8UC3,cv::Scalar(0,0,0));

    cv::findContours(srcEmpty,endpoints,CV_RETR_LIST,CV_CHAIN_APPROX_SIMPLE);

    for(int i =0; i< endpoints.size();++i){

        for(int j  = 0; j< endpoints[i].size();++j)

            cv::circle(endpoint,endpoints[i][j],3,cv::Scalar(255,0,0));

    }

    cv::imshow("endpoints", endpoint);

对每个end points 画圆

输出图像:              

比如本人尝试提取车牌的最外层轮廓

    std::vector<cv::Vec4i> hierarchy;

    cv::Mat imgEmpty(img.size(),CV_8UC1,cv::Scalar(0));

    cv::findContours(img,outerline,hierarchy,CV_RETR_EXTERNAL,CV_CHAIN_APPROX_NONE);

    cv::drawContours(imgEmpty, outerline,-1, cv::Scalar(255),1,cv::LINE_8,hierarchy,1);

    cv::imshow("outerline",imgEmpty);

原图是这样

结果是

关于对车牌区域的处理, 为寻找车牌边缘轮廓

我分别用了Sobel, Canny, Laplacian of Gaussian-filtered , Sobel与Laplacian后面接着用了二值化

看起来效果最好的是Canny,  而Sobel外围轮廓太弱没有办法找到,

Laplacian成了这个模样, 虽说可以改变参数, 但是Sobel 与 Laplacian很难找到能够通用的参数吧

即便是看起来最好的Canny, 下一步我想进行的霍夫变换检测直线也没有办法顺利进行

难道只能进行形态学变换?然后对该联通区域进行填充?