数据结构PTA选择填空错题

 

在循环队列中，队头指针与队尾指针是可以改变的，举例此题，长度为6的队列下标为0~5，front=rear=0，插入5个元素，rear=5,删除5个元素，front=5，（目的是让front大）再插入1个元素，rear=0,  front>rear

"最快的排序算法"  时间复杂度远不到N^2  (至少可以达到n logn)

尾指针指向最后一个元素，（节点之间并没有指向其直接前驱的指针），修改尾指针，再free掉最后一个节点可以删除一个节点，但是还要修改倒数第二个节点的next指向空，否则它指向一个已经释放的内存，所以还需重头开始找到倒数第二个节点。

此题与严蔚敏版数据结构中的定义不同，按书上来应为S->top==0  或者S->top==S->base，（S使用了-> 代表这里S是一个指针，S->top代表栈中成员top,是一个地址，而*（S->top）才是top所指的元素）

队尾元素位置不同于队尾下标，队尾下标是队尾元素位置的下一个位置。

由三对角矩阵性质得，除了第一行与最后一行非0 数为2，其余每行非0数为3，m30 30 是第（2+28*3+2）个数，注意30,30在主对角线上，则他的前一个非0，他自己非0，所以是加2，下标从0开始，所以他对应下标为（2+28*3+2-1）=87

逆波兰式求表达式的值

       一棵树的节点数减边数等于一，N-K=树的个数

       没有右子树，根节点是中序遍历的最后一个节点，是前序遍历的第一个节点

假设存在这样一棵树，二度节点为x,叶子节点数为x+1,一度节点数为2016-（2x+1），  2016-（2x+1）=16  解x非整数所以错误

无向图对称矩阵，存储下三角矩阵

有向图中无环时，也可以用DFS进行拓扑排序，最先退出DFS的顶点即出度为0的点是拓扑排序中最后一个顶点，所以也可以检查图中有无回路

16条边对应32个节点，除去已知节点，还剩8个度，每个节点最多为二度节点 所以节点最少为4 +3+4=11

拓扑排序中，使用栈或队列的目的是省去每次遍历寻找度数为0的节点，初始化栈之后首先把所有度=0的节点入栈，之后寻找节点u并入结果集合之后再次更新（所有以u为弧头的边所关联的另一节点v的入度减一），在此处判断，入度减为0，进栈，下一次操作是栈顶进行（新入栈的节点）而队列在进行下次操作队头出来的是之前的节点，可能并不是刚刚更新入栈的节点，造成序列不一样

图的最小生成树与最短路径没有太大的关联，只不过在一定程度上应用了贪心算法的思想而已，但二者区别却比较明显。

区别：

     最小生成树能够保证首先是树（对于n个顶点的图只有n-1条边），其次保证任意两个顶点之间都可达，再次保证这棵树的边权值之和为最小，但不能保证任意两点之间是最短路径；

     最短路径保证从源点S到目地点D的路径最小（有向图中不要求终点能到起点），不保证任意两个顶点都可达;

    最小生成树是用最小代价遍历整个图中所有顶点，所有的权值和最小。而最短路径只是保证出发点到终点的路径和最小，不一定要经过所有顶点；最小生成树是到一群点（所有点）的路径代价和最小，是一个n-1条边的树，最短路径是从一个点到另一个点的最短路径；

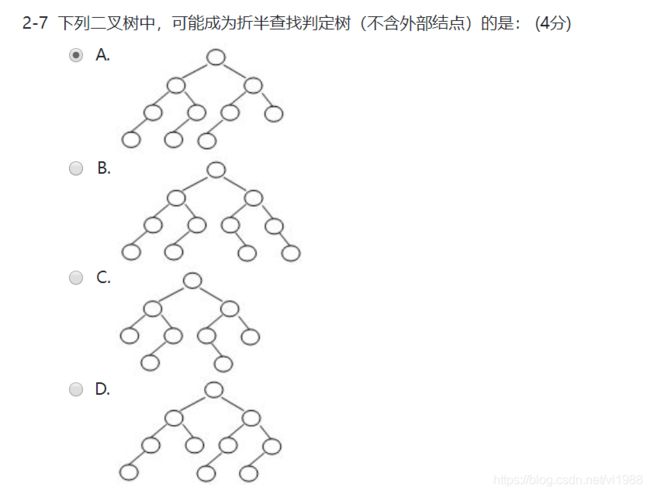
二叉搜索树的查找与树的形态有关，最差的情况是退化为单支树，（n+1）/2，N个节点的折半查找判定树是唯一的

查找不成功进行插入

二叉搜索树：或者唯一棵空树，或者是：若左子树不空，则左子树上的所有节点的值均小于根节点；若右子树不空，则右子树上所有的值均大于根节点，左右子树分别为二叉搜索树。  

可见其最大值为右子树为空的一个节点，即从根节点开始顺着右子树一直走到尽头，可能出现在最后一层，也可能出现在倒数第二层

 

2**4=16  有四层，比较次数，到最后一层时还需比较，才可以知道孩子为空判定不存在

分析同上，不存在，六层比较七次。

归并的趟数 O（logN）

希尔排序是不稳定的 ：由于多次插入排序，我们知道一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱，所以shell排序是不稳定的。对于排序算法，所谓的不稳定指的就是相同元素在排序过程中被移动；

14...问的是  归并的趟数，O（log n），  一趟归并排序的操作是：调用n/2h（向下取整）次merge（将两个有序的子序列归并为一个序列）将SR[1...n]中前后相邻且长度为n的有序段两两归并，得到前后相邻，长度为2h的有序段，并存放在TR[1..n]中，整个归并排序一共进行log2 n（向下取整，以二为底）趟。归并排序需要和待排记录等数量的辅助空间，时间复杂度O（nlogn）；

15  堆排序是就地排序，仅在堆顶元素与当前未经排序的子序列中最后一个元素交换时需要一个存储空间O（1）；

快速排序的平均时间为 knlnn,n为记录个数，在所有同数量级的此类排序算法中，快排的常数因子最小，被认为是最好的一种内部排序的方法，当初始记录基本有序，快排退化为冒泡排序，O(n**2);

每趟冒泡排序都会选出一个最大值放到未经排序序列最后，所以其位置经过一趟冒泡排序后确定，堆排序同理，每次都会选出未经排序的最大(最小)值，放入到未经排序序列最后，一趟快速排序完成后，枢轴元素位置确定，在分别对其左右递归进行，但是快排是不稳定的，不稳定性和这个题并没有直接关系，

快速排序有两个方向，左边的i下标一直往右走，当a[i] <= a[center_index]，
其中center_index是中枢元素的数组下标，一般取为数组第0个元素。而右边的
j下标一直往左走，当a[j] > a[center_index]。如果i和j都走不动了，
i <= j, 交换a[i]和a[j],重复上面的过程，直到i>j。 
交换a[j]和a[center_index]，完成一趟快速排序。在中枢元素和a[j]交换的
时候，很有可能把前面的元素的稳定性打乱，比如序列5 3 3 4 3 8 9 10 11，
现在中枢元素5和3(第5个元素，下标从1开始计)交换就会把元素3的稳定性打乱
，所以快速排序是一个不稳定的排序算法，不稳定发生在中枢元素和a[j]交换的时刻。

一趟插入排序完成后没有确定位置。

希尔排序就是跳跃性的直接插入排序，原理同上

归并排序占用的空间是最多的

比如：3 27 36 27，
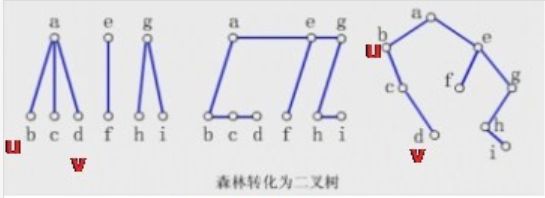
如果堆顶3先输出，则，第三层的27（最后一个27）跑到堆顶，然后堆稳定，继续输出堆顶，是刚才那个27，这样说明后面的27先于第二个位置的27输出，不稳定。

设F是一个森林，B是由F转换得到的二叉树，F中有n个非终端结点，B中右指针域为空的结点有?

解题思路

1. 设终端结点数为f，总结点数 f + n。每个结点有两个指针，总指针数 2（f + n）
2. 二叉树B除去根结点，都是某个结点的孩子， 也就是其余每个结点都有指针指向， 占用指针数为 f + n - 1；
3. 剩余空指针数为 2（f + n）- （f + n - 1）= f + n + 1 个
4. f 个终端结点没有孩子， 所以空的左指针域数为f 个；
5. 二叉树B 中右指针域为空的结点有 ( f + n + 1 ) - f = n + 1；

循环队列元素个数：(R-T+N)%N;

先序遍历序列和后序遍历序列正好相反：任意节点无右孩子

中序后序相同：无右子树

前序后序相同：只有根节点

前序中序相同：无左孩子    

分析方法：  前序：根 左 右  中序： 左 根 右  后序：左 右 根   也可以看出不同的遍历方法发生变化的是根节点的位置，所以叶 节点的相对次 序保持不变。

简单选择排  序不稳定性的原因

举个栗子  8 8 5 7 9  （从小到大）第一次选择 5 使得第一个8 和第二个8相对位置发生变化。 

快选希堆 不稳定