盖尔金圆定理(Gersghorin Circle Thorem)
盖尔金圆定理(Gersghorin Circle Thorem)是线性代数中一个有趣而实用的定理,可以用它来描述矩阵的特征值。首先我们先来看一下盖尔金圆定理。
(盖尔金圆定理)对于任意的$n$阶方阵$A$,若$\lambda$是$A$的一个特征值,则存在$1\leq i\leq n$,使得$|\lambda - a_{ii}| \leq \sum\limits_{j=1,j\neq i}^{n}|a_{ij}|.$
证明:
若$\lambda$是$A$的一个特征值,设其特征向量为$x$,可以选取$i$使得$|x_i|=\max\limits_{j=1,2,...,n} |x_{j}|=1,$这总是可以做到的,因为特征向量乘上任何数(除0外)仍为特征向量。
根据特征值和特征向量的定义,有$Ax=\lambda x$,因此有:
$$\sum\limits_{j=1}^{n}a_{ij}x_{j}=\lambda x_{i}.$$
从而:
$$|(\lambda-a_{ii})x_{i}|=|\lambda-a_{ii}|\leq \sum\limits_{j=1,j\neq i}^{n}|a_{ij}x_{j}|\leq \sum\limits_{j=1,j\neq i}^{n}|a_{ij}|.$$
证明完毕
对于任意一个方阵,我们只要画出它在复平面上的盖尔金圆,就能推测出特征值的分布情况了,因为该方阵的所有特征值总是在这些圆中某一个内。
下面给出如何在复平面上画方阵的盖尔金圆的Python代码,如下:
# Plotting Gershgorin Circles for any square matrix
from matplotlib.patches import Circle
import matplotlib.pyplot as plt
from math import sqrt
import numpy as np
# example matrix, each entity can be complex number
A = np.array([[5, 0, 0, -1],
[1, 0, -1, 0],
[-1.5, 1, -2, 1],
[-1, 1, 1, -3j]
],dtype='complex')
# begin plotting figure
fig = plt.figure()
ax = fig.add_subplot(111)
# Circle: |A[i,i]-z| <= sum(|A[i,j]| for j in range(n) and j != i)
for i in range(A.shape[0]):
real = A[i,i].real # each complex's real part
imag = A[i,i].imag # each complex's image part
# calculate the radius of each circle
radius = -sqrt(A[i,i].real**2+A[i,i].imag**2)
for j in range(A.shape[0]):
radius += sqrt(A[i,j].real**2+A[i,j].imag**2)
# add the circle to the figure and plot the center of the circle
cir = Circle(xy = (real,imag), radius=radius, alpha=0.5, fill=False)
ax.add_patch(cir)
x, y = real, imag
ax.plot(x, y, 'ro')
# title
plt.title("Gershgorin Circles of Matrix")
# show the figure which can be used for analyse eigenvalues of the matrix
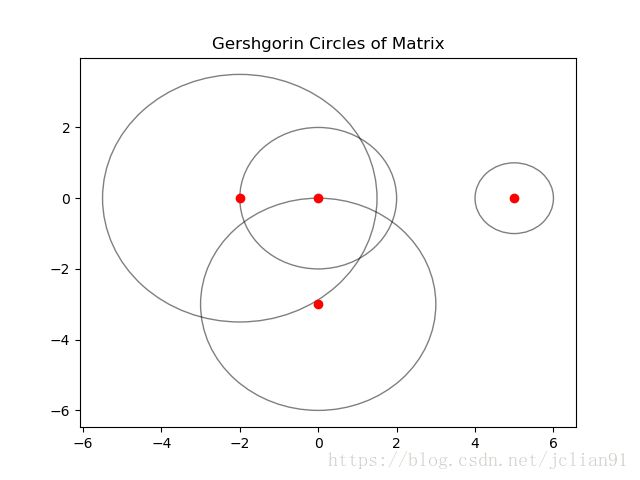
plt.savefig("E://GCircle.png")该方阵的盖尔金圆分布如下图:
以下给出盖尔金圆定理在 严格对角占优矩阵中的应用。
严格对角占优矩阵(SDD)
严格对角占优矩阵(Strictly Diagonally Dominant Matrix, SDD)是数值分析中的一个重要概念,它能保证Jacobi迭代法和Gauss-Seidel迭代法的收敛性。
所谓SDD,指的是满足以下条件的方阵:
$$|a_{ii}| > \sum\limits_{j=1,j \neq i}^{n}|a_{ij}|, \forall i =1,2,...,n.$$
通俗地来理解,就是主对角线上的每个元素的模(或者绝对值)都大于该元素所在行的所有元素(除掉它本身)的模(或者绝对值)的总和。
下面给出SDD的几个重要性质。
(SDD的性质)SDD必定是非奇异矩阵。
证明:若$A$为SDD,它不是非奇异矩阵,则$A$至少有一个特征值为0,从而由盖尔金圆定理可知,存在$1\leq i\leq n$,使得$|a_{ii}| \leq \sum\limits_{j=1,j\neq i}^{n}|a_{ij}|.$ 此与SDD的定义矛盾。从而SDD必定是非奇异矩阵。
(SDD的性质)若$A$为SDD,则$Ax=b$有解。
证明:因为$A$为SDD,故$A$可逆,从而$x=A^{-1}b.$
(SDD的性质)若$A$为SDD,则对于方程$Ax=b$, Jacobi迭代法, Gauss-Seidel迭代法,SOR迭代法收敛。
证明:因为我们还没讲到Jacobi迭代法, Gauss-Seidel迭代法,SOR迭代法,因此我们将在之后的博客中给出该性质的证明,敬请期待。