GRAAL

拓扑网络对齐揭示生物功能和发展史

摘要：序列比较和比对对我们对进化、生物学和疾病的理解产生了巨大的影响。生物网络的比较和比对可能会产生类似的影响。现有的网络比对使用网络外部的信息，例如序列，因为还没有设计出用于纯拓扑比对的好算法。在本文中，我们提出了一种完全基于网络拓扑的新算法，该算法可以用来对任意两个网络进行对齐。我们将其应用于生物网络，以产生迄今为止最完整的生物网络拓扑排列。我们证明，从我们的比对中可以提取出个体蛋白的物种系统发育和详细的生物学功能。基于拓扑的比对有可能提供一个全新的、独立的系统发育信息源。我们对两个非常不同的物种-酵母和人类-的蛋白质-蛋白质相互作用网络的比对表明，即使是遥远的物种也有惊人数量的网络拓扑结构，这表明地球上所有生命的内部细胞连接都有广泛的相似之处。

关键词：网络比对；蛋白质相互作用网络；网络拓扑；系统发育；蛋白质功能

1.介绍和动力

高通量实验方法的进步已经产生了大量的生物网络数据，如蛋白质-蛋白质相互作用(PPI)网络。两种最常用的高通量方法是酵母双杂交筛选，产生二元相互作用数据，以及使用质谱的蛋白质复合物纯化方法，产生共复合物数据 。正如比较基因组学导致关于进化、生物学和疾病的知识爆炸一样，比较蛋白质组学也将如此。随着越来越多的生物网络数据变得可用，跨物种的这些网络的比较分析被证明是有价值的，因为这种系统生物学类型的比较可能导致物种之间的知识转移，以及进化生物学中令人兴奋的发现。此类网络比较最常用的方法是网络对齐。

网络对齐是寻找两个或多个网络的结构或拓扑之间的相似性的问题。在生物学背景下，以有意义的方式比较不同生物的网络可以说是进化和系统生物学中最重要的问题之一。与基因组之间的序列比对完全相似，生物网络的比对可能是有用的，因为我们可能对一个网络中的一些节点了解很多，而对另一个网络中拓扑相似的节点几乎一无所知；然后，关于一个网络的专业知识可能会告诉我们一些关于另一个网络的新信息。网络比对也可以用来衡量不同物种的完整网络之间的全局相似性。给出一组这样的生物网络，成对的全局网络相似性矩阵可以用来推断系统发育关系。

1.1. 理论背景

网络(或图)是节点(或顶点)的集合，它们之间的连接称为边。图表被用来描述、建模和分析大量的现象，包括诸如电网和通信网络的物理系统、诸如友谊网络或公司和政治等级的社会系统、诸如折叠蛋白质中的残基相互作用的物理关系、或诸如呼叫图或表达和语法树的软件系统。

图G(V，E)，简称G，是有序对(V，E)，其中V是节点集，E是V×V是一个边集。可能图的绝对数量和多样性(给定n个结点，其中存在个)使得图的分类和比较问题变得困难。一个特殊的比较问题称为子图同构，它表示一个图G是否作为另一个图H(U，F)的精确子图存在。这个问题是NP完全的，这意味着没有已知的有效算法来解决它(Cook 1971)。网络对齐是更普遍的问题，即即使G不作为H的精确子图存在，也要找到最佳方式将G‘拟合’到H中。一些网络，例如我们下面考虑的生物网络，也可能包含噪声，即丢失边、伪边或两者兼而有之。在这些情况下，也由于生物变异，甚至不清楚如何衡量不精确拟合的“好坏”。一种度量可以是评估对齐的边的数量-即E中与F中的边对齐的边的百分比。我们称之为“边正确性”EC。然而，两条路线可能有相似的EC，其中一条暴露出G和H相似的大的、密集的、连续的和拓扑复杂的区域，而另一条未能暴露这样的相似区域。另外，虽然EC可以很容易地在事后衡量比对的质量，但如何使用它来指导比对算法并不清楚；实际上，最大化EC是一个NP-hard问题，因为它意味着解决子图同构问题。因此，必须寻求其他战略来指导调整进程。

1.2. 以前的方法

类似于序列比对，存在局部和全局网络比对。到目前为止，用于生物网络比对的大多数方法都集中在局部比对上。对于局部对齐，映射是针对每个相似的局部区域独立选择的。已经开发了许多局部比对算法。PathBLAST通过考虑对齐的蛋白质之间的同源性和路径中的PPI是真PPI而不是假的概率，来搜索两个网络之间的高得分路径比对。NetworkBLAST通过部署一种基于可能性的评分方案来检测保守的蛋白质簇而不是路径，该方案权衡了子网的密度与随机观察这种网络子结构的机会。MaWISh将网络比对定义为最大权重诱导子图问题，并实现了基于进化的评分方案来检测保守的簇；它将序列比对中的进化事件的概念扩展到网络比对中的复制、匹配和失配的概念，并通过考虑这些进化事件的计分函数来评估网络结构之间的相似性。GRAEMLIN是第一种能够识别任意结构的密集保守子网络的方法，它通过计算模块受到进化限制的概率和模块不受限制的概率的对数比来对模块进行评分，同时考虑到其网络被比对的物种之间的系统发育关系。

局部对齐可以是模棱两可的，其中一个节点在不同的局部对齐中具有不同的配对。相比之下，全局网络对齐提供从较小网络中的每个节点到较大网络中恰好一个节点的唯一对齐，即使这可能导致某些局部区域中的非最佳匹配。以前的局部网络对齐算法通常不能识别在进化过程中被保守的大的子图。

全球网络对齐之前已经在生物网络的背景下进行了研究。与上述主要以检测保守子网络为目标的算法不同，ISORANK旨在最大限度地提高两个网络之间的整体匹配度。它依靠谱图理论来计算来自不同网络的节点对的比对得分；它是通过使用启发式算法来实现的，即如果两个节点各自的邻居也匹配得很好，那么两个节点就是很好的匹配。因此，蛋白质对的分数取决于邻居的分数，而邻居的分数又取决于邻居的分数，以此类推。一旦为所有节点对计算了这些“拓扑”分数，基于序列的BLAST分数就被包括在成对比对分数中。然后，ISORANK用重复贪婪策略构建节点比对，该策略在所有蛋白质对中识别得分最高的对，输出该对，并移除涉及两个识别的节点中的任何一个的所有分数。最近的ISORANKN依赖于特定节点排名的概念，并使用类似于PageRank-Nibble算法的方法。GRAEMLIN已经被扩展为通过依赖学习算法来允许全球网络比对，该学习算法使用已知网络比对及其系统发生关系的训练集来学习用于其评分函数的参数，并且通过自动使所学习的目标函数适应于任何网络集合。

1.3. 我们的贡献

所有以前的算法充其量只能隐含地或间接地依赖于网络的拓扑，因为它们严重依赖于关于节点的一些先验信息，例如PPI网络中蛋白质的序列相似性(§3.2)。序列是非常有价值的生物信息来源。由于蛋白质聚集在一起执行某种功能，而不是孤立地作用，因此对PPI网络中围绕蛋白质的复杂连接进行系统水平的分析也可以提供有价值的生物学信息，并深入了解细胞的内部工作。网络拓扑和蛋白质序列可能提供对生物信息互补能力。例如，存在相同的蛋白质序列，可以在不同的环境中以不同的方式折叠，导致不同的功能和PPI网络拓扑。在这种情况下，在网络拓扑中比在序列相似性中更正确地编码同源信息。因此，如果只关注序列，可能会丢失这些信息。我们提出了一种网络对齐算法，其代价函数完全显式地基于一个强的、理论上有根据的、直接的网络拓扑相似性度量。由于我们的方法不使用蛋白质序列信息，它可以比对任何两个网络，而不仅仅是生物网络。例如，我们的算法可以应用于道路地图或社会网络，它们显然没有与之相关的基因或蛋白质序列。请注意，如果我们试图理解复杂的生物现象，我们应该尝试使用所有可用的生物数据，包括序列和拓扑。这是因为集成不同的数据源可以提供更深层次的理解。因此，我们设计我们的方法的方式是允许将序列信息包括到比对成本函数中(见§2)。然而，仅从网络拓扑中就可以提取多少生物信息是非常重要的。因此，我们的研究解决了寻找一个完全依赖于网络拓扑的好的网络对齐算法的问题。

我们将我们的方法应用于两个PPI网络的比对，并证明了我们的比对比现有方法暴露了更复杂的拓扑相似区域。此外，我们还利用我们的方法计算了一组物种之间的两两全对网络相似性矩阵，然后构建了与基于序列比较的系统发育树非常相似的系统发育树。这些结果的重要之处在于，它们从一种新的生物信息源--纯网络拓扑中提取生物知识，独立于任何其他生物信息源。我们认为，本文的结果仅仅触及了可以从网络拓扑中提取的信息的皮毛。

2.材料和方法

图G(V，E)，简称G，有结点集V和边集E。给定n=|V|个结点，无向边的最大数目为M=n*(n-1)/2，因此n个结点上可能的无向图的数目为2^M。可能图的绝对数量和多样性使得图的分类和比较问题变得困难。其中一个问题称为子图同构：给定两个任意图G(V，E)和H(U，F)，使得|V|<|U|，G是否作为H的子图存在？也就是说，有没有离散映射：V->U,这个问题是NP完全的，这意味着没有已知的有效算法来寻找映射-唯一已知的普遍适用的方法是搜索从V到U的所有可能的映射(Cook 1971)。由于这种映射的数量在|V|和|U|中都是指数的，因此这被认为是一个难以解决的问题

2.1. Graphlet度特征和特征相似性

GRALL根据本地邻居的相似性度量对源自不同网络的一对节点进行比对。对于所有2-5个节点的Graphlet，此度量将计算节点接触的边数的节点度数概括为Graphlet度向量，计算节点接触的Graphlet的数量(参见图1)。请注意，节点的度数是此向量中的第一个坐标，因为边(图1中的G0)是唯一的2节点Graphlet。由于区分例如在末端或中间接触字形G1的节点在拓扑上是相关的，所以使用自同构轨道(或者为了简单起见，仅仅是轨道)的概念。考虑到小图形的节点之间的“对称性”，所有2到5个节点的小图形有73个不同的轨道。我们将轨道编号从0到72。73个坐标的全向量是节点的特征(图2)。

节点的特征为其附近的局部拓扑提供了一种新颖且高度约束的度量，而比较两个节点的特征则提供了两个节点之间局部拓扑相似性的高度约束度量。特征相似度计算如下。对于节点u∈G，ui表示其特征向量的第i个坐标，即ui是节点u被G中的轨道i触及的次数。节点u和v的第i个轨道之间的距离Di(u，v)定义为其中，wi是轨道i的权重，它考虑了轨道之间的依赖关系；例如，轨道3的计数的差异将意味着包含三角形的所有轨道的计数的差异，如轨道10-14、25、26等，因此，分配给轨道3、w3的权重高于包含它的轨道。节点u和v之间的总距离D(u，v)定义为：D(u,v)=距离D(u，v)在[0，1]中，其中距离0表示节点u和v的特征相同。最后，节点u和v之间的特征相似度S(u，v)为

2.2. GRAAL(图形对齐器)算法

当对齐两个图G(V，E)和H(U，F)时，Graal首先计算将G中的每个节点v与H中的每个节点u对齐的成本。对齐两个节点的成本考虑了它们之间的特征相似度，由于具有相似特征的较高度节点提供了比相应相似的低度节点更严格的约束(参见电子辅助材料1)，因此随着两个节点的度的增加而修改以降低成本。通过这种方式，我们首先对齐网络中最密集的部分。如果我们用 deg（v） 表示网络 G 中的节点 v 的度，由 max_deg(G):G 中节点的最大程度,S(v，u):节点 v 的特征相似性以及α用 [0， 1] 中的参数表示，该参数控制节点特征相似性对成本函数的贡献（也就是说， 1-α 是控制节点度对成本函数的贡献的参数，然后将节点 v 对齐的成本计算为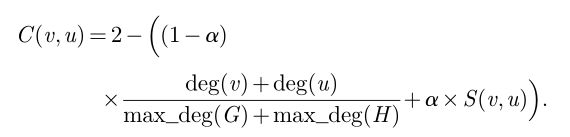。开销0对应于一对拓扑相同的节点v和u，而接近2的开销对应于一对拓扑不同的节点。

还可以将蛋白质序列分量添加到代价函数中，以在排列节点的拓扑相似性和序列相似性之间进行平衡。这可以通过向成本函数添加另一个参数b来简单地实现，该参数β将控制当前拓扑导出的成本的贡献，而1-β将控制节点序列相似性对总成本函数的贡献；在其他相关研究中已经使用了类似的方法因此，如果 S'（v，u） 是节点 v 和u之间的序列相似性，则通过包括序列相似性获得的节点 v 和您获得的新成本可以计算为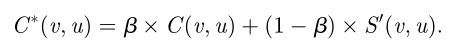然而，由于我们的目标是只提取在网络拓扑中编码的生物信息，分析拓扑和序列相似性之间的平衡如何影响最终的比对超出了我们的讨论的范围，并且是未来工作的主题。
Graal选择具有最小成本的一对节点(v，u)、v∈V和u∈U作为初始种子。种子是随机选取的，这可能会在不同的运行中导致不同的对齐，尽管我们的经验表明，在不同的运行中，大约60%的整个对齐是一致的(§3.2)。一旦找到种子，Graal就会在节点v和u周围建立所有可能半径的“球体”。围绕结点v的半径为r的球面是距v的距离r的结点集SG(v，r)=，其中距离d(v，x)是从v到x的最短路径的长度。然后，两个网络中半径相同的球体通过搜索尚未对齐且可以以最小成本对齐的配对，将两个网络中相同半径的球体贪婪地对齐在一起当种子(v，u)周围的所有球体都已对齐时，两个网络中的一些节点可能保持未对齐。出于这个原因，Graal在一对网络(G^P、H^P)上对p=1、2和3重复相同的算法，并在必要时再次搜索新的种子。我们定义一个网络G^P=(V,E^p),作为一个具有与G相同的结点集和唯一的（v，x)∈E^p的新的网络Gp,G中节点v和x之间的距离小于或等于p，即请注意，G1=G。使用GP，p=1允许我们将一个网络中长度为p的路径与另一个网络中的单个边对齐，这类似于允许在序列比对中进行“插入”或“删除”。当G中的每个节点恰好与H中的一个节点对齐时，Graal停止。

Graal生成全局对齐。我们注意到最佳的全局比对不一定是唯一的。给定任何特定的成本函数，可能会有许多不同的路线，所有这些路线都共享最优成本。在这篇文章中，我们只分析了一个我们认为是好的特定排列，尽管它可能不是最优的，即使根据我们的衡量标准。枚举所有最优(或者至少是好的)比对需要扩展我们的算法以允许两个网络中的节点之间的多对多映射，这是未来工作的主题。因此，可能会有更多与本文同等有效性的预测成为可能。然而，我们的经验证明，整个比对的很大一部分(约60%)在算法的不同运行中是保守的；因此，这种核心比对与算法中的随机性无关。

电子补充资料中给出了算法的伪代码和复杂度分析的详细内容。本文中使用的软件和数据可根据需要提供。

2.3. 我们的酵母-人类比对的统计学意义

给定两个网络G(V，E)和H(U，F)的粗对齐，我们随机计算获得给定或更好的边正确分数的概率。为此，需要一个适当的随机对齐零模型。随机对齐是两个网络中的节点之间的随机映射fGraal生成全局对齐，以便较小网络中的所有节点(就节点数量而言较小)与较大网络中的节点对齐。换言之，f定义为这等效于将G(V，E)中的每条边与H(U，F)中的一对节点(不一定是一条边)对齐。因此，我们将随机比对的零模型定义为随机映射g:我们定义了n1=|V|、n2=|U|、m1=|E|和m2=|F|。我们还定义H中节点对的个数为p=n2(n2-1)/2，并设EC=x%为给定排列的EC。我们让k=[m1*EC]=[M1*x]是G中与H中的边对齐的边数。因此，偶然成功对齐k条或更多条边的概率P是超几何分布的尾部：对于我们的酵母2-人1比对，我们发现P≈7*10^8。

现在，我们描述了如何估计我们在比对中发现的yeast2和Human 1之间的相似性的统计意义。要做到这一点，我们需要估计人们期望在两个随机网络之间找到多少相似之处，而要做到这一点，反过来又需要我们指定如何生成模型随机网络。给出两个声称符合一组观测的模型，我们通常认为可调参数较少的模型更优越。例如，构造粘性模型和ER-DD模型以保持数据的度分布。因此，这些和其他数据驱动的随机网络模型(Snijders2002；Thorne&Stumpf2007；Kuchaiev&PrzˇUlj2009)有望比理论网络模型更好地模拟特定的ppi网络。然而，它们不是判断yeast2和Human 1网络是否具有显著的结构相似性的合适选择；这是因为这些模型强烈地依赖于这些特定的网络，因此它们可能会将我们首先旨在检测的yeast2和Human 1之间的相似性转移到模型网络上。因此，我们寻找一个很好的理论零模型。可以说，当前已知的用于ppi网络的最好的、需要最少可调参数的理论模型是几何随机图模型(‘geo’；PRZˇUlj等人)。2004年；PRZˇUlj，2007年；Higham等人。2008)，其中蛋白质被建模为存在于公制空间中，并且如果它们彼此在固定的、指定的距离内，则由一条边连接。

尽管早期不完整的PPI数据集由于其幂律程度分布而被无尺度网络很好地建模,有人争辩说，这样的学位分布是噪音的产物.根据新的购买力平价网络数据，几项研究(PrzˇUlj et al.。2004年；PRZˇUlj，2007年；Higham等人。2008)提出了令人信服的证据，证明PPI网络的结构更接近几何而不是无标度网络。这是通过比较现实世界和模型网络中的小图形的频率来实现的，并通过测量“石墨线度分布”之间的高度约束性一致性(PRZˇULJ2007)。最后，证明了PPI网络可以成功地嵌入到低维欧几里德空间中，从而直接证实了它们具有几何结构(Higham et al.。2008)。GEO模型比其他模型更适合PPI网络，这可能并不令人惊讶，因为它可以是生物动机的。我们的直觉是基于对基因(和蛋白质作为基因产物)存在于某些生化空间的观察。目前公认的范式是基因组通过一系列基因复制和突变事件进化(Ohno 1970)。这可以在上述生化空间中按如下方式建模。当一个基因被复制时，它的孩子在生化空间中处于相同的位置。然后，自然选择作用于复制的基因，使其中一个基因从另一个基因转移到生化空间(通过突变)。突变水平越大，生化空间的距离越大。因此，重复的基因在空间上越接近，共同相互作用的伙伴的数量就越多。这些过程自然可以由地球观测组织模拟(见PRZ、ˇ、ULJ等人)。有关详细信息，请参阅2010)。除了PPI网络，GEO对于其他生物网络，例如脑功能网络，是一个很好的理论零模型(Kuchaiev等人。2009)一个蛋白质结构网络(Milenkovic‘et al.。(2009年)。

接受GEO作为PPI网络的最优零模型，我们计算出在我们的yeast2和Human1比对中获得11.72%的EC的概率为8.4*10^-3。为此，我们将yeast2和Human 1大小相同的GEO网络的Graal对进行比对，并应用以下形式的Vysochanskij-Petunin不等式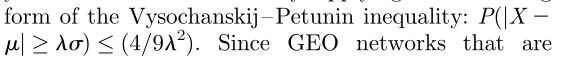：由于已对齐的GEO网络具有与数据相同的节点和边数，因此可以合理地假设其对齐分数的分布是单峰的。因此，我们使用Vysochanskij-Petunin不等式，因为对于单峰分布，它比Chebyshev不等式更精确。电子补充材料中提供了更多详细信息。

3.结果与讨论

显然，如果要仅基于网络拓扑建立有意义的比对，则必须首先具有高度约束性的拓扑相似性度量。节点拓扑的最简单描述是它的度数，即接触它的边数。我们更具约束性的度量是节点度数的泛化。我们将图形定义为一个更大的网络的小型、连接的、诱导的子图。G的节点集X∈V上的导出子图是通过取X和G的所有在X中具有两个端节点的边来获得的。图1示出了2、3、4和5个节点上的所有小图形。对于大型网络中的特定节点v，我们定义了一个‘Graphlet度’的向量(Milenkovic‘&PrzˇUlj2008)，它计算接触v的每种Graphlet的数量(图2)。V的这个向量或特征描述了其邻域的拓扑结构，并捕获了距离为4的范围内的互连性(见§4.1和图2；Milenkovic‘&PrzˇUlj2008)。由于这种测量是基于所有多达5个节点的小图形，因此由于它们的小世界性质，它在量化许多真实世界网络中节点之间的局部拓扑相似性方面非常有效(Watts&Stogue atz 1998)。

就我们的目的而言，两个网络G和H的比对由一组有序对(x，y)组成，其中x是G中的一个节点，y是H中的一个节点。我们的算法称为GRAAL(Graph Aligner)，它结合了局部比对和全局比对的各个方面。我们基于源自不同网络的节点对的签名相似性来匹配它们(ˇ和PRZ Milenkovic‘&Prz Milenkovic’&Prz Milenkovic Ulj2008)，其中两个节点之间的特征相似性越高，它们的扩展邻域之间的拓扑相似性就越高(超出距离4)。对齐两个节点的成本被修改为首先对齐网络中最密集的部分；成本随着两个节点的度的增加而降低，因为具有相似签名的较高度节点提供了比相应类似的低度节点更严格的约束(参见§2和电子补充材料)；α是[0，1]中的一个参数，它控制节点签名相似度对代价函数的贡献，另一个贡献仅仅是节点的程度(见§2)。在两个节点对齐相等的情况下，将随机打破平局。因此，对齐算法的不同运行可以产生不同的结果。然而，我们发现，对于我们下面分析的PPI网络，包含所有对齐的60%的确定性“核心”比对在所有运行中保持不变(见§3.2)。

我们将较小网络中的每个节点与较大网络中的一个节点对齐。匹配使用类似于流行的BLAST的“种子和扩展”方法的技术进行(Altschul等人。(1990)序列比对算法：我们首先选择具有高签名相似度的单个“种子”节点对(来自每个网络的一个节点)。然后，我们使用贪婪算法(见§2)尽可能地在种子周围径向向外扩展比对。虽然我们的算法本质上是局部的，但是我们的算法产生了大而密集的全局比对。我们所说的“密集”是指对齐子图共享许多边，这在低质量或随机对齐中不会是这种情况。

3.1. 对Graal算法的评价

为了测量Graal的性能，我们对齐了高置信度酵母PPI网络的最大连通组件(Collins等人。2008)，由1004种蛋白质之间的8323个相互作用组成，通过(1)从网络中随机移除节点；(2)从网络中随机移除边；(3)向网络中随机添加边；以及(4)向网络中添加低置信度PPI(因此，这是向网络中添加真实数据，但是该数据是低置信度)，从而获得其合成的(或有噪声的)对应物。对于这四种“噪音类型”中的每一种，我们都用不同百分比的附加噪音进行实验：5%、10%、15%、20%和25%。由于随机性，我们每个实验运行30次，平均结果超过30次。例如，对于上述类型(1)和5%噪声水平的实验，我们通过从数据网络中随机移除5%的节点来随机化数据30次；这导致30个随机化网络，并且我们将它们中的每一个与原始数据网络对齐，以获得我们平均的30个EC分数。唯一的例外是上面的噪声类型(4)，添加了低置信度PPI：该噪声类型不存在随机性，因为添加了来自较低置信度数据集的前k%最具置信度的PPI(k？5、10、15、20、25)。结果显示在电子补充材料中，图S7和S8。通过这些测试，根据噪声类型和级别，我们证明了我们的算法能够产生高质量的比对，EC约为90%(参见电子补充材料的“Graal算法评估”一节，图S7和S8)。这表明，在给定对齐网络拓扑相似性较高的情况下，我们的算法能够发现具有较高EC的对齐。

3.2. 酵母与人PPI网络的配对比对

使用Graal，我们比对了Radivojac等人的人类PPI网络。(2008)给Collins等人。(2008)酵母PPI网络，我们分别称其为“人1”和“酵母2”。我们选择酵母作为我们的第二个物种，因为目前它拥有一个高质量的PPI网络，2390个蛋白质(节点)之间有16127个相互作用(边)。Graal找到的“最佳”对齐方式(定义如下)将yast2中的1890条边与Human 1中的边对齐。因此，我们一致的EC是11.72%。这些“正确”的边缘对齐涉及970个节点，占所有Yast2节点的40%。我们获得了相似的EC，用于比对其他酵母(Stark等人。2006年；Collins等人。2008)和人类(Peri等人。2004年；Rual等人。2005年；Stark等人。2006年)网络(见电子补充材料，图S1)。最佳对齐定义如下。由于成本函数中a参数的存在(如上所述)和Graal算法中的一些随机性(详见§2.2和电子补充材料)，实际的比对和ECs在不同的a值和同一a的算法的不同运行中不同。考虑到这一点，最好的对齐是对a的所有值和给定a的所有运行的最高EC的对齐。最高的 EC是在a为0.8的情况下获得的；此a的所有运行的最小EC高于0和1之间的任何其他a的所有运行的最大EC，增量为0.1。因此，我们将重点放在为0.8生成的路线上。不同运行阶段的EC变化很小，最小EC为11.5%，最大EC为11.72%。此外，最多40条不同路线以0.8的比率相交的路线包含1433对路线，约占整条路线的60%。我们称这个交叉口为核心路线。

除了计算对齐的边之外，重要的是将对齐的边聚集在一起以形成大而密集的连通子图，以便发现这种相似拓扑的区域。我们将公共连通子图(CCS)定义为出现在两个网络中的连通子图(不一定是诱导的)。我们最佳比对中最大的CCS(图3a)在267个蛋白质之间有900个相互作用，占酵母2网络中蛋白质的11.2%。我们的第二大CCS在52个节点之间有286个交互，如图3b所示。整个公共子图显示在电子补充材料中，如图S2所示。

3.3. 格拉尔(氏)酵母-人配对的质量

优化EC是一个NP-hard问题，因此我们不能肯定地说，对于我们分析的酵母和人类PPI网络，11.72%的EC是否是最大EC。然而，由于我们在合成数据上证明了Graal可以正确地比对相似的网络(§3.1)，我们相信Graal与远距离物种(如酵母和人类)的PPI网络之间11.72%的EC的比对是好的。我们通过证明这种比对的统计学意义和生物学有效性来进一步支持这一信念(见下文)。此外，我们还表明，我们的比对的大小和质量都优于竞争方法产生的比对(见§3.4)。

我们看了几种不同的方法来判断Graal的酵母-人类比对的质量。首先，将其拓扑性与这两个特定网络的随机比对进行比较，判断其拓扑性。我们发现，在酵母和人类PPI网络的随机比对中获得11.72%或更好(p值)的EC的概率低于71028(有关我们使用的随机比对的零模型的详细信息，请参见§2.3和电子补充材料)。获得大CCS的概率会小得多，因此这表示我们的p值有一个弱的上界。

其次，我们评论了在Graal比对中发现的酵母和人类之间的拓扑相似性的数量。我们将Graal的酵母-人类比对与Graal的与数据大小相同的随机网络(来自特定模型)的比对进行了比较。如果我们与来自几个不同的随机图模型的Graal网络保持一致(Milenkovic‘et al.。我们发现，随机网络间的EC最多为8.8±0.39%，明显低于Graal的Yast2-Human 1比对的EC 11.72%，p值小于8.4？1023(如下所述)。结果表明，随机网络间的EC最多为8.8±0.39%，明显低于Graal的Yast2-Human 1比对的EC 11.72%，p值小于8.4？1023(如下所述)。具体来说，对齐两个 Erdo +s =re'nyi 随机图形与数据（'ER-DD'）的度分布相同，仅给出约 0.31±0.22% 的 EC。巴拉巴西-阿尔伯特型无标度网络(“SF-BA”；巴拉巴西和阿尔伯特1999年)、粘性模型网络(“Sticky”；PRZˇUlj&Higham 2006)或三维几何随机图(“GEO-3D”；PRZˇUlj等人)的类似排列。2004年)，EC得分分别为2.86±0.57、5.89±0.39和8.8±0.39%。即使我们使用五个不同的网络模型作为零模型，我们只报告了酵母和人的Graal比对的p值，当与GEO作为零模型进行评估时。这不仅是因为GEO已经被证明是PPI网络的最佳拟合模型(参见§3)，还因为当Graal将GEO与GEO网络(数据大小)进行比对时，并且当我们使用这些比对来计算Graal酵母-人类比对的统计显著性时，我们得到的p值比使用其他四个网络模型中的任何一个时都要高。因此，我们选择空模型，这是评估GRAAL酵母的统计符号-人类对齐的最坏情况，我们仍然得到p的值8.4*10^-3.这告诉我们，酵母和人类这两个非常不同的物种，享有比偶然情况下更多的网络相似性。

第三，我们通过检查是否：(I)排列的蛋白质对执行相同的生物学功能；(Ii)Graal能够识别进化保守的功能模块；以及(Iii)Graal的酵母和人类的排列是由序列比对支持的，来分析我们排列的生物学性质。

• 我们计算我们排列的对中有多少共享共同的基因本体论(GO)术语(基因本体论联盟2000)。GO术语简明扼要地描述了给定蛋白质可能具有的许多生物学特性。对于这个分析，我们考虑独立于GO证据代码的“完整的”GO注释数据集，它包含所有的GO注释。GO注释数据于2009年9月下载。在我们最好的酵母2-人1比对中，45.1%、15.6%、5.1%和2.0%的比对蛋白质对分别共享至少一个、两个、三个和四个围棋术语。与随机排列相比，这些百分比的p值均在1026至1028范围内。此外，在Graal的核心酵母2-人1比对中，结果有所改善：50.9%、19.3%、7.3%和3.0%的比对蛋白质对分别共享至少一个、两个、三个和四个GO项；这些百分比的p值都在10^-8到10^-9的范围内。

• 我们发现，Graal将酵母和人类的网络区排列在一起，其中很大比例的蛋白质在这两个物种中发挥着相同的生物学功能。在“最佳”比对中(在§2.2中定义)，Graal比对了酵母和人类之间的52个节点子网络，其中98%的酵母和67%的人类蛋白质参与剪接。这一结果令人鼓舞，因为已知即使在遥远的真核生物之间剪接也是保守的(Wentz-Hunter&Potashkin 1995；Collins&Penny 2005；Lorkovic等人)。2005)。此外，它还比对了一个24节子网络，其中96%的酵母和39%的人类蛋白质参与转录。此外，它还比对了另一个12节子网络，其中25%的酵母和40%的人类蛋白质参与转录。最后，它比对了一个10个节点的子网，在这个子网中，100%的酵母和80%的人类蛋白质参与了翻译。对于“核心”比对(在§2.2中定义)也得到了类似的结果：Graal比对了一个48节子网络，其中98%的酵母和69%的人类蛋白质参与剪接；此外，它还比对了一个12节子网络，其中25%的酵母和40%的人类蛋白质参与转录。

• 我们检查了Graal的酵母和人类PPI网络的核心比对，我们发现19%的比对的酵母-人类蛋白质对的序列同一性超过了进化相关性的“暮光区”阈值30%(Doolite1981；Rost 1999)。Rost(1999)分析了蛋白质数据库中100多万个蛋白质序列的比对，发现序列同一性超过这个阈值的比对蛋白质对中有90%是同源的。此外，在Graal的核心比对中，大约70%的蛋白质对在“黄昏地带”具有序列同一性，即20%到30%之间。虽然不能肯定地宣称在“黄昏地带”具有同一性的序列具有进化上的相似性(杜利特尔，1981；Rost，1999)，但绝大多数同源物的序列同一性已被证明不到30%。因此，Graal的酵母-人类比对似乎部分地得到了序列比对的支持。

第2节和电子补充材料提供了有关上述所有内容的更多详细信息。

3.4. 与其他方法的比较

Graal产生了迄今为止最完整的生物网络拓扑排列，并发现了比目前发表的算法产生的CCS大得多、密度更高的CCSS，如下所示。目前发表的类似网络的最佳全球比对是酵母和苍蝇的ISORANK比对(Singh等人。2007)，其除了使用拓扑信息之外还使用序列信息。它对齐1420条边，但其最大的CCS只包含35个节点和35条边。我们仅使用拓扑信息将ISORANK应用于我们的yeast2-Human 1数据。我们发现，它对齐了628个交互，边缘正确率仅为3.89%，而Graal的EC为11.72%。因此，我们比ISORANK多对齐三倍的边。ISORANK最大的CCS在116种蛋白质之间只有261个相互作用，而Graal的最大CCS在267个蛋白质之间有900个相互作用。因此，就节点数量和边数而言，Graal最大的CCS分别比ISORANK最大的CCS大2.3倍和3.5倍。注意，我们没有在ISORANK的比对成本函数中包括序列信息，因为Singh等人。(2007)已经证明，当单独使用拓扑时，可以获得最高的EC。

此外，尽管Graal没有使用任何蛋白质序列信息，但在共享GO术语的数量方面，我们的结果比ISORANK取得的结果要好。在ISORANK产生的全球比对中，44.2%、14.1%、4.1%和1.5%的比对蛋白质对分别具有至少一个、两个、三个和四个GO术语，而Graal的比例分别为45.1%、15.6%、5.1%和2.0%。此外，如果我们的分析仅限于最大的CCS，在ISORANK的CCS中，共享至少1个、2个和3个常见GO术语的百分比分别为60.6%、11.9%和0%，而在Graal的CCS中，这些百分比分别为67.2%、22.0%和5.2%。

最近，一种用于多网络全局比对的算法ISORANKN被引入(Liao et al.。(2009年)。然而，与Graal进行比较是不可行的，因为两种算法的输出是不同的。GRAAL输出待比对网络之间的一对一节点映射列表，而ISORANKN的比对包含多组比对蛋白质，其中没有两组重叠，但每组可以包含来自每个比对网络的多个节点(即多对多节点映射)。因此，ISORANKN的输出不能用EC在拓扑上量化，因为一个多对多节点对齐可以产生指数级的多个一对一节点对齐，并且枚举所有这些节点对齐在计算上是不可行的。

另一种流行的全球网络对齐方法是GRAEMLIN(Flannick等人，2008)。我们没有将我们的比对与GRAEMLIN产生的比对进行比较，因为GRAEMLIN需要各种其他输入信息，包括被比对的物种之间的系统发育关系。相比之下，格拉尔的研究结果可以用来推断系统发育关系。

最后，存在可能比ISORANK更好的其他方法(Zaslatski等人)。(2009年)。然而，他们目前的实现无法处理Yast2和Human 1大小的网络(M.Zaslatski和J.-P.Vert，2009，与作者的个人交流)。此外，我们没有在扎斯拉夫斯基等人分析的酵母和苍蝇数据上对这些方法进行基准测试。(2009)，因为他们没有试图比对整个酵母和苍蝇网络，但他们只专注于他们定义的较小的诱导亚图，这些亚图定义在由副妄想症簇覆盖的蛋白质上。因此，尽管它们的“全局”酵母-苍蝇比对将较小子网(如上定义)中的每个节点与较大子网中的一个节点对齐，但它并不是真正的全局，因为它只对齐了原始酵母和苍蝇网络的一部分。因此，我们发现用部分酵母和苍蝇网络的“全球”比对来评估Graal对整个酵母和苍蝇网络的全球比对是不合适的。此外，我们认为一个好的网络比对算法应该既能产生高质量的比对，又能处理大数据集；对于生物网络尤其如此，因为它们的规模只会继续增长。因此，扎斯拉夫斯基等人的方法。(2009)未能处理任何较大数据集的数据与我们考虑的大型网络无关。

3.5.。在蛋白质功能预测中的应用

有了以上的验证(§3.3)，我们相信Graal的比对可以根据未注释蛋白质与注释蛋白质的比对来预测其生物学特性(即GO分子功能(MF)、生物过程(BP)和细胞组分(CC))。

这里，我们区分两组不同的GO注释数据：上面描述的完整集，包含所有围棋注释，独立于GO证据代码，以及基于生物的集合，包含仅通过实验证据代码获得的围棋注释(详细信息见Gene Ontology Consortium(2000))。由于在完整的GO注释数据集中，许多GO项是通过计算(例如，根据序列比对)分配给蛋白质的，因此该集在生物学上的置信度低于基于生物学的集。我们对这两个GO注释数据集进行预测，如下所述。

首先，我们分析了Graal的最佳酵母2-人1比对(即在所有运行中α为0.8时与最高EC的比对，如§2中所解释的)，以确定已比对的蛋白质对，其中一个蛋白质仅用“根”GO术语注释：GO：0003674(MF)，GO：0008150(BP)，或GO：0005575(CC)；这意味着对中的一个蛋白质没有已知的功能信息(Gene Ontology Consortual2000)。接下来，我们检查关于完整的和基于生物的GO注释数据集，这些功能未知的蛋白质的排列伙伴是否用已知的MF、BP或CC GO术语进行了注释。如果是这样的话，我们将所有已知的MF、BP或CC GO术语指定给未注释的蛋白质。

对于完整的GO数据集，我们预测44个人类和435个酵母蛋白的MF，53个人类和157个酵母蛋白的BP，52个人类和54个酵母蛋白的CC。由于围棋数据库提供了一个带有明确注释的列表，即蛋白质与给定的围棋术语没有关联，因此我们能够直接检查我们的预测是否与该列表相矛盾。我们在GO数据库中没有发现与MF或BP相关的任何酵母或人类蛋白的矛盾；我们只发现我们关于CC的一个人类预测有矛盾。我们还试图使用文献搜索和文本挖掘工具CITEXPLORER(Labarga等人)来验证我们所有的预测。(2007年)。对于34.1%、43.4%和46.2%的MF、BP和CC人类预测，该工具发现至少有一篇文章在我们对该蛋白质的至少一个预测的上下文中提到了感兴趣的蛋白质。对于酵母，这三个百分比分别为42.07%、3.18%和12.96%。我们对完整的GO数据集所做的人类和酵母预测分别出现在电子补充材料表S1和S2中。

对于基于生物的GO数据集，我们预测30个人蛋白和214个酵母蛋白的MF，42个人蛋白和41个酵母蛋白的BP，45个人蛋白和17个酵母蛋白的CC。这些预测在围棋数据库中都没有矛盾。我们用CITEXPLORER分别验证了我们基于生物学的MF、BP和CC人类预测的10%、4.76%和20%。我们还验证了48.1%的基于生物学的MF酵母预测。我们对基于生物的GO数据集所做的人类和酵母预测分别出现在电子补充材料表S3和S4中。

3.6.。通过比对跨物种的代谢途径重建系统发育树

最后，我们描述了一个完全不同的应用：如何使用Graal获得的代谢网络的纯拓扑比对来恢复系统发育关系。

图4通过基因序列比对和格拉尔新陈代谢网络比对获得的原生生物系统发育树的比较。左图：遗传序列比对得到的树。右图：从格拉尔那里得到的那棵树。以下缩写用于种的缩写：CHO，人隐孢子虫；DDI，盘基网柄菌；CPV，隐孢子虫细小；P F A，恶性疟原虫；EHI，溶组织内阿米巴；TAN，环状泰勒虫；TPV，微小泰勒虫。这些物种被分成以下几类：“泡状菌”、“内阿米巴”和“细胞黏菌”。

一些分析不同物种代谢途径的研究旨在发现物种之间的进化关系，并构建它们的系统发育树(Forst&Schulten 2001；Heymann&Singh 2003；Suthram等人)。2005；Zhang et al.。(2006年)。不同的距离度量被用于构建系统发育树。例如，根据相应底物和来自单个途径的酶之间的序列相似性(Forst&Schulten 2001)或者作为来自单个代谢网络的酶的相似性和这些网络的拓扑的组合来计算途径之间的相似性(Heymann&Singh 2003；Suthram等人)。2005)。酶的相似性是基于它们的序列、结构或酶委员会编号的相似性(Webb 1990)。两条路径的拓扑相似性一直基于节点之间的相似性(对应于酶)及其邻域的相似性，衡量一个节点是否影响相似的节点，以及它是否受到相似节点本身的影响(Heymann&Singh 2003)。此外，代谢途径的拓扑相似性结合了全局网络属性，如直径和聚类系数，以及共享节点(即酶)邻域的相似性(Zhang等人。(2006年)。

因此，尽管存在相关尝试(Suthram等人，2005)，它们都仍然使用网络拓扑之外的一些生物或功能信息，例如序列相似性，来定义节点相似性，并从路径中推导出系统发生树。因为我们只使用网络拓扑来定义蛋白质相似性，所以我们的信息源是根本不同的。因此，我们的算法以一种完全新颖和独立的方式恢复了系统发育关系(但不是物种分化的进化时间尺度)，而不是所有现有的系统发育恢复方法。

研究表明，PPI网络结构对蛋白质的进化有微妙的影响，合理的系统发育推断只能在密切相关的物种之间进行(Agrafioti等人)。2005)。在KEGG途径数据库中，有17种真核生物具有全序列(Kanehisa&Goto 2000)，其中7种是原生生物，6种是真菌，2种是植物，2种是动物。这里我们关注的是原生生物(参见真菌的电子补充材料)。对于每个生物体，我们从KEGG中提取所有代谢途径的联合体，然后使用Graal找出物种之间所有对所有的成对网络比对。两对原生生物网络之间的EC得分从29.6%到76.7%不等。我们使用平均距离算法创建系统发育树，2以成对的EC作为距离度量。我们将我们的系统发育树与通过基因或氨基酸序列比对获得的已发表的系统发育树3进行比较(Keling等人。2000年；Pennisi 2003)。图4展示了我们的原生动物系统发育树，并表明它与通过序列比较发现的非常相似(Pennisi 2003)。我们可以通过测量我们的树与由与新陈代谢网络相同大小的随机网络构建的树进行比较来估计树的统计意义；我们发现我们树的p值小于1.3？1023。基于ISORANK所作比对的系统发育树与随机树没有显著不同(见电子补充资料)。我们还发现微小隐孢子虫和人隐孢子虫整个代谢网络的拓扑结构非常相似，EC为75.72%。这一结果令人鼓舞，因为这些生物是Apicomplexan原生动物的两个形态相同的物种，具有97%的遗传序列同一性，但宿主截然不同(Tanriverdi和Widmer，2006年)，这是造成它们分歧的原因(Xu等人)。2004)。

请注意，我们对齐的所有新陈代谢网络都是从实验获得的数据和基于物种间同源关系的网络重建的混合中衍生出来的。因此，我们在很大程度上恢复了从序列比对中获得的系统发育树，这一事实有力地验证了我们的方法。此外，文献中的系统发育树是通过线粒体蛋白质或核糖体RNA的序列比对获得的，而KEGG中的代谢网络部分是通过蛋白质序列的序列比对获得的。因此，由于文献中用于重建系统发育树和重建代谢网络的序列数据来源不同，从我们的网络比对获得的系统发育树可能已经被视为新的和独立的系统发育信息源。当纯实验获得的网络变得可用时，这将获得生物学上的重要性，进一步提供基于序列的系统发育的验证。

鉴于我们的系统发育树与序列产生的系统发育树略有不同，没有理由相信基于序列的系统发育树应该先验地被认为是正确的。基于序列的系统发育树是基于基因序列的多重比对和全基因组比对而构建的。由于发生在亚串水平的基因重排、倒置、转位和易位，多重比对可能具有误导性。此外，不同物种的基因或基因组的数量可能不同，长度也有很大的不同。由于基因的非连续拷贝或非决定性的基因序列，全基因组系统发育分析也可能具有误导性(Out&Sayood，2003)。最后，树是由概率地“拼凑”在一起的较小片段递增构建的(Pennisi 2003)，因此树中的概率错误是可以预期的。我们的树没有这些问题，但它可能会受到其他问题的影响，如噪声和PPI网络的不完备性。

4.结论

综上所述，我们提出的证据表明，仅从网络拓扑中提取生物知识是可能的。提出了一种完全基于网络拓扑的全局网络对齐算法。因此，它可以应用于任何网络类型，而不仅仅是生物网络类型。我们应用我们的方法来比对酵母和人类的PPI网络，并证明了它产生了具有拓扑统计意义的比对，在这些比对中，许多比对的蛋白质执行相同的生物功能。鉴于我们的酵母-人类比对的高质量，我们基于其注释的比对伙伴的功能来预测未注释蛋白质的生物学功能，验证了我们在文献中的大量预测。此外，我们成功地从代谢网络的拓扑比对中重建了系统发育树，证明了网络拓扑可以作为一种新的、独立的系统发育信息来源。

网络对齐在从社交网络到软件调用图的众多领域都有应用。在生物领域，目前可用的网络数据只会继续增加，我们相信高质量的拓扑比对可以产生对功能、进化和疾病的新的关键见解。

REFERENCES

Agrafioti, I., Swire, J., Abbott, J., Huntley, D., Butcher, S. &
  Stunpf, M. P. 2005 Comparative analysis of the Saccharo-
  myces cerevisiae and Caenorhabdits elegans protein
  interaction networks. BMC Evol. Biol. 5.
Altschul, S. F., Gish, W., Miller, W. & Lipman, D. J. 1990
  Basic local alignment search tool. J. Mol. Biol. 215,
  403–410.
Baraba ´si, A. & Albert, R. 1999 Emergence of scaling in
  random networks. Science 286, 509–512. (doi:10.1126/
  science.286.5439.509)
Berg, J. & Lassig, M. 2004 Local graph alignment and motif
  search in biological networks. Proc. Natl Acad. Sci. USA
  101, 14 689–14 694. (doi:10.1073/pnas.0305199101)
Berg, J. & Lassig, M. 2006 Cross-species analysis of biological
  networks by Bayesian alignment. Proc. Natl Acad. Sci.
  USA 103, 10 967–10 972. (doi:10.1073/pnas.0602294103)
Colizza, V., Flammini, A., Serrano, M. A. & Vespignani, A.
  2006 Detecting rich-club ordering in complex networks.
  Nat. Phys. 2, 110–115. (doi:10.1038/nphys209)
Collins, S., Kemmeren, P., Zhao, X., Greenblatt, J., Spencer,
  F., Holstege, F., Weissman, J. & Krogan, N. 2008 Toward
  a comprehensive atlas of the physical interactome of
  Saccharomyces cerevisiae. Mol. Cell. Proteom. 6, 439–
  450. (doi:10.1074/mcp.M600381-MCP200)
Collins, L. & Penny, D. 2005 Complex spliceosomal organiz-
  ation ancestral to extant eukaryotes. Mol. Biol. Evol. 22,
  1053– 1066. (doi:10.1093/molbev/msi091)
Cook, S. 1971 The complexity of theorem-proving procedures.
  Proc. 3rd Annu. ACM Symp. Theory of Computing,
  pp. 151–158. New York, NY: Association for Computing
  Machinery.
de Silva, E., Thorne, T., Ingram, P., Agrafioti, I., Swire, J.,
  Wiuf, C. & Stumpf, M. P. 2006 The effects of incomplete
  protein interaction data on structural and evolutionary
  inferences. BMC Biol. 4.
Doolittle, R. F. 1981 Similar amino-acid sequences: chance or
  common ancestry? Science 214, 149–159. (doi:10.1126/
  science.7280687)
Flannick, J., Novak, A., Balaji, S., Harley, H. & Batzglou, S.
  2006 GRAEMLIN general and robust alignment of multiple
  large interaction networks. Genome Res. 16, 1169 –1181.
  (doi:10.1101/gr.5235706)
Flannick, J., Novak, A. F., Do, C. B., Srinivasan, B. S. &
  Batzoglou, S. 2008 Automatic parameter learning for
  multiple network alignment. In Proc. Int. Conf. Research
  in  Computational  Molecular  Biology—RECOMB,
  pp. 214–231.
Forst, C. & Schulten, K. 2001 Phylogenetic analysis of
  metabolic pathways. J. Mol. Evol. 52, 471–489.
Gavin, A. C. et al. 2002 Functional organization of the yeast
  proteome by systematic analysis of protein complexes.
  Nature 415, 141– 147. (doi:10.1038/415141a)
Gavin, A. C. et al. 2006 Proteome survey reveals modularity
  of the yeast cell machinery. Nature 440, 631–636.
  (doi:10.1038/nature04532)
Guimera, R., Sales-Pardo, M. & Amaral, L. A. N. 2007 Classes
  of complex networks defined by role-to-role connectivity
  profiles. Nat. Phys. 3, 6 3–69 . (doi:10.1038/nphys489)
Han, J. D. H., Dupuy, D., Bertin, N., Cusick, M. E. & Vidal,
  M. 2005 Effect of sampling on topology predictions of
  protein–protein interaction networks. Nat. Biotechnol.
  23, 839–844. (doi:10.1038/nbt1116)
Heymans, M. & Singh, A. 2003 Deriving phylogenetic trees
  from the similarity analysis of metabolic pathways. Bioinfor-
  matics 19, i 1 3 8 – i 1 4 6 . (doi:10.1093/bioinformatics/btg1018)
Higham, D., Ras ˇajski, M. & Prz ˇulj, N. 2008 Fitting a geo-
  metric graph to a protein –protein interaction network.