卡尔曼滤波系列(五)——奇异值鲁棒的卡尔曼滤波算法
目录
- 1 简介
- 2 原理
- 3 实验
- 4 参考文献
1 简介
传统的卡尔曼滤波算法假定了噪声服从高斯分布,而实际应用场景中,由于传感器受到各种因素的影响,可能存在部分远偏离预期值的观测结果,称为奇异值。此时观测噪声不再是高斯分布的,而类似于student-t分布,对于这样的情况,传统的卡尔曼滤波算法在估计系统状态时会极大地受到奇异值带来的影响,从而导致系统状态估计结果远偏离预期,此时需要对卡尔曼滤波做一些调整,使其能适用于非高斯的噪声分布。
2 原理
首先有状态转移方程和观测方程如下,与标准卡尔曼滤波中的形式一致。
θ k = A θ k − 1 + s k z k = C θ k + v k {{\bf{\theta }}_k} = {\bf{A}}{{\bf{\theta }}_{k - 1}} + {{\bf{s}}_k} \\ {{\bf{z}}_k} = {\bf{C}}{{\bf{\theta }}_k} + {{\bf{v}}_k} θk=Aθk−1+skzk=Cθk+vk
其中 θ k {\bf{\theta }}_k θk表示第 k {k} k时刻的系统状态, z k {\bf{z}}_k zk表示对 k {k} k时刻系统状态的观测结果,而 A \bf{A} A和 C \bf{C} C分别代表状态转移矩阵和观测矩阵,另外 s k {\bf{s}}_k sk为状态噪声, s k ∼ N ( 0 , Q ) {{\bf{s}}_k}\sim N\left( {{\bf{0}},{\bf{Q}}} \right) sk∼N(0,Q), r k {{\bf{r}}_k} rk为观测噪声, r k ∼ N ( 0 , R / w k ) {{\bf{r}}_k}\sim N\left( {{\bf{0}},{\bf{R}}/w_k} \right) rk∼N(0,R/wk),权重 w k ∼ G a m m a ( a , b ) {{w}_k}\sim Gamma\left( {a,b} \right) wk∼Gamma(a,b)。这里 Q ∈ R N × N {\bf{Q}} \in {\mathbb{R}^{N \times N}} Q∈RN×N是一个对角阵,对角线上的元素为 q ∈ R N × 1 {\bf{q}} \in {\mathbb{R}^{N \times 1}} q∈RN×1, R ∈ R M × M {\bf{R}} \in {\mathbb{R}^{M \times M}} R∈RM×M也是一个对角阵,对角阵上的元素为 r ∈ R M × 1 {\bf{r}} \in {\mathbb{R}^{M \times 1}} r∈RM×1。
对于标准的卡尔曼滤波而言,矩阵 Q {\bf{Q}} Q和矩阵 R {\bf{R}} R表征的是状态噪声和观测噪声的协方差,而卡尔曼滤波算法的最终状态估计,说到底就是根据矩阵 Q {\bf{Q}} Q和矩阵 R {\bf{R}} R的值去权衡系统的估计偏向预测和偏向观测的程度。举个例子,如果矩阵 Q {\bf{Q}} Q远大于 R {\bf{R}} R矩阵 ,也就是说状态噪声十分剧烈,相对的观测噪声很小,那么系统的估计就非常接近观测的结果;反之矩阵 Q {\bf{Q}} Q远小于矩阵 R {\bf{R}} R,也就是说观测噪声相当大,相对的状态噪声很小,那么系统的状态估计就更多地偏向于根据上一个时刻的状态估计所预测的当前时刻系统状态。
我们可以将这样的模型及求解模型的问题视为期望最大化(EM)学习问题,然后通过最大化对数似然函数,学习这些变量的值。有似然函数为
ln p ( θ 0 : k , z 1 : k , w 1 : k ) = ∑ i = 1 k ln p ( z i ∣ θ i , w i ) + ∑ i = 1 k ln p ( θ i ∣ θ i − 1 ) + ln p ( θ 0 ) + ∑ i = 1 k ln p ( w i ) = 1 2 ∑ i = 1 k ln w i − k 2 ln ∣ R ∣ − k 2 ln ∣ Q ∣ − 1 2 ∑ i = 1 k w i ( z i − C θ i ) T R − 1 ( z i − C θ i ) − 1 2 ∑ i = 1 k ln w i − 1 2 ∑ i = 1 k [ θ i − A θ i − 1 ] T Q − 1 [ θ i − A θ i − 1 ] − 1 2 ln ∣ Q 0 ∣ − 1 2 ( θ 0 − θ ^ 0 ) Q 0 − 1 ( θ 0 − θ ^ 0 ) + ∑ i = 1 k a ln w i − ∑ i = 1 k b w i + c o n s t \ln p({{\bf{\theta }}_{0:k}},{{\bf{z}}_{1:k}},{w_{1:k}}) = \sum\limits_{i = 1}^k {\ln } p\left( {{{\bf{z}}_i}|{{\bf{\theta }}_i},{w_i}} \right) + \sum\limits_{i = 1}^k {\ln } p\left( {{{\bf{\theta }}_i}|{{\bf{\theta }}_{i - 1}}} \right) + \ln p\left( {{{\bf{\theta }}_0}} \right) + \sum\limits_{i = 1}^k {\ln } p\left( {{w_i}} \right) \\ = \frac{1}{2}\sum\limits_{i = 1}^k {\ln {w_i}} - \frac{k}{2}\ln \left| {\bf{R}} \right| - \frac{k}{2}\ln \left| {\bf{Q}} \right| - \frac{1}{2}\sum\limits_{i = 1}^k {{w_i}{{\left( {{{\bf{z}}_i} - {\bf{C}}{{\bf{\theta }}_i}} \right)}^T}{{\bf{R}}^{ - 1}}\left( {{{\bf{z}}_i} - {\bf{C}}{{\bf{\theta }}_i}} \right)} \\- \frac{1}{2}\sum\limits_{i = 1}^k {\ln } {w_i} - \frac{1}{2}\sum\limits_{i = 1}^k {{{\left[ {{{\bf{\theta }}_i} - {\bf{A}}{{\bf{\theta }}_{i - 1}}} \right]}^T}{{\bf{Q}}^{ - 1}}\left[ {{{\bf{\theta }}_i} - {\bf{A}}{{\bf{\theta }}_{i - 1}}} \right]} - \frac{1}{2}\ln \left| {{{\bf{Q}}_0}} \right| \\- \frac{1}{2}\left( {{{\bf{\theta }}_0} - {{{\bf{\hat \theta }}}_0}} \right){\bf{Q}}_0^{ - 1}\left( {{{\bf{\theta }}_0} - {{\widehat {\bf{\theta }}}_0}} \right) + \sum\limits_{i = 1}^k {a\ln {w_i}} - \sum\limits_{i = 1}^k b {w_i} + {\rm{const}} lnp(θ0:k,z1:k,w1:k)=i=1∑klnp(zi∣θi,wi)+i=1∑klnp(θi∣θi−1)+lnp(θ0)+i=1∑klnp(wi)=21i=1∑klnwi−2kln∣R∣−2kln∣Q∣−21i=1∑kwi(zi−Cθi)TR−1(zi−Cθi)−21i=1∑klnwi−21i=1∑k[θi−Aθi−1]TQ−1[θi−Aθi−1]−21ln∣Q0∣−21(θ0−θ^0)Q0−1(θ0−θ 0)+i=1∑kalnwi−i=1∑kbwi+const
我们可以从正态和Gamma分布的标准形式中得出最终的EM更新方程,即对于当前时间步 k {k} k,有如下算法:
E-Step:
Σ k = ⟨ w k ⟩ ( C k T R k − 1 C k + Q k − 1 ) − 1 {{\bf{\Sigma }}_k} = \left\langle {{w_k}} \right\rangle {\left( {{\bf{C}}_k^T{\bf{R}}_k^{ - 1}{{\bf{C}}_k} + {\bf{Q}}_k^{ - 1}} \right)^{ - 1}} Σk=⟨wk⟩(CkTRk−1Ck+Qk−1)−1
⟨ θ k ⟩ = Σ k ( Q k − 1 A k ⟨ θ k − 1 ⟩ + ⟨ w k ⟩ C k T R k − 1 z k ) \left\langle {{{\bf{\theta }}_k}} \right\rangle = {{\bf{\Sigma }}_k}\left( {{\bf{Q}}_k^{ - 1}{{\bf{A}}_k}\left\langle {{{\bf{\theta }}_{k - 1}}} \right\rangle + \left\langle {{w_k}} \right\rangle {\bf{C}}_k^T{\bf{R}}_k^{ - 1}{{\bf{z}}_k}} \right) ⟨θk⟩=Σk(Qk−1Ak⟨θk−1⟩+⟨wk⟩CkTRk−1zk)
⟨ w k ⟩ = a + 1 2 b + 1 2 ( z k − C θ k ) T R k − 1 ( z k − C θ k ) \left\langle {{w_k}} \right\rangle = \frac{{a + \frac{1}{2}}}{{b + \frac{1}{2}{{\left( {{{\bf{z}}_k} - {\bf{C}}{{\bf{\theta }}_k}} \right)}^T}{\bf{R}}_k^{ - 1}\left( {{{\bf{z}}_k} - {\bf{C}}{{\bf{\theta }}_k}} \right)}} ⟨wk⟩=b+21(zk−Cθk)TRk−1(zk−Cθk)a+21
M-Step:
C k = ( ∑ i = 1 k ⟨ w i ⟩ z i ⟨ θ i ⟩ T ) ( ∑ i = 1 k ⟨ w i ⟩ ⟨ θ i θ i T ⟩ ) − 1 {{\bf{C}}_k} = \left( {\sum\limits_{i = 1}^k {\left\langle {{w_i}} \right\rangle {{\bf{z}}_i}} {{\left\langle {{{\bf{\theta }}_i}} \right\rangle }^T}} \right){\left( {\sum\limits_{i = 1}^k {\left\langle {{w_i}} \right\rangle } \left\langle {{{\bf{\theta }}_i}{\bf{\theta }}_i^T} \right\rangle } \right)^{ - 1}} Ck=(i=1∑k⟨wi⟩zi⟨θi⟩T)(i=1∑k⟨wi⟩⟨θiθiT⟩)−1
A k = ( ∑ i = 1 k ⟨ θ i ⟩ ⟨ θ i − 1 ⟩ T ) ( ∑ i = 1 k ⟨ θ i − 1 θ i − 1 T ⟩ ) − 1 {{\bf{A}}_k} = \left( {\sum\limits_{i = 1}^k {\left\langle {{{\bf{\theta }}_i}} \right\rangle {{\left\langle {{{\bf{\theta }}_{i - 1}}} \right\rangle }^T}} } \right){\left( {\sum\limits_{i = 1}^k {\left\langle {{{\bf{\theta }}_{i - 1}}{\bf{\theta }}_{i - 1}^T} \right\rangle } } \right)^{ - 1}} Ak=(i=1∑k⟨θi⟩⟨θi−1⟩T)(i=1∑k⟨θi−1θi−1T⟩)−1
r k m = 1 k ∑ i = 1 k ⟨ w i ⟩ ⟨ ( z i m − C k ( m , : ) θ i ) 2 ⟩ {r_{km}} = \frac{1}{k}\sum\limits_{i = 1}^k {\left\langle {{w_i}} \right\rangle \left\langle {{{\left( {{{\bf{z}}_{im}} - {{\bf{C}}_k}(m,:){{\bf{\theta }}_i}} \right)}^2}} \right\rangle } rkm=k1i=1∑k⟨wi⟩⟨(zim−Ck(m,:)θi)2⟩
q k n = 1 k ∑ i = 1 k ⟨ ( θ i n − A k ( n , : ) θ i − 1 ) 2 ⟩ {q_{kn}} = \frac{1}{k}\sum\limits_{i = 1}^k {\left\langle {{{\left( {{{\bf{\theta }}_{in}} - {{\bf{A}}_k}(n,:){{\bf{\theta }}_{i - 1}}} \right)}^2}} \right\rangle } qkn=k1i=1∑k⟨(θin−Ak(n,:)θi−1)2⟩
其中 r k m {r_{km}} rkm表示向量 r k {{\bf{r}}_k} rk的第 m m m个元素, q k n {q_{kn}} qkn表示向量 q k {{\bf{q}}_k} qk的第 n n n个元素, a a a和 b b b是先验的Gamma分布的尺度参数,当 k k k时刻的传感器采样结果获得时,便可以进行上述的算法。
⟨ w k ⟩ \left\langle {{w_k}} \right\rangle ⟨wk⟩的计算公式中, θ k {{\bf{\theta }}_k} θk的值可以用上一个时刻的估计结果 ⟨ θ k − 1 ⟩ \left\langle {{{\bf{\theta }}_{k - 1}}} \right\rangle ⟨θk−1⟩ 所预测的当前时刻状态值 θ k ′ = A ⟨ θ k − 1 ⟩ {\bf{\theta }}_k^{'}{\rm{ = }}{\bf{A}}\left\langle {{{\bf{\theta }}_{k - 1}}} \right\rangle θk′=A⟨θk−1⟩代替。也就是说,权值 ⟨ w k ⟩ \left\langle {{w_k}} \right\rangle ⟨wk⟩近似的与误差 的平方成反比,假定 时刻的状态估计 是符合预期的,那么如果 时刻的传感器观测出现奇异值的话,误差 就会取大值,因此权值 很小,进而观测噪声的协方差矩阵就会很小,根据卡尔曼滤波的原理,对当前时刻的状态做估计时,结果会更偏向于预测而比较不会被观测到的奇异值所影响。
另外,算法对矩阵 Q {\bf{Q}} Q和矩阵 R {\bf{R}} R的初始值设置较为敏感,其值应该根据观测数据的噪声情况设定,例如对于观测噪声较大的数据,可以取值为 Q = R = 0.01 I {\bf{Q}}{\rm{ = }}{\bf{R}} = 0.01{\bf{I}} Q=R=0.01I,对于观测噪声较小的数据,可以取初始值为 Q = R = 0.0001 I {\bf{Q}}{\rm{ = }}{\bf{R}} = 0.0001{\bf{I}} Q=R=0.0001I,其中 I {\bf{I}} I表示单位阵。
以上算法与卡尔曼滤波的关系可以通过联合两个算法的公式获得,因此奇异值鲁棒的卡尔曼滤波算法也可以通过下列公式计算:
预测:
θ k ′ = A k ⟨ θ k − 1 ⟩ {\bf{\theta }}_k^ {'}= {{\bf{A}}_k}\left\langle {{{\bf{\theta }}_{k - 1}}} \right\rangle θk′=Ak⟨θk−1⟩
Σ k ′ = Q k {\bf{\Sigma }}_k^{'}= {{\bf{Q}}_k} Σk′=Qk
更新:
S k = ( C k Σ k ′ C k T + 1 w k R k ) − 1 {{\bf{S}}_k} = {\left( {{{\bf{C}}_k}{\bf{\Sigma }}_k^{'}{\bf{C}}_k^T + \frac{1}{{{w_k}}}{{\bf{R}}_k}} \right)^{ - 1}} Sk=(CkΣk′CkT+wk1Rk)−1
K k = Σ k ′ C k T S k {{\bf{K}}_k} = {\bf{\Sigma }}_k^{'}{\bf{C}}_k^T{{\bf{S}}_k} Kk=Σk′CkTSk
⟨ θ k ⟩ = θ k ′ + K k ( z k − C k θ k ′ ) \left\langle {{{\bf{\theta }}_k}} \right\rangle = {\bf{\theta }}_k^{'} + {{\bf{K}}_k}\left( {{{\bf{z}}_k} - {{\bf{C}}_k}{\bf{\theta }}_k^{'}} \right) ⟨θk⟩=θk′+Kk(zk−Ckθk′)
Σ k = ( I − K k C k ) Σ k ′ {{\bf{\Sigma }}_k} = \left( {{\bf{I}} - {{\bf{K}}_k}{{\bf{C}}_k}} \right){\bf{\Sigma }}_k^{'} Σk=(I−KkCk)Σk′
在进行上述算法之前,可以先用EM算法估计各个参数的值,包括其中的权值 w k {w_k} wk,当观测出现奇异值时, w k {w_k} wk的参数估计结果就会很小,于是矩阵 S k {{\bf{S}}_k} Sk的值就会减小,从而导致卡尔曼增益 K k {{\bf{K}}_k} Kk减小,于是 K k ( z k − C k θ k ′ ) {{\bf{K}}_k}\left( {{{\bf{z}}_k} - {{\bf{C}}_k}{\bf{\theta }}_k^{'}} \right) Kk(zk−Ckθk′)就会减小,最终导致系统状态的估计结果偏向于 θ k ′ {\bf{\theta }}_k^{'} θk′,即对当前时刻的状态预测值 θ k ′ = A k ⟨ θ k − 1 ⟩ {\bf{\theta }}_k^{'} = {{\bf{A}}_k}\left\langle {{{\bf{\theta }}_{k - 1}}} \right\rangle θk′=Ak⟨θk−1⟩。
3 实验
在12自由度(DOF)机器狗上评估了所有滤波器,如下图所示。该机器狗有两个测量其方向的信号源:运动捕获(MOCAP)系统和机载惯性测量 单位(IMU)。两者都提供了机器人方向的四元数q:来自MOCAP的qMOCAP和来自IMU的qIMU。由于IMU无法提供稳定的方向估计,但其信号干净,因此qIMU随时间漂移。 在IMU中发生的漂移在传感器收集需要集成的数据的系统中非常普遍。相比之下,qMOCAP具有奇异值和噪声,但没有漂移。我们想估计qMOCAP和qIMU之间的偏移,该偏移是一个包含奇异值的有噪声的缓慢漂移信号。
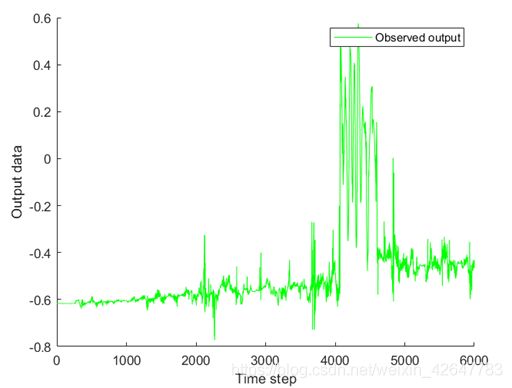
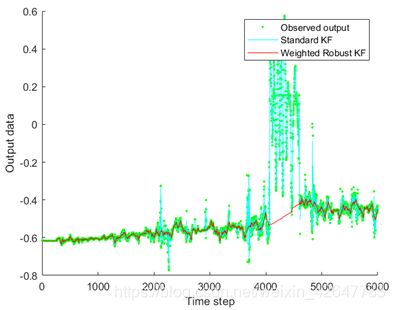
图中可以看出,观测结果随机出现偏离正常波动范围的奇异值,传统的卡尔曼滤波算法并不具有检测奇异值的功能,观测到奇异值时,算法认为该时刻的观测仍然是有效的,认为奇异值反映了系统状态出现了较大的改变,所以给出了偏离正常范围的系统状态估计结果。而实际上,奇异的观测并非系统状态的有效反映,而是噪声出现离群值,对于这样的噪声,奇异值鲁棒的加权卡尔曼滤波算法通过结合上一个时刻的状态估计以及当前时刻的观测结果,计算权值,并在估计当前时刻的状态时,用该权值修正新息,抑制奇异值的影响,从而获得更鲁棒的估计结果。
4 参考文献
[1] . Joanne Ting,Evangelos Theodorou,Stefan Schaal. A Kalman Filter for Robust Outlier Detection. 2008
原创性声明:本文属于作者原创性文章,小弟码字辛苦,转载还请注明出处。谢谢~
如果有哪些地方表述的不够得体和清晰,有存在的任何问题,亦或者程序存在任何考虑不周和漏洞,欢迎评论和指正,谢谢各路大佬。
有需要相关技术支持的可咨询QQ:297461921
