Reinforcement_Learning
文章目录
- 2 基础概念
- 2.1 数据与标签
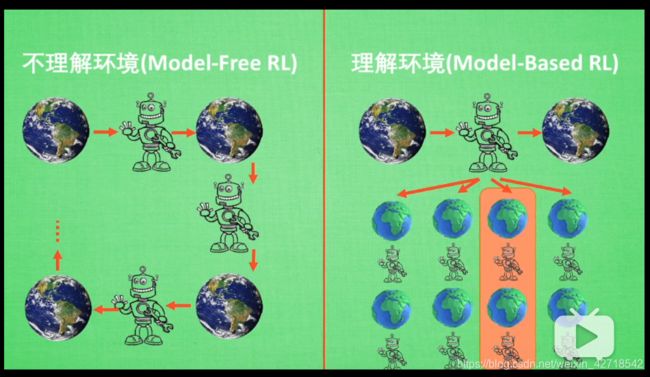
- 3 强化学习分类
- 3.1 基于概率与基于价值
- 3.2 回合更新与单步更新
- 3.3 在线学习与离线学习
- 4 对照一个实际的例子,完全参考他人代码(非原创)编程实现了一个简单的QLearning案例,理解了代码的意思
- 4.1 动画项目图解
- 4.2 伪代码
- 4.3 伪代码与真实代码结合
- 4.4 总代码
- 5 Sarsa
- 6 最大熵
- Policy-based
- policy-based实战
- PPO proximal policy optimization
文章中含有参考文献,若有侵权,请联系本人删除
2 基础概念
2.1 数据与标签
3 强化学习分类
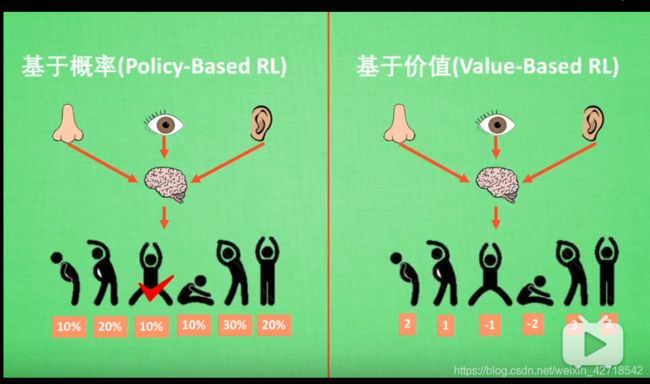
3.1 基于概率与基于价值
- 基于概率:即使某个时间发生概率最高,我们也不一定选它
- 基于价值:死脑筋,就选价值最高的
- 对于离散的动作,俩者都可以选
- 对于连续的动作,基于价值就无能为力了
3.2 回合更新与单步更新
3.3 在线学习与离线学习
- 离线学习: 可以看着别人学,学到经验就行; 或者白天自己学习,然后晚上通过离线学习来复习(我觉得人性化一点)
- 在线学习: 只能当场在线学习
4 对照一个实际的例子,完全参考他人代码(非原创)编程实现了一个简单的QLearning案例,理解了代码的意思
4.1 动画项目图解
4.2 伪代码
4.3 伪代码与真实代码结合
# Initialize Q(s,a) arbitrarily
q_table = build_q_table(N_STATES, ACTIONS)
# Repeat (for each episode):
for episode in range(MAX_EPISODES):
# Initialize s
S = 0 # 点的位置,
# Repeat (for each step of episode):
while not is_terminated:
# Choose a(action) from s(state) using policy derived from Q (e.g. ,e-greedy)
A = choose_action(S, q_table)
# take action a, observe r, s_next
S_, R = get_env_feedback(S, A)
q_predict = q_table.loc[S, A]
q_target = R + LAMBDA * q_table.iloc[S_, :].max()
q_table.loc[S, A] += ALPHA * \
(q_target - q_predict) # update the current Q_Table
S = S_ # move to next state
4.4 总代码
import numpy as np
import pandas as pd
import time # 控制探索者移动速度有多快
np.random.seed(2) #
N_STATES = 6
ACTIONS = ['left', 'right'] # 要不走左边, 要不走右边
EPSILON = 0.9
ALPHA = 0.1
LAMBDA = 0.9
MAX_EPISODES = 13 # 只玩13回合, 因为13个回合已经可以训练的很好了
FRESH_TIME = 0.01 # 控制探索者移动速度有多快,走一步花0.3秒(如果想让他走慢点,就变为1.0)
# 建立Q表
def build_q_table(n_states, actions):
table = pd.DataFrame(
np.zeros((n_states, len(actions))), # q_table initial values, 全部初始化为0
columns=actions,
)
# print(table)
return table
# 决策过程
def choose_action(state, q_table):
# This is how to choose an action
state_actions = q_table.iloc[state, :] # 提取行号==state的这一行的所有数据
if (np.random.uniform() > EPSILON) or (state_actions.all() # act non-greedy or state-action
== 0): # >EPSILON,eg:EPSILON=0.9, >0.9表示只有%10的几率
action_name = np.random.choice(ACTIONS) # %10的几率是随机选择(往左走,往右走)
else: # act greedy
action_name = state_actions.argmax() # %90的可能是选择这一行所有数据的最大值
return action_name
def get_env_feedback(S, A):
# This is how agent will interact with the environment
if A == 'right': # move right
if S == N_STATES - 2: # terminate ,为啥是 N_STATES-2, 无法理解
S_ = 'terminal'
R = 1 # 只有到达了终点, R(奖励,reword)才能是1,只有寻找到了终点的宝藏, 奖励才为1
else:
S_ = S + 1 #
R = 0 # 没有到达终点, R永远是0,
else: # move left
R = 0
if S == 0:
S_ = S # reach the wall,此时为开始的位置 state==0,
else:
S_ = S - 1 # 不是开始的位置的时候,此时向左走, 因此S_(下一步) = S( 当前状态(离起点的步数) ) -1
return S_, R
# 环境框架,知道即可,不用深入探究
def update_env(S, episode, step_counter):
# This is how environment be updated
env_list = ['-'] * (N_STATES - 1) + ['T'] # '---------T' our environment
if S == 'terminal':
interaction = 'Episode %s: total_steps = %s' % (
episode + 1, step_counter)
print('\r{}'.format(interaction), end='')
time.sleep(2)
print('\r ', end='')
else:
env_list[S] = 'o'
interaction = ''.join(env_list)
print('\r{}'.format(interaction), end='')
time.sleep(FRESH_TIME)
def rl():
# main part of RL loop
q_table = build_q_table(N_STATES, ACTIONS)
for episode in range(MAX_EPISODES):
step_counter = 0
S = 0 # 点的位置,
is_terminated = False
update_env(S, episode, step_counter)
while not is_terminated:
A = choose_action(S, q_table)
# take action & get next state and reward
S_, R = get_env_feedback(S, A)
q_predict = q_table.loc[S, A]
if S_ != 'terminal':
# next state is not terminal
q_target = R + LAMBDA * q_table.iloc[S_, :].max()
else:
q_target = R # next state is terminal
is_terminated = True # terminate this episode
q_table.loc[S, A] += ALPHA * \
(q_target - q_predict) # update the current Q_Table
S = S_ # move to next state
update_env(S, episode, step_counter + 1)
step_counter += 1
return q_table
if __name__ == "__main__":
q_table = rl()
print('\r\nQ-table:\n')
print(q_table)
5 Sarsa
参考文献
Q-learning优点是:因为它对完成任务渴望,所以更容易完成任务;缺点是:因为缺乏探索开拓精神,所以完成任务的动作比较单一,造成任务完成时动作不一定是最潇洒的。
Sarsa优点是:因为它有探索开拓精神,所以有概率探索出最潇洒的完成动作;缺点是:由于完成任务的饥渴程度可以手动调节,所以Sarsa并不一定那么热衷于完成任务。
Sarsa-lambda优点是:由于多了一张eligibility_trace表,那么就有了探索轨迹的记录,且此轨迹对Q_TABLE的数据产生正面或负面的影响,所以Sarsa-lambda比Sarsa能更快的学会完成任务;缺点是:由于学的快,却不一定学的精,且特容易思维僵化,总爱用固定的动作完成任务,哪怕这个动作并不潇洒,却愈发坚持,用“固执”来形容都不为过。代码这样写:self.eligibility_trace.ix[s, a] += 1,Sarsa-lambda固执的情绪会愈发的严重,elf.eligibility_trace.ix[s, :] *= 0; self.eligibility_trace.ix[s, a] = 1这样写可以缓解Sarsa-lambda固执情绪的积累速度,要好一些。
6 最大熵
首先,我们先介绍下什么是最大熵。对于这个概念的理解,推荐大家读一读吴军老师的《数学之美》第20章。关于最大熵模型的公式推导,建议大家读一读李航老师的《统计学习方法》第6章。在概率论中,熵是不确定性的度量。不确定性越大,熵越大。比如,在区间固定时,所有的分布中均匀分布的熵最大。因为均匀分布在固定区间每一点取值的概率都相等,所以取哪个值的不确定性最大。最大熵原理是指,在学习概率模型时,在所有满足约束的概率模型(分布)中,熵最大的模型是最好的模型。这是因为,通过熵最大所选取的模型,没有对未知(即除了约束已知外)做任何主观假设。也就是说,除了约束条件外,我们不知道任何其他信息。比如当我们猜测一个筛子每个面朝上的概率是多少时,我们猜每个面朝上的概率都是1/6,其实这个解就是最大熵解。因为,我们除了知道每个面朝上的概率加起来等于1外,其他条件都是不知道的,这时猜测出的均匀分布就是最大熵解。
作者:天津包子馅儿
链接:https://zhuanlan.zhihu.com/p/26855870
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
Policy-based
policy-based实战
-
mean squared error: 各数据偏离真实值的距离的平方和 的平均数

1 M N ∑ i = 1 M ∑ j = 1 N ( x j , k − x j , k ′ ) 2 \frac{1}{MN} \sum_{i=1}^M \sum_{j=1}^N \left( x_{j,k} - x'_{j,k} \right ) ^ {2} MN1i=1∑Mj=1∑N(xj,k−xj,k′)2 -
数据中心化和标准化
参考文献
return out / np.std(out - np.mean(out))
- log likelihoods
因为涉及到的估计函数往往是是指数型族,取对数后不影响它的单调性但会让计算过程变得简单,所以就采用了似然函数的对数,称“对数似然函数