matlab三次样条曲线的绘制（spline和csape函数详解）
matlab三次样条函数的绘制（spline和csape函数详解）
样条函数是工程中常用的插值函数。早期工程师制图时，把富有弹性的细长木条（所谓样条）用压铁固定在样点上，在其他地方让它自由弯曲，然后沿木条画下曲线。对于样条本身，可以利用材料力学的大柔度梁理论建立梁的挠度方程，根据理论，样条可以用分段插值三次函数表示。
由于样条曲线具有连续的二阶导数，所以光滑性好。matlab里有两个函数可以绘制样条曲线，一个是spline，一个是csape。虽然interp1中也可以绘制，优点是代码简单而且可以方便更换其它插值方法，但是功能也比较简单，对于边界条件的无法设置。
关于interp1可以参见官方帮助https://ww2.mathworks.cn/help/matlab/ref/interp1.html
三次样条曲线有4种边界条件。
- 自然边界条件，二阶导数在边界处为0，可视为简支梁，是最常用的边界条件。
- 第一边界条件，二阶导在边界处已知的边界条件。自然边界条件可视为特例。
- 第二边界条件，一阶导在边界处已知的边界条件。
- 循环边界条件，一阶导与二阶导在边界处相等的边界条件，适用于封闭或循环的图形。
如果既有第一边界由于第二边界，称为混合边界条件。
1.spline函数详解
spline函数只能实现自然边界条件和第二边界条件，可以实现一维或者高维的曲线插值。
官方spline实例可以参见：https://ww2.mathworks.cn/help/matlab/ref/spline.html
1.一维自然边界条件
格式cs=spline(x,y);
输入：x自变量，y函数值
输出：cs为三维样条插值函数构建的结构体。
cs结构体调用方法为yy=ppval(cs,xx);
xx为插值点，yy为插值得到的函数值。
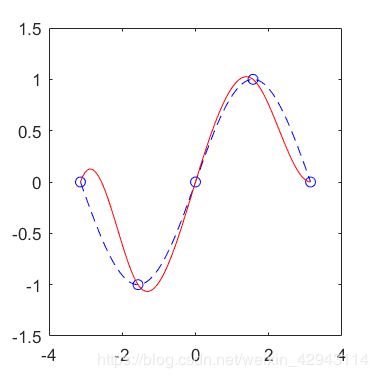
%正弦曲线
r=pi*linspace(-1,1,100);
yr=sin(xr);
%1自然边界条件
x = pi*linspace(-1,1,5);%设置5个控制点
y = sin(x);
cs = spline(x,y);%样条函数
xx = linspace(x(1),x(end),100);%插值点
yy=ppval(cs,xx);%插值
figure(1)
plot(x,y,'bo',xr,yr,'b--',xx,yy,'r-');%绘图
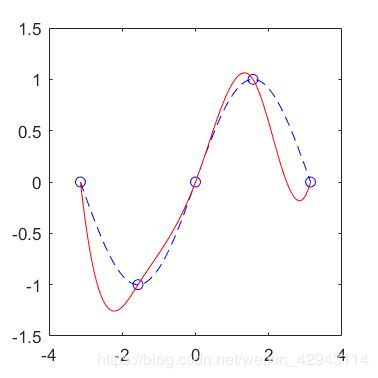
这里自然条件下，y’’(-pi)=y’’(pi)=0。红线为插值函数，蓝线为实际正弦函数。
2.第二边界条件
曲线依然选用上面的曲线，我们使用第二边界条件。
这里依然用上一个xr和yr正弦曲线。y’(-pi)=1，y’(pi)=0。
第二边界条件（导数条件）格式为：
cs=spline(x , [y’1, y, y’2]);
当y比x的长度多2个时，把第一个值和最后一个值当做函数边界的导数。
比如下面代码中，这里x有5个值，y在spline函数中在第一和最后分别增加了1个值作为导数值，第一个值为1，对应y’(-pi)=1；最后一个值为0，对应y’(pi)=0。
%2第二种边界条件，导数确定的
cs2 = spline(x,[1,y,0]);
xx = linspace(x(1),x(end),100);
yy=ppval(cs2,xx);
figure(2)
plot(x,y,'bo',xr,yr,'b--',xx,yy,'r-');
可以看到插值函数被大大改变。
如果想要验证y’(-pi)=1，取(yy(2)-yy(1))/(xx(2)-xx(1))，得0.87（这里不是1的原因是xx太稀疏，xx间隔取越密，越接近1）。
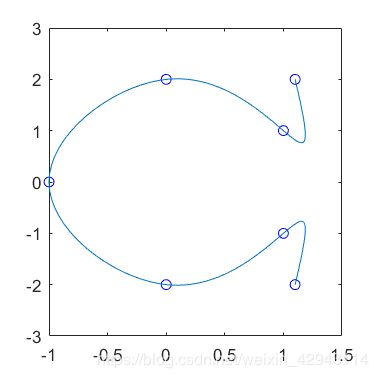
3.高维无约束
这里以二维为例。这里选用两端无约束的自然边界条件。
二维格式为:
cs=spline(t,XY);
输入t为一个正向序列，需要单调。
输入XY为2行n列的矩阵，第一行为x，第二行为y。
cs依然是输出的结构体，但是后面利用ppval插值时要代入关于t的序列值。
XY=[1.1,1,0,-1,0,1,1.1;
2,1,2,0,-2,-1,-2];
t=1:length(XY);%输入XY和t
cs3=spline(t,XY);%样条函数
yy=ppval(cs3,linspace(t(1),t(end),101));%插值
figure(3)
plot(XY(1,:),XY(2,:),'bo',yy(1,:),yy(2,:))
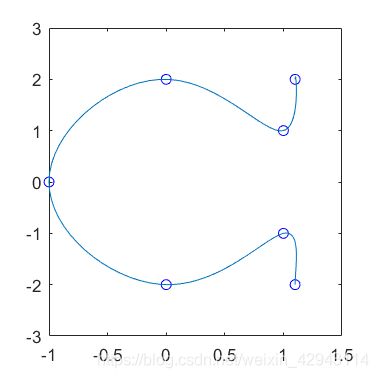
4.高维第二边界
由于1维不能表述当y’(x)=inf的情况（如果输入inf时函数会报错），所以可以利用二维来实现导数为无穷大时的约束。
对于二维情况，导数的表达用向量的形式代替，比如k=1可以表示为（0.707,0.707），k=∞可以用(0,1)表示。
表达格式为
cs=spline(t , [xy’1, xy, xy’2]);
t为序列
xy为坐标，xy’1为第一个点的导数列向量，xy’2为最后一个点的导数列向量
这里第一个点和最后一个点都取负无穷（0 ; -1）
%4高维有斜率约束
%这里用3的t和XY
cs4=spline(t,[[0;-1],XY,[0;-1]]);
yy=ppval(cs4,linspace(t(1),t(end),101));
figure(4)
plot(XY(1,:),XY(2,:),'bo',yy(1,:),yy(2,:))
可以看到有负无穷约束的条件下，改善了图形向外弯折。
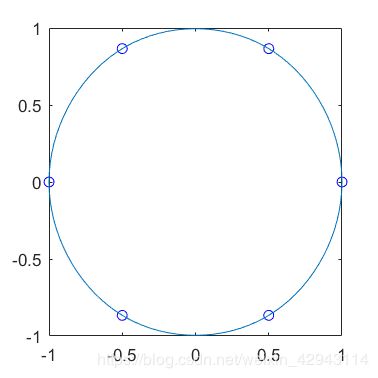
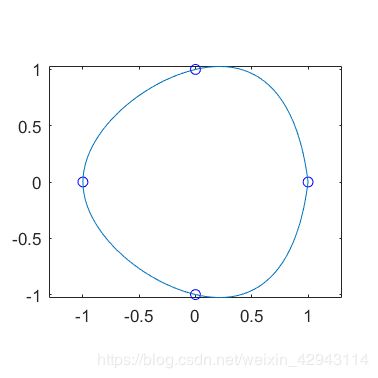
5.利用第二边界条件绘制圆
虽然圆是一个封闭图形，需要用到循环边界条件，但是如果我们已知圆一点处的导数，还是可以间接的利用这点的导数去做一个伪循环条件的。
比如在（1,0）点处作为初始点，逆时针一圈回到（1,0）点。两边一阶导均为正无穷。算法实现如下：
%5圆形绘制
t = pi*linspace(0,2,7);
XY=[cos(t);sin(t)];
cs5=spline(t,[[0;1],XY,[0;1]]);
yy=ppval(cs5,linspace(t(1),t(end),101));
figure(5)
plot(XY(1,:),XY(2,:),'bo',yy(1,:),yy(2,:))
2.csape函数详解
csape函数可以实现三次样条曲线的各种条件，包括第一边界、第二边界、循环边界、混合边界等。可以实现一维至多维的各种情况。
1.自然边界条件
调用格式同spline函数，这里就不展开了。
cs =csape(x,y)
2。第一边界条件
调用格式：
cs = csape(x , [y’‘1 , y , y’‘2] , [2 , 2] )
其中x、y和y’'1(2)和之前定义都一样，是约束值，只是这个函数多了一项。
第三项，即[2,2]代表第一个值和最后一个值，都是样条函数的2阶导数值约束条件。
举例为
%采用cs1的x和y值，即正弦曲线值
cs6 = csape(x,[5,y,5],[2,2]);%样条插值
xx = linspace(x(1),x(end),100);
yy=ppval(cs6,xx);
figure(6)
plot(x,y,'bo',xr,yr,'b--',xx,yy,'r-');
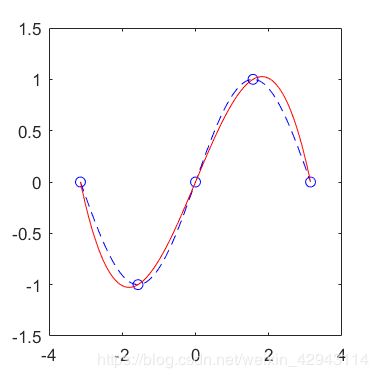
3.第二边界条件&混合边界条件
这里第三项取[1,1]即为第二边界条件，即1阶导数约束点。
如果取[1,2]或[2,1]即为混合边界条件。
这里仅用第二边界举例
cs7 = csape(x,[-1,y,-1],[1,1]);
xx = linspace(x(1),x(end),100);
yy=ppval(cs7,xx);
figure(7)
plot(x,y,'bo',xr,yr,'b--',xx,yy,'r-');
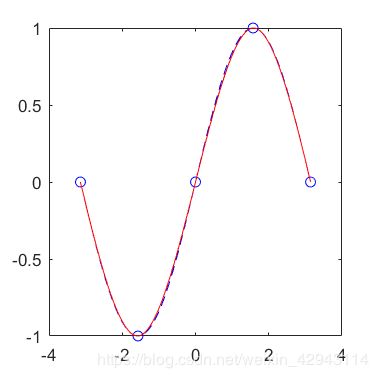
可以看到和之前用二阶导等于0约束相比，用一阶导都等于-1的精度要更高。
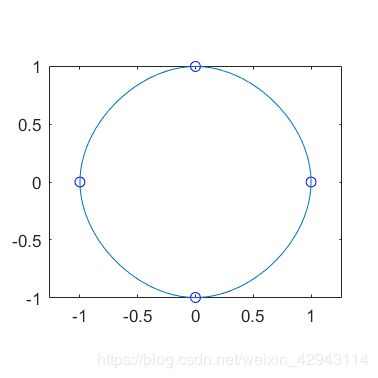
4.二维循环边界条件
这里csape函数高维的调用格式依然同spline，具体参见前面的例子。
这里第三项为[0,0]时，代表循环边界条件，不仅适用于1维，还适用于更高维。
比如还是那绘制圆形举例：
%9二维自然条件
t = pi*linspace(0,2,5);
XY=[cos(t);sin(t)];
cs9=csape(t,XY);
yy=ppval(cs9,linspace(t(1),t(end),101));
figure(9)
plot(XY(1,:),XY(2,:),'bo',yy(1,:),yy(2,:))
axis equal
%10二维循环
cs10=csape(t,XY,[0,0]);%只多了第三项
yy=ppval(cs10,linspace(t(1),t(end),101));
figure(10)
plot(XY(1,:),XY(2,:),'bo',yy(1,:),yy(2,:))
在(1,0)点自然无约束条件↑↑↑。
在(1,0)点循环约束↑↑↑。