MATLAB强化学习入门——三、深度Q学习与神经网络工具箱

零、为什么需要深度Q学习

上一期的文章《网格迷宫、Q-learning算法、Sarsa算法》的末尾，我们提到了Q学习固有的缺陷：由于智能体(agent)依赖以状态-动作对为自变量的Q函数表(Q Function Table)来形成对当前状态的估计，并以此为依据利用策略π选择动作。Q函数表就必须包含智能体在环境中所可能出现的所有动作-状态对及其对应Q值。显然，当一个多步决策问题变得足够复杂甚至变为连续决策或控制问题时，Q学习本身是无力应对的。例如，对于复杂的多步决策问题，庞大而结构复杂的Q表将变得难以存储和读取；将网格迷宫的长、宽各扩大10倍，Q表则变成原来的100倍。对于连续决策/控制问题时，Q表更是无法记录所有的状态。
那么，如何解决这一问题呢？
一个直截的想法就是，选择某个多元函数，逼近Q表中“自变量”动作-状态对与“因变量”Q值形成的关系。但这样做依然存在问题：对于不同的强化学习问题，Q表中的数据呈现出各异的曲线特性，只有找到符合Q表数据的函数形式，才可能良好的逼近Q表。选择传统函数进行逼近，显然是很难实现编程自动化的。
神经网络(Neural Network)恰恰是这么一种有别于传统函数逼近的解决方案。而从数学的角度讲，神经网络本质上就是一种强大的非线性函数逼近器。将神经网络与Q学习结合起来，就得到了能够解决更复杂问题的Q-Network以及使用深度神经网络的Deep-Q-Network (DQN)。
Deep-Q-Learning的算法究竟是什么样的？浙江大学的《机器学习和人工智能》MOOC有着大致的讲解。而如何实现Deep-Q-Learning？莫烦Python以及北理工的MOOC也给出了Python语言的详细示范。
尽管有关Deep-Q-Learning的程序和讲解已经很多权威且易懂的内容；准确的理解Deep-Q-Learning算法，并在MatLab上实现，则是完成强化学习控制这个最终目标的关键。具体到Deep-Q-Learning的实现上，它不仅与之前的Q-Learning在程序结构上有着相当大的区别，直接将它应用于连续控制问题也会是非常跳跃的一步。因此，在这一期的文章里，问题将聚焦在前后两个问题之间：如何使用神经网络让智能体走好网格迷宫？
将这个问题再细分开来，则包括两部分：

1. 如何使用MatLab的神经网络工具箱？
2. 如何实现深度Q学习算法？

第三期主要包含两部分内容，第一部分即上文，简要介绍了深度Q学习的存在基础，另一部分则解决第一个小问题，讨论一下MatLab神经网络工具箱的使用。在第四期，我们再详细聊一聊深度Q学习在网格迷宫中的实现。

一、神经网络工具箱(Neural Network Toolbox)

MatLab自版本R2006a就开始提供自定义构建神经网络模型的函数；到目前为止，除机器学习方向科研人员外，Matlab的神经网络工具箱已经能满足其余使用者对神经网络模型的绝大部分需求。用户除去可以使用feedforwardnet()函数构建定制的全连接前馈神经网络外， 还可以直接调用封装好的经典卷积神经网络(convolutional neural network)模型ALEXnet、VGG16、Googlenet等。
本文不打算详细介绍或讨论关于神经网络方面的理论知识，作者本人自忖也没有综论这方面知识的能力和水平。如果想要进一步了解这方面知识的，可以移步浙江大学《机器学习和人工智能》MOOC以及周志华教授的西瓜书。尽管如此，一些概念还是需要在此阐明一下，以方便之后Deep-Q-Network的实现。

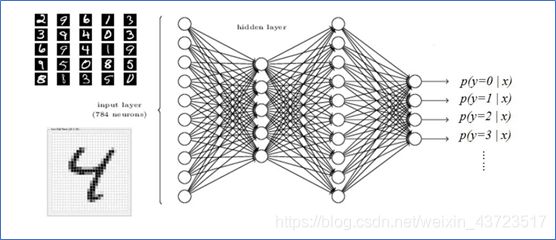
图1 神经网络模型

简言之，神经网络结构有多层的神经元单元及相互之间的连接构成。对于全连接神经网络，任意一层A的任意一个神经元a_1都存在与下一层B的所有神经元b_i的连接，A层内的神经元则不相互连接；换句话说，B层的任意一个神经元b_1的输入为上一层所有神经元输出的加权总和。假设A层有m个神经元，B层有n个，则B层第j个神经元的输入为：

其中w_ij为神经元对的连接权重。如上式所表示的，不同的权重反映了两神经元之间联系的紧密程度。在B层的神经元内部，则将输入IN_bj通过例如Sigmoid和Relu等函数将输入进行非线性变换得到输出，再传输至下一层。通过如上的传递方式，前馈神经网络将输入从第一层映射至最后层获得输出，这一结果即为神经网络的预测输出。
对于一个未训练的神经网络，预测输出显然不会与实际期望结果相等。也因此，我们需要标注了正确结果的数据训练神经网络，使它能够真正拟合数据集输入与输出间的映射关系。而这一训练方式，我们称为反向传播(backpropagation)。最基础的反向传播训练方法为梯度下降法(gradient descent)，以此为基础，为提高反向传播训练的收敛速度，又提出了带动量的梯度下降法(gradient descent with momentum)等训练方法；另外，在MatLab中，还提供包括Levenberg-Marquardt方法等的反向传播算法。
考虑具体的网格迷宫问题以及姿态控制问题，适用于图像识别的卷积神经网络(CNN)并不是我们所需要的。普通的前馈神经网络模型即以足够，MatLab除去可以使用feedforwardnet()函数构建前馈神经网络外，还提供了函数拟合网络fitnet()、模式识别网络patternnet()两种特殊的前馈神经网络。
对于网格迷宫问题，我们希望神经网络模型能够在以状态-动作对为输入的情况下输出对应Q值。因此，可以调用fitnet()函数去拟合从状态-动作对至Q函数值的映射关系。

二、fitnet()的调用与训练

作为前馈神经网络的一种特殊形式，fitnet()本质上与feedforwardnet()没有太大差别。从MatLab语言上来说，两者的调用、训练、计算以及参数的调整也都是一致的。
MatLab神经网络工具箱对用户非常友好，可以直接使用一行代码完成前馈神经网络的结构初始化：

%%构建指定层数及神经元数目的fitnet
QNet=fitnet([10,10,5]);     %行向量的元素数为神经网络隐层的数目，每一个元素对应该层的神经元个数

同样，构建好符合格式要求的训练数据集后，MatLab也提供集成化的训练函数train()进行神经网络的训练：

QNet=train(QNet,TrainsSet,TargetSet);

完成神经网络的训练后，我们即可以使用该神经网络预测结果了：

Output=QNet(Input);

在训练神经网络和调用神经网络进行计算时，MatLab提供了使用GPU进行计算的选项：

QNet=train(QNet,TrainsSet,TargetSet,’useGPU’,’yes’);
Output=QNet(Input,’useGPU’,’yes’);

对于普通个人电脑，直接调用GPU进行神经网络运算的速度并不如使用CPU运算。因此，在之后的DQN实现中，我们也不会调用GPU进行运算。

另一个随后要用到的，是神经网络模型中一系列有关训练的参数设置。MatLab中，train()函数本身并不定义反向传播和迭代收敛的任何参数，而将这些参数保存在神经网络对象中。在训练过程中，train()函数访问神经网络对象中保存的训练参数对神经网络进行训练。这样，对于几乎所有神经网络，用户都能在不主动调整train()参数情况下有针对性地对神经网络进行训练。fitnet()函数默认的反向传播训练算法为Levenberg-Marquardt方法；而DQN所需要的训练算法则为梯度下降法，可以用如下的方式进行修改。而其它训练参数的调用与修改也是类似的。

QNet.trainFcn=’traingdx’  %修改为自适应动量梯度下降法

三、练习：拟合二维曲面

具体的来说，我们用一个拟合二维曲面的问题来熟悉神经网络这一对象的使用：

clear all;

%%构建指定层数及神经元数目的fitnet
QNet=fitnet([10,10,5]);     %行向量的元素数为神经网络隐层的数目，每一个元素对应该层的神经元个数
%神经网络初始化后，内部参数尚处于没有训练的过程，输入层和输出层元素的个数也没有定义，可以通过训练进行定义

%%训练神经网络
%使用标记好的数据集对QNet进行训练。假设有k个样本，神经网络的输入变量为m个，输出变量为n个，则输入数据的格式为m行*k列的矩阵，输出数据为n行*k列的矩阵。
%我们在测试该网络时，假设它有两个自变量输入以及一个输出，因此如下生成训练数据集。
%假设目标函数为如下形式：
[X1,Y1]=meshgrid(0.1:0.1:3,0.2:0.2:6);    %绘图用横纵坐标
target1=sin(1.5*sqrt(X1)+1*Y1);
x=0.1:0.1:3;
y=0.2:0.2:6;
%将上述结构转换成符合神经网络输入、输出的格式
Dataset=zeros(3,900);
for i=1:30
    for j=1:30
        Dataset(1,(i-1)*30+j)=x(i);
        Dataset(2,(i-1)*30+j)=y(j);
        Dataset(3,(i-1)*30+j)=target1(i,j);
    end
end
%抽取其中部分数据得到训练数据集1
num1=200;
Trainset11=zeros(3,num1);
for i=1:num1
    Trainset11(:,i)=Dataset(:,unidrnd(900));
end
%训练神经网络
QNet=train(QNet,Trainset11(1:2,:),Trainset11(3,:));

%%使用神经网络预测结果
%获得训练好的神经网络后，我们即可以用该神经网络根据输入预测输出
Input=Dataset(1:2,:);  %生成与目标数据集相同的输入数据
Output1=QNet(Input);
Surf1=zeros(30,30);
for i=1:30
    for j=1:30
        Surf1(i,j)=Output1((i-1)*30+j);
    end
end
%%绘图对比结果
%我们将神经网络的预测输出和实际函数值采用surf()函数进行可视化的对比
%彩色表面图为真实输出
surf(X1,Y1,target1,'FaceAlpha',0.5);
hold on;
%绿色表面图为预测输出
CO(:,:,1) = zeros(30); % red
CO(:,:,2) = ones(30).*linspace(0.2,0.8,30); % green
CO(:,:,3) = zeros(30); % blue
surf(X1,Y1,Surf1,CO,'FaceAlpha',0.7);

四、神经网络的调用效率问题

在熟悉了神经网络对象的一些基本使用方法后，我们最后来聊一聊神经网络的调用效率问题。在传统的Q学习中，我们需要在智能体进行一步学习时两次Q表以获得当前状态-动作对以及下一状态-动作对的Q值。将这一方法不变的迁移到神经网络模型中，也就是说我们需要调用QNet()分别对两组单独的数据进行计算，在MatLab中，这样的计算效率是非常低的。在上文训练完成的神经网络下，我们用下面的方式进行对比：

%代码1
num2=400;
Input1=Dataset(1:2,1:num2);
Output1=QNet(Input1);

%代码2
num2=400;
Input1=Dataset(1:2,1:num2);
Output1=zeros(1,num2);
for i=1:num2
    Output1(i)=QNet(Input(:,i));
End

使用运行并计时功能对比两段代码的用时：

显然，这两段代码实现了相同的功能，然而耗时却明显不同。代码1用时约0.2s，代码2用时却超过4s。这是因为MatLab神经网络对象中的内置函数net.Hints()及net.subserf()等函数的单次调用耗时较长的原因。
也因此，在之后的编程中，为了提高程序的整体效率，高效调用神经网络是必须要考虑的重点。

以上就是第三期我们要讨论的全部内容，由于这一期并不涉及结构复杂的代码，所以全部代码均在文章中呈现。

十分欢迎各位读者讨论和打赏~