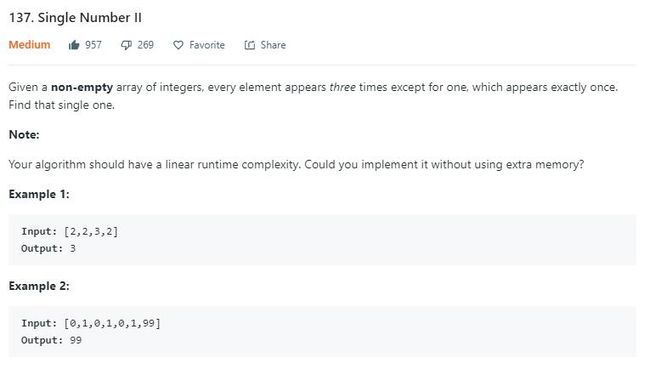
LeetCode 力扣 137. 只出现一次的数字 II

题目描述（中等难度）

136 题 的升级版，这个题的话意思是，每个数字都出现了 3 次，只有一个数字出现了 1 次，找出这个数字。同样要求时间复杂度为 O（n），空间复杂度为 O（1）。

大家可以先看一下 136 题 ，完全按 136 题 的每个解法去考虑一下。

解法一

先不考虑空间复杂度，用最常规的方法。

可以用一个 HashMap 对每个数字进行计数，然后返回数量为 1 的数字就可以了。

public int singleNumber(int[] nums) {
    HashMap<Integer, Integer> map = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        if (map.containsKey(nums[i])) {
            map.put(nums[i], map.get(nums[i]) + 1);
        } else {
            map.put(nums[i], 1);
        }
    }
    for (Integer key : map.keySet()) { 
        if (map.get(key) == 1) {
            return key;
        }

    }
    return -1; // 这句不会执行
}

时间复杂度：O（n）。

空间复杂度：O（n）。

解法二 数学推导

回想一下 136 题 中，每个数字都出现两次，只有一个数字出现 1 次是怎么做的。

假设我们的数字是 a b a b c c d

怎么求出 d 呢？

只需要把出现过的数字加起来乘以 2 ，然后减去之前的数字和就可以了。

什么意思呢？

上边的例子出现过的数字就是 a b c d ，加起来乘以二就是 2 * ( a + b + c + d)，之前的数字和就是 a + b + a + b + c + c + d 。

2 * ( a + b + c + d) - (a + b + a + b + c + c + d)，然后结果是不是就是 d 了。。。。。。

看完这个解法我只能说 tql。。。

找出现过什么数字，我们只需要一个 Set 去重就可以了。

这里的话每个数字出现了 3 次，所以我们可以加起来乘以 3 然后减去之前所有的数字和。这样得到的差就是只出现过一次的那个数字的 2 倍。

public int singleNumber(int[] nums) {
    HashSet<Integer> set = new HashSet<>();
    int sum = 0;
    for (int i = 0; i < nums.length; i++) {
        set.add(nums[i]);
        sum += nums[i];
    }
    int sumMul = 0;
    for (int n : set) {
        sumMul += n;
    }
    sumMul = sumMul * 3;
    return (sumMul - sum) / 2;
}

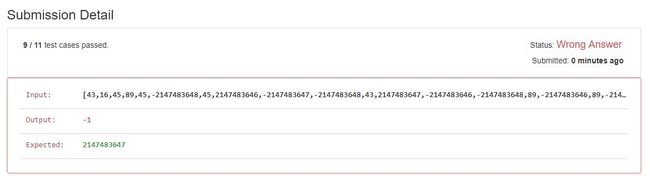
然而并没有通过

原因就是 int 是 32 位整数，计算机中是以补码表示的，详细的参考 趣谈补码 。
问题的根本就出现在，如果 2a = c ，那么对于 a 的取值有两种情况。在没有溢出的情况下，a = c/2 是没有问题的。但如果 a 是很大的数，加起来溢出了，此时 a = c >>> 1。

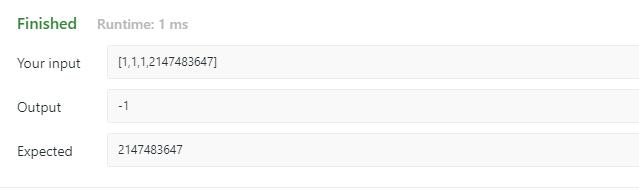
举个具体的例子，

如果给定的数组是 [1 1 1 Integer.MaxValue]。如果按上边的解法最后得到的就是

(1 + Ingeger.MaxValue) * 3 - (1 + 1 + 1 + Integer.MaxValue) = 2 * Integer.MaxValue

由于产生了溢出

2 * Integer.MaxValue = -2，最后我们返回的结果就是 -2 / 2 = -1。

所以这个思路行不通了，因为无法知道是不是会溢出。

解法三 位操作

136 题通过异或解决了问题，这道题明显不能用异或了，参考 这里 的一个解法。

我们把数字放眼到二进制形式

假如例子是 1 2 6 1 1 2 2 3 3 3, 3 个 1, 3 个 2, 3 个 3,1 个 6
1 0 0 1
2 0 1 0 
6 1 1 0 
1 0 0 1
1 0 0 1
2 0 1 0
2 0 1 0
3 0 1 1  
3 0 1 1
3 0 1 1      
看最右边的一列 1001100111 有 6 个 1
再往前看一列 0110011111 有 7 个 1
再往前看一列 0010000 有 1 个 1
我们只需要把是 3 的倍数的对应列写 0，不是 3 的倍数的对应列写 1    
也就是 1 1 0,也就是 6。

原因的话，其实很容易想明白。如果所有数字都出现了 3 次，那么每一列的 1 的个数就一定是 3 的倍数。之所以有的列不是 3 的倍数，就是因为只出现了 1 次的数贡献出了 1。所以所有不是 3 的倍数的列写 1，其他列写 0 ，就找到了这个出现 1 次的数。

public int singleNumber(int[] nums) {
    int ans = 0;
    //考虑每一位
    for (int i = 0; i < 32; i++) {
        int count = 0;
        //考虑每一个数
        for (int j = 0; j < nums.length; j++) {
            //当前位是否是 1
            if ((nums[j] >>> i & 1) == 1) {
                count++;
            }
        }
        //1 的个数是否是 3 的倍数
        if (count % 3 != 0) {
            ans = ans | 1 << i;
        }
    }
    return ans;
}

时间复杂度：O（n）。

空间复杂度：O（1）。

解法四 通用方法

参考 这里。

解法三中，我们将数字转为二进制，统计了每一位的 1 的个数。我们使用了一个 32位 的 int 来统计。事实上，我们只需要看它是不是 3 的倍数，所以我们只需要两个 bit 位就够了。初始化为 00，遇到第一个 1 变为 01，遇到第二个 1 变为 10，遇到第三个 1 变回 00 。接下来就需要考虑怎么做到。

本来想按自己理解的思路写一遍，但 这里 写的很好了，主要还是翻译下吧。

将问题一般化

给一个数组，每个元素都出现 k ( k > 1) 次，除了一个数字只出现 p 次(p >= 1, p % k !=0)，找到出现 p 次的那个数。

考虑其中的一个 bit

为了计数 k 次，我们必须要 m 个比特，其中 $2^m>=k$ ，也就是 m >= logk。

假设我们 m 个比特依次是 $x_m{x}_{m-1}...x_2{x}_1$ 。

开始全部初始化为 0。00...00。

然后扫描所有数字的当前 bit 位，用 i 表示当前的 bit。

也就是解法三的例子中的某一列。

假如例子是 1 2 6 1 1 2 2 3 3 3, 3 个 1, 3 个 2, 3 个 3,1 个 6
1 0 0 1
2 0 1 0 
6 1 1 0 
1 0 0 1
1 0 0 1
2 0 1 0
2 0 1 0
3 0 1 1  
3 0 1 1
3 0 1 1   

初始 状态 00...00。

第一次遇到 1 , m 个比特依次是 00...01。

第二次遇到 1 , m 个比特依次是 00...10。

第三次遇到 1 , m 个比特依次是 00...11。

第四次遇到 1 , m 个比特依次是 00..100。

x1 的变化规律就是遇到 1 变成 1 ，再遇到 1 变回 0。遇到 0 的话就不变。

所以 x1 = x1 ^ i，可以用异或来求出 x1 。

那么 x2...xm 怎么办呢？

x2 的话，当遇到 1 的时候，如果之前 x1 是 0，x2 就不变。如果之前 x1 是 1，对应于上边的第二次遇到 1 和第四次遇到 1。 x2 从 0 变成 1 和 从 1 变成 0。

所以 x2 的变化规律就是遇到 1 同时 x1 是 1 就变成 1，再遇到 1 同时 x1 是 1 就变回 0。遇到 0 的话就不变。和 x1 的变化规律很像，所以同样可以使用异或。

x2 = x2 ^ (i & x1)，多判断了 x1 是不是 1。

x3，x4 ... xm 就是同理了，xm = xm ^ (xm-1 & ... & x1 & i) 。

再说直接点，上边其实就是模拟了每次加 1 的时候，各个比特位的变化。所以高位 xm 只有当低位全部为 1 的时候才会得到进位 1 。

00 -> 01 -> 10 -> 11 -> 00

上边有个问题，假设我们的 k = 3，那么我们应该在 10 之后就变成 00，而不是到 11。

所以我们需要一个 mask ，当没有到达 k 的时候和 mask进行与操作是它本身，当到达 k 的时候和 mask 相与就回到 00...000。

根据上边的要求构造 mask，假设 k 写成二进制以后是 km...k2k1。

mask = ~(y1 & y2 & ... & ym),

如果kj = 1，那么yj = xj

如果 kj = 0，yj = ~xj 。

举两个例子。

k = 3: 写成二进制，k1 = 1, k2 = 1, mask = ~(x1 & x2);

k = 5: 写成二进制，k1 = 1, k2 = 0, k3 = 1, mask = ~(x1 & ~x2 & x3);

很容易想明白，当 x1x2...xm 达到 k1k2...km 的时候因为我们要把 x1x2...xm 归零。我们只需要用 0 和每一位进行与操作就回到了 0。

所以我们只需要把等于 0 的比特位取反，然后再和其他所有位相与就得到 1 ，然后再取反就是 0 了。

如果 x1x2...xm 没有达到 k1k2...km ，那么求出来的结果一定是 1，这样和原来的 bit 位进行与操作的话就保持了原来的数。

总之，最后我们的代码就是下边的框架。

for (int i : nums) {
    xm ^= (xm-1 & ... & x1 & i);
    xm-1 ^= (xm-2 & ... & x1 & i);
    .....
    x1 ^= i;
    
    mask = ~(y1 & y2 & ... & ym) where yj = xj if kj = 1, and yj = ~xj if kj = 0 (j = 1 to m).

    xm &= mask;
    ......
    x1 &= mask;
}

考虑全部 bit

假如例子是 1 2 6 1 1 2 2 3 3 3, 3 个 1, 3 个 2, 3 个 3,1 个 6
1 0 0 1
2 0 1 0 
6 1 1 0 
1 0 0 1
1 0 0 1
2 0 1 0
2 0 1 0
3 0 1 1  
3 0 1 1
3 0 1 1   

之前是完成了一个 bit 位，也就是每一列的操作。因为我们给的数是 int 类型，所以有 32 位。所以我们需要对每一位都进行计数。有了上边的分析，我们不需要再向解法三那样依次考虑每一位，我们可以同时对 32 位进行计数。

对于 k 等于 3 ，也就是这道题。我们可以用两个 int，x1 和 x2。x1 表示对于 32 位每一位计数的低位，x2 表示对于 32 位每一位计数的高位。通过之前的公式，我们利用位操作就可以同时完成计数了。

int x1 = 0, x2 = 0, mask = 0;

for (int i : nums) {
    x2 ^= x1 & i;
    x1 ^= i;
    mask = ~(x1 & x2);
    x2 &= mask;
    x1 &= mask;
}

返回什么

最后一个问题，我们需要返回什么？

解法三中，我们看 1 出现的个数是不是 3 的倍数，不是 3 的倍数就将对应位置 1。

这里的话一样的道理，因为所有的数字都出现了 k 次，只有一个数字出现了 p 次。

因为 xm...x2x1 组合起来就是对于每一列 1 的计数。举个例子

假如例子是 1 2 6 1 1 2 2 3 3 3, 3 个 1, 3 个 2, 3 个 3,1 个 6
1 0 0 1
2 0 1 0 
6 1 1 0 
1 0 0 1
1 0 0 1
2 0 1 0
2 0 1 0
3 0 1 1  
3 0 1 1
3 0 1 1   
    
看最右边的一列 1001100111 有 6 个 1, 也就是 110
再往前看一列 0110011111 有 7 个 1, 也就是 111
再往前看一列 0010000 有 1 个 1, 也就是 001
再对应到 x1, x2, x3 就是
x1 1 1 0
x2 0 1 1
x3 0 1 1

如果 p = 1，那么如果出现一次的数字的某一位是 1 ，一定会使得 x1 ，也就是计数的最低位置的对应位为 1，所以我们把 x1 返回即可。对于上边的例子，就是 110 ，所以返回 6。

如果 p = 2，二进制就是 10，那么如果出现 2次的数字的某一位是 1 ，一定会使得 x2 的对应位变为 1，所以我们把 x2 返回即可。

如果 p = 3，二进制就是 11，那么如果出现 3次的数字的某一位是 1 ，一定会使得 x1 和x2的对应位都变为1，所以我们把 x1 或者 x2 返回即可。

所以这道题的代码就出来了

public int singleNumber(int[] nums) {
    int x1 = 0, x2 = 0, mask = 0;
    for (int i : nums) {
        x2 ^= x1 & i;
        x1 ^= i;
        mask = ~(x1 & x2);
        x2 &= mask;
        x1 &= mask;
    }
    return x1; 
}

至于为什么先对 x2 异或再对 x1 异或，就是因为 x2 的变化依赖于 x1 之前的状态。颠倒过来明显就不对了。

再扩展一下题目，对于 k = 5, p = 3 怎么做，也就是每个数字出现了5 次，只有一个数字出现了 3 次。

首先根据 k = 5，所以我们至少需要 3 个比特位。因为 2 个比特位最多计数四次。

然后根据 k 的二进制形式是 101，所以 mask = ~(x1 & ~x2 & x3)。

根据 p 的二进制是 011，所以我们最后可以把 x1 返回。

public int singleNumber(int[] nums) {
    int x1 = 0, x2 = 0, x3  = 0, mask = 0;
    for (int i : nums) {
        x3 ^= x2 & x1 & i;
        x2 ^= x1 & i;
        x1 ^= i;
        mask = ~(x1 & ~x2 & x3);
        x3 &= mask;
        x2 &= mask;
        x1 &= mask;
    }
    return x1;  
}

而 136 题 中，k = 2, p = 1 ，其实也是这个类型。只不过因为 k = 2，而我们用一个比特位计数的时候，等于 2 的时候就自动归零了，所以不需要 mask，相对来说就更简单了。

public int singleNumber(int[] nums) {
    int x1 = 0;

    for (int i : nums) {
        x1 ^= i;
    }

    return x1;
}

这个解法真是太强了，完全回到二进制的操作，五体投地了，推荐再看一下英文的 原文 分析，太强了。

总

解法一利用 HashMap 计数很常规，解法二通过数学公式虽然没有通过，但溢出的问题也就我们经常需要考虑的。解法三把数字放眼到二进制，统计 1 的个数已经很强了。解法四直接利用 bit 位来计数，真的是大开眼界了，神仙操作。

更多详细通俗题解详见 leetcode.wang 。