FastGCN： fast learning with graph convolutional networks via importance sampling 论文详解 ICLR 2018

论文题目：FastGCN:fast learning with graph convolutional networks via importance sampling FastGCN:通过重要性采样，利用图卷积网络进行快速学习

作者：来自IBM Research的Jie Chen, Tengfei Ma, Cao Xiao

时间：2018

来源：ICLR

论文链接：https://arxiv.org/pdf/1801.10247.pdf

Github链接：https://github.com/matenure/FastGCN

由Kipf and Welling在2017年提出来的GCN是一个处理半监督学习很有效的图模型。但是，递归的跨层邻域扩展对使用大而密集的图进行训练提出了时间和内存方面的挑战。此文将图卷积解释为概率测度下embedding函数的积分变换。
FastGCN是一种结合了重要性采样的批量训练的算法，不仅可以使GCN的训练更高效，也能很好地泛化到推理中。
实验证明，训练效率提高了几个数量级，而预测仍然相当准确。

1 简单介绍

概率测度 probability measure

概率测度：度量“事件发生的可能性大小”，有相同的概率测度就是指发生的可能性相同，有相同的分布

自助法 bootstrapping

“自助法”（bootstrapping）以自助采样（可重复采样、有放回采样）为基础。

假如一个数据集D有m个样本，看看训练集和测试集怎么选择：

• 训练集D’：每次从数据集D中随机选择一个样本，将这个样本复制一个放到D’中，然后再把原样本放回去（可放回）。重复操作m次。这样D’中就有m个样本了。这种采样方法有可能一个样本会被选择好多次，也有可能有的样本一次也不会被选择到。
• 测试集D-D’：测试集就是那些剩下的，没被选择的样本。

那么训练集D和测试集D’中共有多少数据呢？

可以看出数据集中样本在m次始终不被采样到的概率是$(1-\frac{1}{m}{)}^m$

两个重要的极限公式

$$\underset{m\to 0}{\lim }\frac{\sin m}{m}=1$$
$$\underset{m\to 0}{\lim }{\left(1+x\right)}^{\frac{1}{x}}=e$$
令$m=\frac{1}{t}$，取极限得：

$$\underset{m\to \propto }{\lim }(1-\frac{1}{m}{)}^m=\frac{1}{e}\approx 0.368$$

所以数据集D中有36.8%的样本未出现在训练集中。

优缺点：

• 数据集小、难以划分训练\测试集
• 自助法能从初始数据集中产生多个不同的训练集，可以用于集成学习
• 自助法产生的训练集改变了初始数据集的分布，会引入估计偏差

GCN面临的两个挑战

• GCN是transductive的，但对于实际中的许多应用，测试数据可能不容易获得，因为图形可能随着新的顶点不断扩展（例如，社交网络的新成员、推荐系统的新产品和功能测试的新药物）。这样的场景需要一个inductive的方案，该方案只用一部分训练顶点来学习模型，并且能够很好地推广到有任何扩充的图。

• GCN面临的一个更严峻的挑战是，在批量训练中，跨层递归扩展邻域的代价很大。特别是对于稠密图和幂律图，单顶点邻域的扩展很快占据了图的很大一部分。mini-batch训练即使在batch size很小的时候，也会涉及到和每个batch相关的大量数据。因此，为了使GCN适用于大型、密集的图，可扩展性是一个迫切需要解决的问题。

解决思路（创新点）

• 将图卷积看作是一种概率测度下embedding函数的积分变换
  ，这种方式为inductive学习提供了一个理论支持。具体来说，此文将图的顶点解释为某种概率分布下的独立同分布的样本，并将损失和每个卷积层作为顶点embedding函数的积分。然后，通过定义样本的损失和样本梯度的蒙特卡罗近似计算积分，并且可以进一步改变采样分布（如在重要性采样中）以减小近似方差。

文中提出的FastGCN不仅避免了对测试数据的依赖，还为每个batch的计算产生了可控的代价花费。与GraphSAGE的采样方法相比，FastGCN的采样方案大大减少了梯度的计算（在第3.3节中有更详细的分析）。实验结果表明，FastGCN的每个batch的计算速度比GraphSAGE快一个数量级以上，但分类精度仍然具有很高的可比性。

2 相关工作

为了解决一些基于图结构数据的应用，出现了很多方法。
通过谱图理论产生embedding的方法

• Spectral networks and locally connected networks on graphs. CoRR, abs/1312.6203, 2013
• Deep convolutional networks on graph-structured data. CoRR, abs/1506.05163, 2015
• Convolutional neural networks on graphs with fast localized spectral filtering. CoRR, abs/1606.09375, 2016

通过矩阵分解产生embedding的方法

• Nonlinear dimensionality reduction by locally linear embedding - 2000
• Laplacian eigenmaps and spectral techniques for embedding and clustering - 2001 NIPS
• Distributed large-scale natural graph factorization - 2013
• Learning graph representations with global structural information - 2015 ACM
• Asymmetric transitivity preserving graph embeddin - 2016 ACM SIGKDD

基于随机游走产生embedding的方法

• Deepwalk: Online learning of social representations - 2014 ACM SIGKDD
• Node2vec: Scalable feature learning for networks - 2016 ACM SIGKDD
• Line: Large-scale information network embedding - 2015 WWW
• (SDNE)Structural deep network embedding - 2016 ACM SIGKDD

和此文最相关的方法当属GraphSAGE(Hamilton et al., 2017)，GraphSAGE给出的解决方案相对简单：对一阶邻居进行采样，即采样；充分利用采样后的邻居信息，即聚集。采样的方式简单粗暴，对一阶邻居随机排序；选取固定数量的邻居；少则重复，多则舍弃。对于聚集，GraphSAGE提出了三类聚集器：

• MeanAggregator：element-wisemean。由于采样过程选择为每个节点采样了相同数量的邻居，所以采样后，每个节点度是一样的，所以semi-GCN中的聚集方式（加权求和）可以看作是MeanAggregator的一种特例- PoolingAggregator：element-wise max or mean,包含一层Dense Layer
• LSTMAggregator：训练RNN网络，将邻居特征作为输入

和GraphSAGE的对比

• GraphSAGE作为一种通过聚合邻居节点的信息来生成节点embedding的方式，由于递归地进行邻居扩展，仍然有内存瓶颈的问题
• 为了减少计算开销，GraphSAGE针对每一层限制中间邻居的数量，使用本文的标记，如果在第$l$层对每个顶点采样$t_l$个邻居，那么GraphSAGE扩展的邻居数量在最坏的情况下就是$t_l$个样本的乘积
  FastGCN 和GraphSAGE的区别在于采样的是图中的顶点而不是邻居。涉及到的总的顶点的数量就是$t_l$的和而不是乘积

3 通过采样进行训练和推理

GCN与许多标准神经网络结构的一个显著区别是样本丢失缺乏独立性。基于损失函数对独立数据样本的可加性，目前有SGD（只用一个样本求梯度）及BGD（批量梯度下降，使用所有样本求梯度）等训练算法。针对图上每个顶点都与其所有邻域卷积，此文定义了一个计算效率非常高的样本梯度。

考虑一个使用标准SGD的场景，其中loss是和数据分布$D$相关的一些函数$g$的期望

$$L={\text{E}}_{x\sim D}[g(W;x)]$$
其中，$W$就是模型要优化的参数。
通常，数据分布是不知道的，因此一个作为最小化经验损失的替代做法是把样本$x_1,...,x_n$看作是独立同分布的

$$L_{emp}=\frac{1}{n}\sum _{i=1}^{n}g(W;x),x_i\sim D,{\forall }_i$$
在SGD的每一步中，梯度为$\nabla g(W;x)$。此时，样本的损失和梯度都只涉及一个单独的样本$x_i$。

但是，在图上就不能再利用独立性和通过递归地丢弃样本的邻居节点、邻居节点的邻居节点的信息来计算样本的梯度$\nabla g(W;x)$。

假设一个图$G^{\prime }$，顶点集为$V^{\prime }$，并和一个概率空间$(V^{\prime },F,P)$相关联。在这个概率空间中，可以将$V^{\prime }$看作样本空间，$F$看作事件空间，概率测度$P$定义为一个样本的分布。对于图$G^{\prime }$的子图$G$，它的顶点来源于$V^{\prime }$中根据概率测度计算的独立同分布的样本。

为了解决由于卷积造成的缺乏独立性的问题，文中将网络的每一层解释为顶点的embedding函数（把顶点看作随机变量），这些顶点(随机变量)有相同的概率测度，但彼此独立。

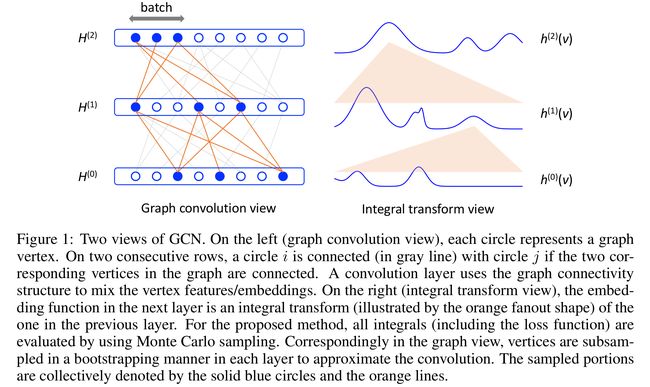
• 图1是GCN的体系结构图
• 左图（图卷积的视角）：每个圆圈代表图中的一个顶点，在连续的两行上，如果图中两个对应的顶点相连，则在网络层中一个圆$i$(用灰色线表示)与圆$j$相连。卷积层使用图形连接结构混合顶点特征/embedding。
• 右图（积分变换的视角）：下一层的embedding函数是前一层的一个积分变换（图中橙色部分所示）。对于此文提出的方法，所有的积分（包括损失函数）都通过蒙特卡罗采样了评估。
• 相应地，在图的视角中，每个层中的顶点都以自助法（bootstrapping）方式进行下采样，以近似卷积。采样部分由蓝色实线和橙色线表示。

GCN的公式如下

$${\tilde{H}}^{(l+1)}=\hat{A}{H}^{(l)}{W}^{(l)},H^{(l+1)}=\sigma \left({\tilde{H}}^{(l+1)}\right),l=0,\dots ,M-1,L=\frac{1}{n}\sum _{i=1}^{n}g\left(H^{(M)}(i,:)\right),\text{\hspace{1em}(1)}$$
用积分变换的形式可以表示为

$${\tilde{h}}^{(l+1)}(v)=\int \hat{A}(v,u)h^{(l)}(u)W^{(l)}dP(u),h^{(l+1)}(v)=\sigma \left({\tilde{h}}^{(l+1)}(v)\right),l=0,\dots ,M-1,\text{\hspace{1em}(2)}$$
损失函数写为
$$L={\mathrm{E}}_{v\sim P}\left[g\left(h^{(M)}(v)\right)\right]=\int g\left(h^{(M)}(v)\right)dP(v),\text{\hspace{1em}(3)}$$

其中

• $u$和$v$是独立的随机变量，它们都有相同的概率测度$P[$
• 函数$h^{(l)}$解释为第$l$层的embedding函数
• 两个连续层的embedding函数通过卷积相互关联，表示为积分变换
• $\hat{A}(u,v)$相当于邻接矩阵$\hat{A}$的$(u,v)$元素
• loss是最后一层的$g(h^{(M)}$对最后的embedding $h^{(M)}$的期望
• 注意，这些积分不是通常的黎曼-斯蒂耶斯（Riemann–Stieltjes）积分，因为变量$u$和$v$是图顶点，而不是实数

以函数形式表示GCN就可以使用蒙特卡罗方法来计算积分，这样就产生了一种批处理的训练算法，也使得训练和测试数据得以分离，就像在归纳学习中一样。

使用$t_l$个独立同分布的样本$u_1^{(l)},\dots ,u_{t_l}^{(l)}\sim P$去近似估计公式（2）中的积分变换，也就是

$${\tilde{h}}_{t_{l+1}}^{(l+1)}(v):=\frac{1}{t_l}\sum _{j=1}^{t_l}\hat{A}\left(v,u_j^{(l)}\right)h_{t_l}^{(l)}\left(u_j^{(l)}\right)W^{(l)},h_{t_{l+1}}^{(l+1)}(v):=\sigma \left({\tilde{h}}_{t_{l+1}}^{(l+1)}(v)\right),l=0,\dots ,M-1$$
其中，约定$h_{t_0}^{(0)}\equiv h^{(0)}$。

然后，公式（3）的loss L容许一个估计量

$$L_{t_0,t_1,\dots ,t_M}:=\frac{1}{t_M}\sum _{i=1}^{t_M}g\left(h_{t_M}^{(M)}\left(u_i^{(M)}\right)\right)$$
结果表明，估计量是一致的（consistent）。这个证明是大数定律和连续映射定理的递归应用；（文中附录部分有介绍）

定理1

如果$g$和$\sigma$是连续的，那么

$$\underset{t_0,t_1,\dots ,t_M\to \infty }{\lim }{L}_{t_0,t_1,\dots ,t_M}=L\text{ with probability one.}$$
在实际应用中，给定一个所有顶点都假定为样本的图。因此，需要使用自助法（bootstrapping）获得一个一致性评估。对于公式（1）的GCN，输出$H^{(M)}$被划分成多个batch。使用$u_1^{(M)},\dots ,u_{t_M}^{(M)}$定义为顶点的一个batch，这些顶点都来自于给定的图。对于每一个batch，采用均匀采样每一层的顶点以获得样本$u_i^{(l)},i=1,\dots ,t_l,l=0,\dots ,M-1$。这种操作等价于对每个$l$的$H^{(l)}$行进行均匀采样。然后，可以获得batch loss

$$L_{\mathrm{b}\mathrm{a}\mathrm{t}\mathrm{c}\mathrm{h}}=\frac{1}{t_M}\sum _{i=1}^{t_M}g\left(H^{(M)}\left(u_i^{(M)},:\right)\right),\text{\hspace{1em}(4)}$$
递归地计算

$$H^{(l+1)}(v,:)=\sigma \left(\frac{n}{t_l}\sum _{j=1}^{t_l}\hat{A}\left(v,u_j^{(l)}\right)H^{(l)}\left(u_j^{(l)},:\right)W^{(l)}\right),l=0,\dots ,M-1\text{\hspace{1em}(5)}$$
其中

• $n$表示给定的图中的顶点的数量，用于说明矩阵形式（1）和积分形式（2）之间的归一化化差异

在算法1中，可以在每一个$H^{(l)}$上应用链式法则直接得到对应的batch gradient

3.1 variance reduction 方差缩减

由于所有层都经过了一个非线性变换，因此要计算所有层的方差是一个挑战。文中采用的方式是对于每一个层在进行非线性变换之前改进embedding函数的方差。比如，对于第$l$层，函数${\tilde{h}}_{t_{l+1}}^{(l+1)}(v)$作为卷积$\int \hat{A}(v,u)h_{t_l}^{(l)}(u)W^{(l)}dP(u)$的近似。当采样$t_{l+1}$个样本$v=u_1^{(l+1)},\dots ,u_{t_{l+1}}^{(l+1)}$，${\tilde{h}}_{t_{l+1}}^{(l+1)}(v)$的样本均值可以得到一个方差，该方差捕获了与这一层所造成的最终损失之间的偏差。

分别考虑每一层，并做符号简化

在v和u的联合分布（joint distribution）下，上述样本均值为

$$G:=\frac{1}{s}\sum _{i=1}^{s}y\left(v_i\right)=\frac{1}{s}\sum _{i=1}^s\left(\frac{1}{t}\sum _{j=1}^t\hat{A}\left(v_i,u_j\right)x\left(u_j\right)\right)$$

Proposition 2（命题2）

G允许的方差为

$$\mathrm{Var}\{G\}=R+\frac{1}{st}\iint \hat{A}(v,u{)}^{2}x(u{)}^{2}dP(u)dP(v)\text{\hspace{1em}(6)}$$
其中

$$R=\frac{1}{s}\left(1-\frac{1}{t}\right)\int e(v{)}^{2}dP(v)-\frac{1}{s}{\left(\int e(v)dP(v)\right)}^2\text{ and }e(v)=\int \hat{A}(v,u)x(u)dP(u)$$

• 方差公式（6）由两部分组成，第一部分R几乎没有改进的空间了，第二部分双重积分取决于$u_j$是如何采样的
• 公式（6）是通过概率测度P采样$u_j$的结果
• 可以通过重要性采样改变样本分布，从而减少方差

令$Q(u)$表示新的概率测度，可以定义新的样本均值的近似值

$$y_Q(v):=\frac{1}{t}\sum _{j=1}^t\hat{A}\left(v,u_j\right)x\left(u_j\right)\left(\frac{dP(u)}{dQ(u)}{|}_{u_j}\right)$$

the quantity of interest

$$G_Q:=\frac{1}{s}\sum _{i=1}^s{y}_Q\left(v_i\right)=\frac{1}{s}\sum _{i=1}^s(\frac{1}{t}\sum _{j=1}^t\hat{A}(v_i,u_j)x(u_j)(\frac{dP(u)}{dQ(u)}{|}_{u_j}\left)\right)$$
很显然，$G_Q$的方差和$G$的相同，不用管新的测度$Q$。下面的结果给出了一个最优的的$Q$。

定理3

如果

$$dQ(u)=\frac{b(u)|x(u)|dP(u)}{\int b(u)|x(u)|dP(u)}\text{ where }b(u)={\left[\int \hat{A}(v,u{)}^{2}dP(v)\right]}^{\frac{1}{2}}，\text{\hspace{1em}(7)}$$
那么，$G_Q$的方差

$$\mathrm{Var}\left\{G_Q\right\}=R+\frac{1}{st}{\left[\int b(u)|x(u)|dP(u)\right]}^2，\text{\hspace{1em}(8)}$$
其中

• R和命题2中的一样
• 方差是Q的所有选择中最小的

用这种方式定义采样分布Q的缺点是涉及到$|x(u)|$，它在训练过程中经常改变。这相当于embedding matrix$H^{(l)}$和参数矩阵$W^{(l)}$的乘积。由于参数矩阵在每次迭代过程中都是在更新的，因此矩阵乘法的计算代价是很高的。所以，计算最优的测度Q的代价是很高的。

作为一个折中，考虑一个只涉及$b(u)$的Q。命题4给出了一个精确的定义。最终的方差可能小于公式（6）中的方差。在实际应用中，发现是很有用的。

命题4

如果

$$dQ(u)=\frac{b(u{)}^{2}dP(u)}{\int b(u{)}^{2}dP(u)}$$
其中，$b(u)$按公式（7）的定义。那么，$G_Q$的方差为

$$\mathrm{Var}\left\{G_Q\right\}=R+\frac{1}{st}\int b(u{)}^{2}dP(u)\int x(u{)}^{2}dP(u),\text{\hspace{1em}(9)}$$

• R还是按命题2中的定义。

在概率测度Q下，$dQ(u)/dP(u)$的比值和$b(u{)}^2$成正比，这样就可以简化积分$\hat{A}(v,u{)}^2$。
对给定的图中给定所有顶点定义概率质量函数

$$q(u)=\Vert \hat{A}(:,u){\Vert }^2/\sum _{u^{\prime }\in V}{\Vert \hat{A}\left(:,u^{\prime }\right)\Vert }^2,u\in V$$

• 可以看出上式不依赖于$l$，因此，对所有层的采样分布都是相同的
• 根据这个分布采样t个顶点样本$u_1,...,u_t$

公式（4）中的batch loss$L_{batch}$现在可以重新递归地扩展开

$$H^{(l+1)}(v,:)=\sigma \left(\frac{1}{t_l}\sum _{j=1}^{t_l}\frac{\hat{A}\left(v,u_j^{(l)}\right)H^{(l)}\left(u_j^{(l)},:\right)W^{(l)}}{q\left(u_j^{(l)}\right)}\right),u_j^{(l)}\sim q,l=0,\dots ,M-1.\text{\hspace{1em}(10)}$$
公式（5）和（10）的区别在于前者通过均匀采样获得样本而后者根据概率密度公式q获得样本。

在算法2中，可以在每一个$H^{(l)}$上应用链式法则直接得到对应的batch gradient

3.2 Inference 推理

• 上式采样方法可以很好的把训练数据和测试数据分开
• 这是一种inductive学习的方法，本质上就是将图的顶点集转化成独立同分布（iid）的样本，从而能够在执行参数更新的时候利用loss的一致估计量（consistent estimator）的梯度
• 然后，为了进行推理，可以使用完整的GCN结构(1)计算新顶点的embedding，或者像参数学习中那样通过采样近似。
• 通常，使用完整的GCN结构更直观，更容易实现。

3.2 和GraphSAGE的对比

• GraphSAGE作为一种通过聚合邻居节点的信息来生成节点embedding的方式，由于递归地进行邻居扩展，仍然有内存瓶颈的问题
• 为了减少计算开销，GraphSAGE针对每一层限制中间邻居的数量，使用本文的标记，如果在第$l$层对每个顶点采样$t_l$个邻居，那么GraphSAGE扩展的邻居数量在最坏的情况下就是$t_l$个样本的乘积
  FastGCN 和GraphSAGE的区别在于采样的是图中的顶点而不是邻居。涉及到的总的顶点的数量就是$t_l$的和而不是乘积

4 实验

Benchmark

在GCN和GraphSAGE的基础上做的实验，并和它们进行对比。
benchmark tasks

• 用Cora数据集做主题分类研究
• 用Pubmed数据库分类学术文章
• 用Reddit帖子数据集预测社交网络的社区结构

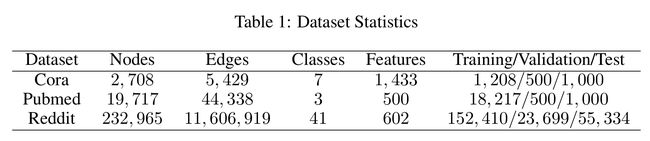
数据集

• 使用调整了training/validation/test的比例的数据集Cora、Pubmed进行有监督学习
• 在GCN中，进行训练的有标签的样本只有很少的一部分，而FastGCN中所有有标签的样本都进行训练
• 这种分割与GraphSAGE中使用的另一个数据集Reddit是一致的
• 使用Cora、Pubmed数据集原始比例进行训练的额外实验可在附录参考

实验细节

• 所有网络只使用两层
• FastGCN的代码来源于GCN，可以参考GCN的源代码

FastGCN中采样的使用

• 表2的“Sampling”列下面显示了随着采样的样本数量的增加，训练时间和分类准确率(as measured by using micro F1 scores)都在增加
• 由于第一层的$\hat{A}{H}^{(0)}$是不变的，这就意味着在链式法则的最后一步关于$W^{(0)}$的梯度是一个常量。因此文中做了一个预先计算乘积的方式而不是对这一层进行采样来提高效率。可以在表2中看到，训练时间有了本质的降低但是准确率却没有太大的变化。
• 后面的所有实验都采用这种预先计算的方式

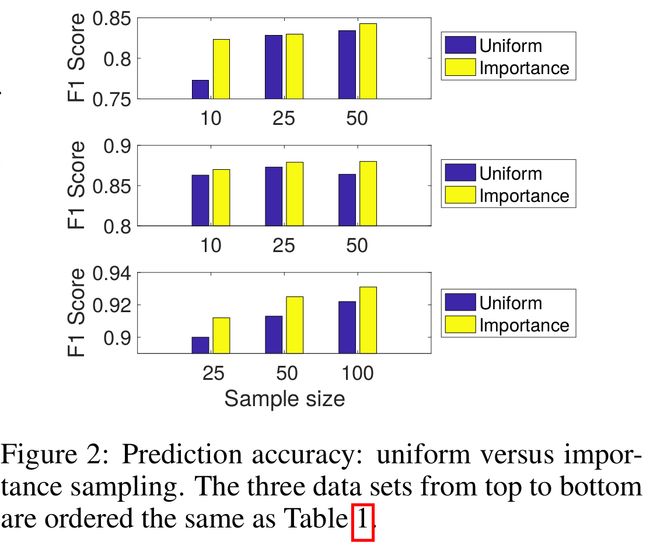
FastGCN中采样方法的对比：均匀采样和重要性采样

• 图2的结果表明，重要性采样比均匀采样始终具有更高的精度。因为改变采样的分布是一种最优化的分布的可选择的折中（见命题4和算法2）
• 结果表明，重要性采样的方差比均匀采样的方差更小，也就是说公式（9）比（6）更接近（8），一个可能原因就是$b(u)$和$|x(u)|$相关。
• 后面的实验均采用重要性采样

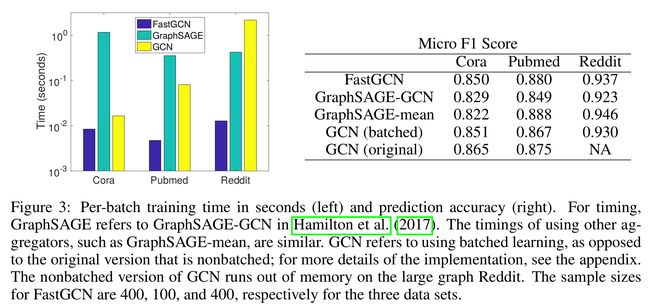
FastGCN的速度和原始GCN和GraphSAGE的对比

• 图3中条形图的高等表示每个batch的训练时间
• GraphSAGE和GCN相比，在小图(Cora and Pubmed)上训练的时间慢一些，但是在大而稠密的图（如Reddit）上速度有了本质的提升
• 从图3中可以看出FastGCN除了在Cora数据集上加速的少一些，在Pubmed和Reddit数据集上都有了很大的提升，和最慢的比，提升了近两个数量级的速度
• FastGCN的训练时间与达到最佳预测精度的样本量有关，FastGCN在三种数据集上的样本量分别是400,100,400

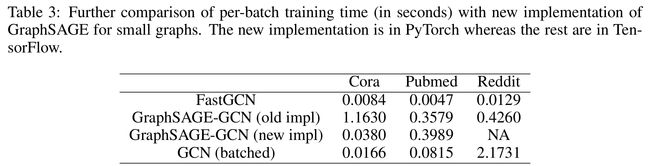
new implementation of GraphSAGE for small graphs

• GraphSAGE适用于大图，因为在小图上的样本数量（乘积的方式）和图的顶点数量是差不多的，因此在小图上的提升有限，并且采样也会增大时间开销
• GraphSAGE的作者为了比较，改了GraphSAGE的代码，减少了采样的节点的冗余计算（GraphSAGE-GCN (new impl)），这样GraphSAGE每个batch的训练时间在最小的图Cora上比较好，但在大图(如Reddit)上不能运行

5 小结

• 提出了一个比GCN更快的inductive的FastGCN，解决了GCN由于递归扩展邻居的内存瓶颈
• 将图卷积重新看作是embedding函数的积分变换的形式
• 和GraphSAGE的邻居采样方式不同，FastGCN中的采样方式是基于给定的图的顶点的，并且是一种重要性采样
• GCN体系结构的简单性允许用积分变换自然地解释图形卷积。然而，这种观点可以推广到许多基于一阶邻域的图模型，其中包括MoNet that applies to (meshed) manifolds (Monti et al., 2017),消息传递网络 (see e.g., Scarselli et al. (2009); Gilmer et al. (2017))
• 当推广到其他网络时，另一项工作是研究方差是否减少是以及如何改进estimator，这可能是未来研究的一个有价值的方向。

了解更多证明和实验细节，可参考论文中的附录部分。