Java实现的LU分解,高斯消去法求线性方程组的解

LU分解在本质上是高斯消元法的一种表达形式。实质上是将A通过初等行变换变成一个上三角矩阵，其变换矩阵就是一个单位下三角矩阵。这正是所谓的杜尔里特算法（Doolittle algorithm）
重点内容
高斯消去法分为
(1)LU分解 (2)前代 (3)回代

实例:题目:a)用高斯消去法解方程组Ax = b,其中

A=⎡⎣⎢⎢24−249−1−2−37⎤⎦⎥⎥

b=⎡⎣⎢⎢2810⎤⎦⎥⎥

b)用得到的A的LU分解,解方程Ay=c

-

LU分解

1.定义
LU分解是矩阵分解的一种,可以将系数矩阵A转变成等价两个矩阵L和U的乘机,其中L和U分别是下三角和上三角矩阵,A = LU.
2.例子
对如下矩阵A,对A进行LU分解

A=⎡⎣⎢⎢24−249−1−2−37⎤⎦⎥⎥

(1)先解出A的上三角矩阵U



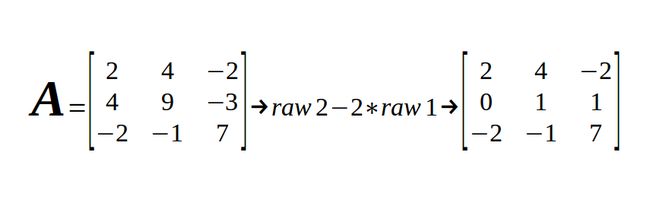
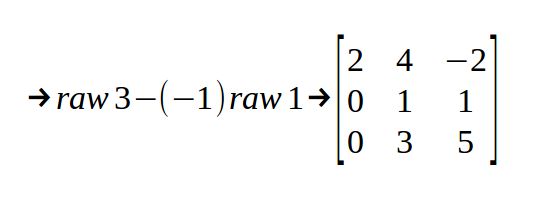
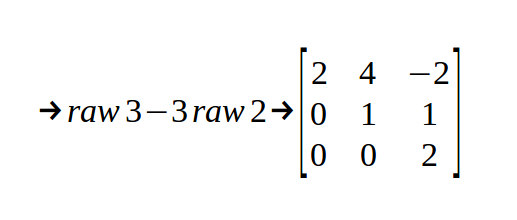
故

U=⎡⎣⎢⎢200410−212⎤⎦⎥⎥

(2)解出A的下三角矩阵L
下三角矩阵L中对应位置的元素就是求解上三角矩阵时对应位置的乘数因子.对应上述矩阵, L21 = 2; L31 = -1; L32 = 3,对角线上的数为1,
故下三角矩阵为:
$$
L = \left[\begin{matrix}1 & 0& 0 \2& 1 & 0 \-1 & 3 & 1 \
\end{matrix} \right]
(3)代码如下

private static List<double[][]> decomposition(double[][]a){
        double[][] U = a;  //a是要分解的矩阵
        double[][] L = createIndentityMatrix(a.length);  

        for(int j=0; j0].length - 1; j++) {             
            if(a[j][j] == 0) {  
                 throw new IllegalArgumentException("zero pivot encountered.");  
             }  

            for(int i=j+1; idouble mult = a[i][j] / a[j][j];   
                for(int k=j; k//得出上三角矩阵U,通过减去矩阵的第一行,第二行,第一行(第二行)得到上三角矩阵
                 }  
                L[i][j] = mult;  //得到下三角矩阵是得出上三角矩阵的乘积因子
            }  
        }  
        return Arrays.asList(L, U);

    }

-

前代

(1)因为LUx = b,

LUx=b

令

Ux=V

则

LV=b

⎡⎣⎢⎢12−1013001⎤⎦⎥⎥.V=⎡⎣⎢⎢2810⎤⎦⎥⎥

V=⎡⎣⎢⎢240⎤⎦⎥⎥

(2)代码如下

 private static double[] getUMultiX(double[][] a, double[] b, double[][] L) {  
        double[] UMultiX = new double[a.length];  
        for(int i=0; i
            double right_hand = b[i];  
            for(int j=0; j
                right_hand -= L[i][j] * UMultiX[j];  //
            }  
            UMultiX[i] = right_hand / L[i][i];  
        }  
        return UMultiX;  
    }  

回代

(1)将得到V代入,得到x

Ux=V

⎡⎣⎢⎢200410−212⎤⎦⎥⎥.x=⎡⎣⎢⎢240⎤⎦⎥⎥

x=⎡⎣⎢⎢−740⎤⎦⎥⎥

(2)代码如下

private static double[] getSolution(double[][] a, double[][] U,  
            double[] UMultiX) {  
        double[] solutions = new double[a[0].length];  
        for(int i=U.length-1; i>=0; i--) {  
            double right_hand = UMultiX[i];  
            for(int j=U.length-1; j>i; j--) {  
                right_hand -= U[i][j] * solutions[j];  
            }  
            solutions[i] = right_hand / U[i][i];  
        }  
        return solutions;  
    }  

 - 

如果不够清楚,可以看下方总体代码

import java.util.Arrays;
import java.util.List;

public class Decomposition {

    public static void main(String[] args) {
        double [][]A ={{2,4,-2},{4,9,-3},{-2,-1,7}};
        double []b = {2,8,10};
        int row = 3;
        double[]x = solve(A, b);
        for(int i = 0;ipublic static double[] solve(double[][] a, double[] b) {          
        List<double[][]> LAndU = decomposition(a);  //LU decomposition  
        double[][] L = LAndU.get(0);  
        double[][] U = LAndU.get(1);  
        double[] UMultiX = getUMultiX(a, b, L);   //前代    
        return getSolution(a, U, UMultiX);        //回代
    }  

    /** 
     * Get solution of the equations 
     * @param a - Coefficient matrix of the equations 
     * @param U - U of LU Decomposition 
     * @param UMultiX - U multiply X 
     * @return Equations solution 
     */  
    private static double[] getSolution(double[][] a, double[][] U,  
            double[] UMultiX) {  
        double[] solutions = new double[a[0].length];  
        for(int i=U.length-1; i>=0; i--) {  
            double right_hand = UMultiX[i];  
            for(int j=U.length-1; j>i; j--) {  
                right_hand -= U[i][j] * solutions[j];  
            }  
            solutions[i] = right_hand / U[i][i];  
        }  
        return solutions;  
    }  

    /** 
     * Get U multiply X 
     * @param a - Coefficient matrix of the equations 
     * @param b - right-hand side of the equations 
     * @param L - L of LU Decomposition 
     * @return U multiply X 
     */  
    private static double[] getUMultiX(double[][] a, double[] b, double[][] L) {  
        double[] UMultiX = new double[a.length];  
        for(int i=0; idouble right_hand = b[i];  
            for(int j=0; j//
            }  
            UMultiX[i] = right_hand / L[i][i];  
        }  
        return UMultiX;  
    }  

    private static List<double[][]> decomposition(double[][]a){
        double[][] U = a;  //a是要分解的矩阵
        double[][] L = createIndentityMatrix(a.length);  

        for(int j=0; j0].length - 1; j++) {             
            if(a[j][j] == 0) {  
                 throw new IllegalArgumentException("zero pivot encountered.");  
             }  

            for(int i=j+1; idouble mult = a[i][j] / a[j][j];   
                for(int k=j; k//得出上三角矩阵U,通过减去矩阵的第一行,第二行,第一行(第二行)得到上三角矩阵
                 }  
                L[i][j] = mult;  //得到下三角矩阵是得出上三角矩阵的乘积因子
            }  
        }  
        return Arrays.asList(L, U);

    }
    private static double[][]createIndentityMatrix(int row){
        double[][]identityMatrix = new double[row][row];
        for(int i=0;ifor(int j=i;jif(j==i){
                    if (j==i) {
                        identityMatrix[i][j]= 1;
                    }else {
                        identityMatrix[i][j] = 0;
                    }
                }
            }
        }
        return identityMatrix;
    }
}