leetcode-5-回文数

关于算法的选择以及评估问题，请看-----；

简单的介绍一下：
回文数，其实上大学应该会介绍该内容。如果一个字符串可能就是就既定的（要么是回文串要么不是回文串）。那么问题还是比较简单的。
但是现在给你一个字符串，找出其中字符串的最长回文子串。这里讲一讲leetcode的第五题：

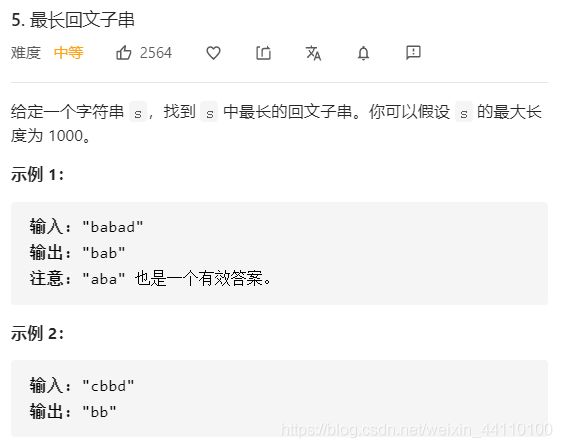
5. 最长回文子串

常规做法：没有涉及多少的算法思想，如果算是算法思想的话。双指针算不算呢？

思路如下：如果采用暴力枚举的话，好像居然过去了？

要分成就情况，如果abcba，abccba那么就要分情况了。
for(int i=0;i ①：从一开始去进行选择，对单个字符的左右去进行比对。
比如：rabcbak，这是一个奇数个字符构成的字符串，那么我们就可以按奇数个具体双指针比对。 知道左右比对不相等，那么就可以截取去长度.假设我们移动的长度为i
那么长度length=(r-1)-(l-1)+1=r-l-1,这里不要理解错。
那么我们很容易去写出代码了。

完整的在dev的代码如下：

#include 
using namespace std;
string longestPalidrome(string s){
	//这里去进行补充
	string res;//定义一个答案
	//对于单个字符串 ,设置左右两边的双指针 
	for(int i=0;i<s.size();i++){
		int l=i-1,r=i+1;
		//左右去进行扫描 
		while(l>=0&&r<=s.size()&&s[l]==s[r]) l--,r++;
		//满足了成立条件，去除回文子串 
		if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
		
		//如果是偶数串
		l=i,r=i+1;
		//左右去进行扫描 
		while(l>=0&&r<=s.size()&&s[l]==s[r]) l--,r++;
		if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
	} 
	return res; 
}
int main(){
	string str;
	cin>>str;
	string s=longestPalidrome(str);
	cout<<s; 
	return 0;
}

在leetcode的结果如下：

class Solution {
public:
    string longestPalindrome(string s) {
        	//这里去进行补充
	string res;//定义一个答案
	//对于单个字符串 ,设置左右两边的双指针 
	for(int i=0;i<s.size();i++){
		int l=i-1,r=i+1;
		//左右去进行扫描 
		while(l>=0&&r<=s.size()&&s[l]==s[r]) l--,r++;
		//满足了成立条件，去除回文子串 
		if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
		
		//如果是偶数串
		l=i,r=i+1;
		//左右去进行扫描 
		while(l>=0&&r<=s.size()&&s[l]==s[r]) l--,r++;
		if(res.size()<r-l-1) res=s.substr(l+1,r-l-1);
	} 
	return res; 
    }
};

双指针的做法其实算法复杂度已经在O(n^2)了。

因为刚刚入门动态规划，还是尽力尝试用dp去做一下：
还是提前说一下，使用动态规划的前提：重叠子问题和最优子结构。我们希望找到重叠关系以及边界条件，这样我们可以不至于一直循环下去。
动态规划的两个条件：状态方程和状态条件

这里参考《算法笔记》11.5最长回文子串。
简单描述最长回文子串的dp解决方案的思想：我们不妨称该字符串为s。且回文子串的下表范围为[i,j]。我们期望不断缩小规划，然后在边界的时候结束比较。
与上面的双指针往外去进行比较相比，dp是向内的。
①：如果s[i]==s[j],且s[i]_{s[j]里面也是回文子串，那么从i到j，该串也是回文子串。如果s[i]}s[j]不是回文子串，那么s[i]~s[j]也一定不是回文子串
②：如果s[i[!==s[j],那么s[i]~s[j]也一定不是回文子串。

那么我们可以总结一下状态方程和状态条件了

$$dp[i][j]=\{\begin{array}{ll}dp[i+1][j-1],s[i]==s[j]& \\ 0(0表示不是回文串)& \text{s[i]！=s[j]}\end{array}$$

以leetcode的53为底子，按照状态方程和状态条件很容易就写出来了。

…先去吃饭，一会儿补上来