算法与程序设计基础略讲(附带洛谷例题)
前言
这篇文章改编自我的选修课“算法与程序设计”课程报告,我将里面的大部分例子换成了洛谷上的例题,适合给想入门程序设计竞赛(oi,ACM)或者刚接触计算机编程不久的人看。其实我也只是一位大自然的搬运工,里面的许多代码都不是我自己的....所以如果有冒犯,请联系我,我立刻整改。这里十分感谢gin同学,他为这篇文章打下了框架和脉络,我也只是在他工作的基础之上进行了微微的修饰。
目录
1. 第一章 程序设计概述.
2. 第二章 算法的表述方式.
3. 第三章 结构化程序设计思想概述.
3.1 结构化程序设计思想简述.
3.2 结构化程序设计实例及其分析.
4. 第四章 构造类型概述.
4.1 常见的构造类型定义及其特点.
4.2 构造类型在程序中的实例及其分析.
5. 第五章 动态数据结构概述.
5.1 动态数据结构定义及其特点.
5.2 动态数据结构的基本类型和在程序中的实例及其分析.
6. 第六章 分治法概述与分析.
6.1 分治法的基本思想.
6.2 实例及其分析.
7. 第七章 常见查找和排序算法.
7.1 查找算法.
7.2 排序算法.
8. 第八章 动态规划算法概述与分析.
8.1 动态规划算法的基本思想.
8.2 实例及其分析.
9. 第九章 贪心算法概述与分析.
9.1 贪心算法的基本思想.
9.2 实例及其分析.
10. 第十章 回溯法概述与分析.
10.1 回溯法的基本思想.
10.2 实例及其分析.
11. 第十一章 随机算法概述与分析.
11.1 随机算法的基本思想.
11.2 实例及其分析.
1. 第一章 程序设计概述
程序设计:人们借助计算机可以理解的语言编写程序,用以告诉计算机应该处理哪些数据和如何来处理数据。而能够用于构造程序的指令集合,被称为程序设计语言(programming language)。
程序设计语言:
1.1机器语言
机器语言是指由二进制代码按照一定规则组成的命令集合,也称为机器指令集合。机器语言是唯一能被计算机直接理解和执行的程序设计语言。机器语言的每一条语句实际上是一条机器指令,它以二进制形式表示,书写时为了方便经常使用十六进制形式。缺点是难以记忆,可读性和移植性差。
1.2汇编语言
人们把机器指令用英文助记符合符号地址来表示,这种助记符语言称为汇编语言。
汇编语言语句命令是跟机器语言指令一一对应的。汇编语言编写的程序,必须经过汇编器(assembler)翻译成计算机可以识别的机器指令后才能在计算机上执行。
1.3高级语言
高级语言是更接近人类的自然语言和数学语言的表示方法,具有更强的表达能力。
高级语言的出现使得计算机程序设计语言不再过度地依赖某种特定的机器或环境。这是因为高级语言在不同平台上可以被编译成不同的机器语言,而不是直接被机器执行。
程序设计语言的发展历史:
现代计算机的程序由采用数字编码的指令序列组成。这样的编码系统称为机器语言。但是,用机器语言编写程序是一项冗长乏味的任务,而且经常出错。
20世纪40年代,研究人员为了简化程序设计过程开发了计数制系统,使得指令可以用助记符表示,不用使用数字形式表示。建立起助记符系统后,人们就开发了称为汇编器的程序,用来将助记符表达式转换为机器语言,而不必直接使用机器语言开发程序。实际上,汇编语言的出现是革命性的事件,以至于它们被称为第二代程序设计语言,而第一代程序设计语言就是机器语言本身。
尽管汇编语言与它们对应的机器语言相比有不少优势,但是仍有一些不足——它们没有提供最终的程序设计环境,换言之,用汇编语言写的程序必须依赖于机器。因此,计算机科学家开始开发比低级的汇编语言更易于开发软件的程序设计语言。结果就出现了第三代程序设计语言,它们的原语不仅级别更高,而且都是机器无关的。最著名的早期例子是FORTRAN和COBOL,前者是为科学和工程应用开发的,后者是由美国海军为商业应用开发的。
C语言的发展历史:
C语言的原型是ALGOL 60算法语言,由图灵奖获得者艾伦.佩利(Alan J. Perlis)在巴黎举行的世界软件专家讨论会上发布,它也被称为A语言。
1963年,剑桥大学将ALGOL 60语言发展成为CPL语言。
1967年,剑桥大学的Matin Richards对CPL语言进行了简化,于是产生了BCPL语言。
1970年,Ken Thompson将BCPL进行了修改,并为它起名为B语言。
1972年,美国贝尔实验室的D.M.Ritchie在B语言的基础上最终设计出了一种新的语言,这就是C语言。
1973年,C语言的主体完成。Thompson和Richards开始用它完全重写了UNIX。随着UNIX的发展,C语言自身也在不断地完善。直到今天,各种版本的UNIX内核和周边工具仍然使用C语言作为最主要的开发语言。
小结:程序设计语言随着计算机科学技术的发展而发展,并不断完善。程序设计语言分为高级语言和低级语言,而高级语言更接近人类语言的表达方式。
2. 第二章 算法的表述方式及其发展
算法的常见表述方式及其优缺点
算法的概念:算法是定义一个可终止过程的一组无歧义的、可执行的步骤的有序集合。
算法的表述:
2.1 自然语言
使用人们日常使用的语言来描述算法。
优点:通俗易懂,容易掌握。
缺点:容易产生歧义,缺乏直观性。
2.2 流程图:
使用一些几何图形、线条以及文字说明来描述算法的逻辑结构。
优点:清晰直观,没有歧义。
缺点:难以阅读和修改。
2.3 N-S图
这种流程图完全去掉了流程线,算法的每一步都用一个矩形框来描述,把一个个矩形框按执行的次序连接起来就是一个完整的算法描述。
优点:易学易用。
缺点:难以修改。
2.4 PAD图
使用二维树形结构图表示程序的控制流,遵循机械的走树规则。
优点:比较容易转换成程序代码。
缺点:不如流程图易执行。
2.5 伪代码
通常采用自然语言短语、数学公式和符号来描述算法步骤的操作步骤,同时采用计算机高级语言的控制结构来描述算法步骤的执行顺序。
优点:简洁易懂。
缺点:不够直观。
小结:算法的表述方式包括自然语言、流程图、伪代码等,表述方式各有其优缺点。
3. 第三章 结构化程序设计思想概述
3.1 结构化程序设计思想简述
为了解决大量跳转语句使得程序的流程变得复杂的问题,结构化程序设计的概念最早由Edsger Wybe Dijkstra在1965年提出。它的主要观点是采用自顶向下、逐步求精及模块化的程序设计方法;使用三种基本控制结构构造程序,任何程序都可由顺序、选择和循环三种基本控制结构构造; 而且他还提出了go to有害论,因为这样会破坏程序的结构性。
3.2结构化程序设计实例及其分析
掉入陷阱的数字(PTA 中M2017秋C入门和进阶练习集7-31)
对任意一个自然数N0,先将其各位数字相加求和,再将其和乘以3后加上1,变成一个新自然数N1;然后对N1重复这种操作,可以产生新自然数N2;……多次重复这种操作,运算结果最终会得到一个固定不变的数Nk,就像掉入一个数字“陷阱”。
本题要求对输入的自然数,给出其掉入“陷阱”的过程。
输入格式:
在一行内给出一个自然数N0(N0<30000)。
输出格式:
对于输入的N0,逐行输出其掉入陷阱的步骤。第i行描述N掉入陷阱的第i步,格式为:i:Ni(i≥1)。当某一步得到的自然数结果Nk(k≥1)与上一步Nk−1相同时,停止输出。
实现代码:
#include
#include
int main()
{
int a[100];//用以储存新的自然数
scanf("%d",&a[0]);
int sum=0,i=1,t=a[0];
while(t)//如果t不为0,则逐步累加自然数的各个位数
{
sum+=t%10;
t/=10;
}
a[i]=3*sum+1;//求出新的自然数
while(a[i]!=a[i-1])//如果新的自然数没有掉入陷阱
{
printf("%d:%d\n",i,a[i]);
i++;
sum=0;//重置累加器为0
t=a[i-1];
while(t) // 继续求出新的自然数
{
sum+=t%10;
t/=10;
}
a[i]=3*sum+1;
}
printf("%d:%d\n",i,a[i]);
} 分析:上述实例充分体现了结构化程序设计的思想,利用顺序、选择和循环三种基本控制结构,将自然数掉进陷阱的过程表述出来。
小结:结构化程序设计的思想是自顶向下、逐步求精,三种基本结构是顺序、选择和循环。
4. 第四章 构造类型概述
4.1 常见的构造类型定义及其特点
构造类型:
在实际应用中,我们往往需要把有关联的数据组合在一起使用,这种组合数据的值就能够被分解成独立的数据元素,程序可以通过一种特定的定位方法来独立地访问。这种组合起来的数据类型称之为构造类型。
数组:
数组用于保存和处理一组具有相同类型的数据,形成一个逻辑组合并通过统一的名字进行访问。数组里的每项数据成为数组的元素,每一个元素在内存中是紧接着按序存储,每一个元素的访问通过相同的数组名称并使用一个称为数组下标的位置号来定位。
字符串:
字符串存储在连续的空间里,本质上是一个字符数组,以结束符‘\0’作为分界判断。
结构体:
结构体类型是由不同类型的数据项组成的构造类型。组成结构体类型的每一个数据项称为该结构体的成员,通过‘.’操作符访问。结构体体现了面向对象编程的部分特点。
共用体:
共用体类型与结构体类型相似,但是它们的存储方式不同,结构体类型的每个成员都有自己的内存空间,而共用体类型的所有成员公用同一段内存空间。因此,程序运行中的某一时刻共用体类型中只能有一个成员起作用。
枚举:
枚举类型是一种值由程序员列出的类型,并且程序员必须为每个值命名,这个值叫做枚举常量。
4.2 构造类型在程序中的实例及其分析
数组举例:
陶陶摘苹果(洛谷P1046)
陶陶家的院子里有一棵苹果树,每到秋天树上就会结出1010个苹果。苹果成熟的时候,陶陶就会跑去摘苹果。陶陶有个3030厘米高的板凳,当她不能直接用手摘到苹果的候,就会踩到板凳上再试试。
现在已知1010个苹果到地面的高度,以及陶陶把手伸直的时候能够达到的最大高度,帮陶陶算一下她能够摘到的苹果的数目。假设她碰到苹果,苹果就会掉下来。
实现代码:
#include//万能头文件
int a[11];//定义全局变量。
int main(){//主函数 long long n,tt,sum=0;/*定义一个sum作为陶陶摘到的数量。n表示陶陶的身高。*/
for(register long long i=0;i<10;i++)/*循环输入数组。至于register这个东东是用来加速的。*/
scanf("%lld",&a[i]);//输入每一个苹果的高度
scanf("%lld",&n); //输入陶陶的身高
tt=n+30;//陶陶能够到的最高高度。
for(register long long j=0;j<10;j++) {
if(tt>=a[j])//循环判断,把a[0]到a[10]能否够到判断完。
sum++;//累加器,如果大于则可行解+1
}
printf("%lld",sum);//输出sum即可。
return 0;
} 分析:10个数据如果全部用变量存储不太方便,用数组反而会更加简单。
字符串举例:
寻找字符串(SCAUOJ 1050)
由键盘输入两个字符串(假设第一个字符串必包含第二个字符串,如第一个字符串为ABCDEF,第二个为CDE,
则CDE包含在ABCDEF中),现要求编程输出第二字符串在第一行字符串中出现的位置。
(如果第二个字符串在第一个字符串中出现多次,则以最前出现的为准)
实现代码:
#include
#include
#include
int main()
{
int i,j;
char a[20],b[20];
gets(a);
gets(b);
for(i=0; a[i]!='\0'; i++)//枚举i,a从第i位开始比较
{
for(j=0; b[j]!='\0'; j++)
{
if(a[i+j]!=b[j]) break;//发现有不相同的字符
}
if(b[j]=='\0') break;//代表比较完毕
}
printf("%d",i+1);
return 0;
} 分析:用两个字符数组存储字符串,再对两个字符数组进行比较,如果比较完后第二个字符串为结束符'\0',则说明第二个字符串完全包含在第一个字符串中,此时第一个字符的位置则对应第一个字符串的位置。
结构体举例:
学生成绩表(SCAUOJ 18059)
输入10个学生,每个学生的数据包括学号、姓名、3门课的成绩。定义结构体类型表示学生类型,输入10个学生的数据,
计算每个学生的平均成绩。按平均成绩由高到低输出所有学生信息,成绩相同时按学号从小到大输出。
实现代码:
#include
#include
struct data
{
int num;//学生的学号
char name[20];//学生的姓名
double score[3];//学生的科目成绩
double ave;//平均分
};
int main()
{
int i,j;
struct data stu[10],tmp;
for(i=0; i<10; i++)
{
scanf("%d%s%lf%lf%lf",&stu[i].num,stu[i].name,stu[i].score,stu[i].score+1,stu[i].score+2);
stu[i].ave=stu[i].score[0]+stu[i].score[1]+stu[i].score[2];
}
for(i=0; i<9; i++)//冒泡排序
for(j=0; j<9-i; j++)
{
if(stu[j].ave 分析:学生的信息中包含着多种不同类型的数据,如学号、姓名和成绩,因此要定义一个结构体类型data,并定义一个data类型的数组stu存储学生信息,再对其中的成员score作为基准进行了冒泡排序。
共用体举例:
#include
union REC
{
char key;
int number;
double salary;
}uRec;
int main()
{
uRec.key='A';
printf("赋值'A'给成员key,则");
printf("key=%c,number=%d,salary=%6.2f",uRec.key,uRec.number,uRec.salary);
uRec.number=100;
printf("\n赋值100给成员number,则");
printf("key=%c,number=%d,salary=%6.2f",uRec.key,uRec.number,uRec.salary);
uRec.salary=12345.67;
printf("\n赋值12345.67给成员salary,则");
printf("key=%c,number=%d,salary=%6.2f",uRec.key,uRec.number,uRec.salary);
return 0;
} 分析:这三个成员所引用的空间相同,仅有的区别在于每个成员的类型决定了这些空间里的字节被如何解释。因为某个时刻只有一个成员是有效的,程序员要确保在某个时刻使用正确的成员名称来引用当前存在这个共用体中的数据。
枚举举例:
定义一个枚举类型表示考试的结果(通过、失败)。从键盘输入一个成绩,判断该成绩属于哪一种考试结果。
源代码如下:
分析:对于考试的结果,只有pass和failure两种情况,因此可以枚举这两种情况。
小结:构造类型可以把有关联的数据组合在一起使用,主要有数组、字符串、结构体、共用体和枚举等,使用构造类型可以让程序变得更加简洁明了。
5.第五章 动态数据结构概述
5.1 动态数据结构定义及其特点
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
5.2 动态数据结构的基本类型和在程序中的实例及其分析
线性表:
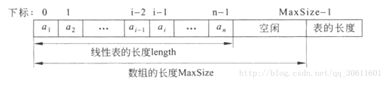
线性表(Linear List)是由同一类型的数据元素构成的有序序列的线性结构。线性表中元素的个数称为线性表的长度;当一个线性表中没有元素时,称为空表;表的起始位置称为表头,表的结束位置称为表尾。
实例:约瑟夫问题(洛谷P1996)
约瑟夫是一个无聊的人!!!n个人(n<=100)围成一圈,从第一个人开始报数,数到m的人出列,再由下一个人重新从1开始报数,数到m的人再出圈,……依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
代码:
#include
#include
using namespace std;
int main()
{
int n,m,s=0;scanf("%d%d",&n,&m);//入读
vector visit(n+1,0);//visit赋初始值
for(int k=0;kn)s=1;if(visit[s])i--;}//类似取模,而因为序列是从1开始的,所以不取模,加判断;若visit过,则i--,使其继续循环
printf("%d ",s);visit[s]=true;//输出,记录已出队
}
return 0;
} 分析:按照题意去做,用一个长度为n+1的visit线性表(其实是vector)记录下已经出队了的人,然后模拟,一个个的加就行了。还要注意,一开始,加的数要赋值为0。还有visit数组要开始全部赋值为false。
总结:在实际情况下,我们往往使用数组作为线性表来使用。C++的stl里更是提供了vector(不定长数组)类,非常方便。有序的储存在内存里是线性表的特点,所以它能够以o(1)的速度访问任意一个元素。同样的,线性表的插入与删除操作非常耗时。
链表:
链表可以存储多个同类型的数据,它是动态地进行存储分配的一种数据结构。结点是链表的基本存储单位,一个结点对应链表中的一个数据元素,所有的结点具有相同的数据结构。每个结点占用一段连续内存空间,而结点间可以占用不连续的内存空间。结点与结点间使用指针链接在一起。
实例:
依然是刚才的“约瑟夫问题”
代码:
#include
using namespace std;
struct peo
{
int ID; //编号
peo *next = NULL, *front = NULL;
}n[100];
void _cut(peo *num)
{
num = num->front;
num->next = num->next->next;
num = num->next;
num->front = num->front->front;
}
int main()
{
int tot, outNum, nowNum = 1;
peo *now = &n[0]; //指向目前报数的人的指针
cin >> tot >> outNum; //数据读入
for (int i = 1; i < tot - 1; i++) { n[i].front = &n[i - 1]; n[i].next = &n[i + 1]; n[i].ID = i + 1; }
n[0].front = &n[tot - 1]; n[0].next = &n[1]; n[tot - 1].front = &n[tot - 2]; n[tot - 1].next = &n[0];
n[0].ID = 1; n[tot - 1].ID = tot;
//初始化链表
while (tot > 0)
{
if (nowNum == outNum)
{
cout << now->ID << " "; //输出出局的人的编号
_cut(now); //出局
nowNum = 1; //初始化数字
tot--; //总人数-1
now = now->next; //下一个人
}
else
{
nowNum++; //数字+1
now = now->next; //下一个人
}
}
return 0;
} 分析:这个例子创建了一个首位相连的链表,直接模拟即可。
总结:链表的特点是可以在内存里以非连续的方式来存储元素信息,所以它能在o(1)的时间内实现插入与删除功能。同样的,它无法直接的访问链表里的一个特点元素。
栈:
栈是一种受限定的线性表,它只允许在线性表的同一端做线性表操作。通常将栈允许操作的一端称为栈顶,而不允许操作的另一端称为栈底;不含元素的空表称为空栈;向栈顶插入元素的操作称为进栈或入栈,而删除栈顶元素的操作称为退栈或出栈。栈的操作是一种后进先出的操作。
实例:表达式括号匹配(洛谷P1739)
假设一个表达式有英文字母(小写)、运算符(+,—,*,/)和左右小(圆)括号构成,以“@”作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则返回“YES”;否则返回“NO”。表达式长度小于255,左圆括号少于20个。
代码:
#include
#include
#include
using namespace std;
stack zhan;
int main() {
char input;
while(scanf("%c",&input)&&input!='@') {
if(input=='(') zhan.push(input);//入栈
if(input==')') {
if(zhan.empty()) {//判断栈是否为空即可
printf("NO\n");
return 0;//至于为啥要判断栈是否为空,大家想想,因为假如有个),结果前面没有对应(了,那就不行,此时就是栈空
}
zhan.pop();//出栈
}
}
if(zhan.empty()) printf("YES\n");//判断有没有多余的(
else printf("NO\n");//也就是判断栈是否为空
return 0;
} 分析:括号的匹配就是一个栈的操作过程,每读入一个“(”就入栈一次,每读入一个“)”就出栈。栈的操作是一种后进先出的操作。在处理递归回溯等问题上,计算机便使用了栈来储存每个函数的信息。
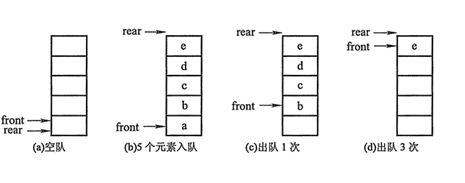
队列:
队列也是一种受限制的线性表,但队列的插入和删除操作是分别在线性表的两个不同端点进行的。允许插入数据的一端称为队尾,而允许删除数据的一端称为队头。
实例:依然是“约瑟夫问题”
代码:
#include
#include
using namespace std;
int main()
{
int tot, outNum, nowNum = 1;
queue q;
cin >> tot >> outNum; //读取数据
for (int i = 1; i <= tot; i++)q.push(i); //初始化队列
while (!q.empty()) //在队列不为空时继续模拟
{
if (nowNum == outNum)
{
cout << q.front() << " "; //打印出局的人的编号
q.pop(); //出局
nowNum = 1; //初始化现在的数字
}
else
{
nowNum++;
q.push(q.front()); //排至队尾
q.pop();
}
}
cout << endl;
system("pause");
return 0;
} 分析:队列是一种先进先出的数据结构。在一些搜索算法比如广度优先搜索里,便使用了队列在存储临时信息。
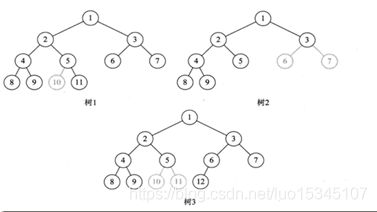
树:
树是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
每个节点有0个或多个子节点;没有父节点的节点称为根节点;每一个非根节点有且只有一个父节点;除了根节点外,每个子节点可以分为多个不相交的子树。
实例:FBI树(洛谷 P1087)
代码:
#include
#include
#include
using namespace std;
int n,ch[2049]={0},m;
string ch2;
//n是叶子有n个节点,m是整棵树有m个节点
//ch用来存节点是F(2)或B(0)I(1)
//ch2是最开始输入的字符串
//这个dg函数s是层数,ll是树的第ll个节点
int dg(int s,int ll)
{
if(s==n+1) return ch[ll];
int a=dg(s+1,ll*2),b=dg(s+1,ll*2+1);
//满二叉树某节点左孩子编号是节点编号*2,右孩子*2+1
if(a==b&&a==1) ch[ll]=1;
if(a==b&&a==0) ch[ll]=0;
if(a==b&&a==2) ch[ll]=2;
if(a!=b) ch[ll]=2;
return ch[ll];
}
//last函数是后续遍历,ll是当前递归到的节点
void last(int ll)
{
if(ll>m) return;
last(ll*2);
last(ll*2+1);
if(ch[ll]==0) cout<<"B";
if(ch[ll]==1) cout<<"I";
if(ch[ll]==2) cout<<"F";
}
int main()
{
cin>>n;
m=pow(2,n)*2-1;
cin>>ch2;
for(int i=0;i 分析:这道题使用了数组来储存一个树结构,并且直接模拟。从根开始找孩子的值(f是2,b是0,i是1),再用孩子的值来推出根的值。因为是满二叉树,所以某节点的左孩子是某节点乘二,右孩子乘二加一。
总结:树是一种常见的数据结构,一些常见的信息比如上下级关系、优先级关系、家庭成员关系都能用树来储存。
图:
图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。在图中的数据元素,我们称之为顶点,顶点集合有穷非空。在图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
实例:信息传递(洛谷P2661)
代码:
#include
#include
#include
#include
#include
#include
using namespace std;
int dx[300000];//存每一个人传话的对象
bool visit[300000]={0},novisit[300000]={0};//visit存每次查找中被查到的点,而novisit存每次查找前,已经被查找过的点(及不用继续查找了)
int bs[300000]={0};//每次查找中第一次到一个节点所经过的边数
int minn=2e9;
void dfs(int node,int num)
{
if(novisit[node])return;//不需要继续找了
if(visit[node])//在此次查找中出现过
{
minn=min(minn,num-bs[node]);//形成一个环,取最小值
}
else
{
visit[node]=true;//在此次循环中经过
bs[node]=num;//记录第一次到达时的步数
dfs(dx[node],num+1);//搜索
novisit[node]=true;//已经搜过
}
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&dx[i]);
}
for(int i=1;i<=n;i++)
{
dfs(i,0);//枚举全部节点
}
printf("%d",minn);//输出
return 0;//时间复杂度O(n)
} 分析:可以把这些关系看成一个有向图。对于任意一个节点进入,因为每个点的出度均为1,所以最多只能构成三种情况:1、一条链;2、一个环链;3、一条链连接着一个环链。因为这三种情况极为的简单,所以就可以如下处理:找任意一个点进入,记录到达每一个点所走过的遍数。当走到一个在这次查找中已经出现过的节点,即找到了一个环,用当前走到的步数减去在此节点原先记录的步数,便得到这个环的长度。由此搜遍所有点,找到这些环中最小长度的一个,并把它输出就可以了。
总结:图也是一种常见的数据结构,它可以用来存储如地图、信息中转站、网络等信息。
小结:常用的数据结构有线性表、链表、栈、队列、树和图等,其中链表、栈和队列属于线性表,而树和图是非线性数据结构。
6. 第六章 分治法概述与分析
6.1 分治法的基本思想
分治法的基本思想是将一个复杂的问题分解成规模较小的相同的子问题,再将子问题分解成更小的子问题,直到子问题可以直接求解,即分而治之。
一般来说,分治法和递归密不可分,通过两者的结合,可以将子问题的解合并成原问题的解。
6.2 实例及其分析
巡逻的士兵(SCAUOJ 1142)
有N个士兵站成一队列, 现在需要选择几个士兵派去侦察。
为了选择合适的士兵, 多次进行如下操作: 如果队列超过三个士兵, 那么去除掉所有站立位置为奇数的士兵,
或者是去除掉所有站立位置为偶数的士兵。直到不超过三个战士,他们将被送去侦察。现要求统计按这样的方法,
总共可能有多少种不同的正好三个士兵去侦察的士兵组合方案。
注: 按上法得到少于三士兵的情况不统计。
1 <= N <= 2的32次方-1
实现代码:
#include
#include
unsigned choose(unsigned n)
{
int remove_odd,remove_even,sum;// remove_odd代表去掉位置为奇数士兵后问题的答案,是原问题的子问题,remove_even同理。
if(n==3) return 1;
else if(n<3) return 0;
else
{
if(n%2==0)//当n为偶数时,去掉奇数的人和去掉偶数的人都是少了n/2的人
{
remove_odd=choose(n/2);
remove_even=choose(n/2);
}
else//当n为奇数时再分开来讨论
{
remove_odd=choose((n+1)/2);
remove_even=choose((n-1)/2);
}
sum=remove_odd+remove_even;//合并两个子问题
return sum;
}
}
int main()
{
unsigned n;
scanf("%u",&n);
printf("%d\n",choose(n));
return 0;
} 分析:将一个大的士兵数N逐步分解为若干个类型相同的子问题求解,直到子问题的士兵数小于或等于3为止,再用递归的方法把子问题的解合并。
小结:分治法的精髓:
分--将问题分解为规模更小的子问题;
治--将这些规模更小的子问题逐个击破;
合--将已解决的子问题合并,最终得出“母”问题的解。
7. 第七章 常见查找和排序算法
7.1 查找算法
顺序查找:
顺序查找是在一个已知无(或有序)序队列中找出与给定关键字相同的数的具体位置。
实现代码:
int sq_search(keytype keyp[],int n,keytype key)
{
int i;
for(i=0; i分析:顺序查找的时间复杂度为o(n),适用于难以进行位置调换或信息修改的数据。
二分查找:
二分查找又叫折半查找,指的是每次的查找范围折半。
实现代码:
int binSearch(const int *Array,int start,int end,int key)
{
int left,right;
int mid;
left=start;
right=end;
while(left<=right)
{
mid=(left+right)/2;
if(key==Array[mid]) return mid;
else if(keyArray[mid]) left=mid+1;
}
return -1;
} 分析:比较次数少,查找速度快,但序列必须是有序的。每次比较后,带查找的范围都会变为原来的1/2,所以时间复杂度为o(logn)。
7.2 排序算法
选择排序:
选择排序是指每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
实现代码:
int main()
{
int i,j,min,t;
for(i=0;ia[j])
min=j;//交换
if(min!=i)
{
t=a[min];
a[min]=a[i];
a[i]=t;
}
}
} 分析:选择排序是不稳定的排序方法。时间复杂度最坏时为o(n^2)。
插入排序:
插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据。
实现代码:
voidinsert_sort(int*array,unsignedintn) {
inti,j;
inttemp;
for(i=1; i0&&*(array+j-1)>temp; j--) {
*(array+j)=*(array+j-1);
}
*(array+j)=temp;
}
} 分析:插入排序适用于少量数据的排序,是稳定的排序方法。时间复杂度为o(n^2)。
冒泡排序:
冒泡排序是指重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
实现代码:
void bubble_sort(int a[], int n)
{
int i, j, temp;
for (j = 0; j < n - 1; j++)
for (i = 0; i < n - 1 - j; i++)
{
if(a[i] > a[i + 1])
{
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
} 分析:比较相邻的元素。如果第一个比第二个大,就交换他们两个。对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。时间复杂度为o(n^2)。
快速排序:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
实现代码:
void sort(int *a, int left, int right)
{
if(left >= right)
{
return ;
}
int i = left;
int j = right;
int key = a[left];//选取一个分割的比较基准,基准的选取直接影响到排序的速度
while(i < j)
{
while(i < j && key <= a[j])//从右半边寻找小的数
{
j--;
}
a[i] = a[j];
while(i < j && key >= a[i])//从左半边寻找大的数
{
i++;
}
a[j] = a[i];
}
a[i] = key;
sort(a, left, i - 1);
sort(a, i + 1, right);
} 分析:快速排序的时间复杂度取决于对key值的选取,若key值接近待排序数列的中位数,那算法的速度就会比较快;若key值接近待排序数列的最值,那算法的速度就比价慢。时间复杂度最快是o(nlogn),最慢是o(n^2)。
小结:查找算法主要有顺序查找和二分查找等,排序算法主要有选择排序、插入排序、冒泡排序和快速排序等。
8. 第八章 动态规划算法概述与分析
8.1 动态规划算法的基本思想
动态规划算法的基本思想是将待求解问题用不同的状态来表示,通过不同状态间的联系,从子状态出发,求解得到最终状态的答案。不同状态之间的联系称为状态转移方程。
8.2 实例及其分析
开心的金明(洛谷P1060)
实现代码:
#include //头文件
int t[1000001],m[1000001],f[1000001];//t数组是用来表示这个物品的价格(即这个物品的大小),m数组是用来表示这个物品的价值的(即这个物品的权值),f数组是用来存储答案的。
int maxx(int x,int y)//maxx函数是用来判断两个数到底哪一个数大的函数
{
return x>y?x:y;//如果x>y,那么就返回x,否则就返回y
}
int main()//主函数
{
int v=0,n=0;//v表示金明的妈妈给了金明v元钱(即这个背包的大小),n表示金明有n件想买的物品(即有n件物品可以拿来放入背包)。那么,这个问题就可以简化成:有一个背包的大小为v,你可以选择将这n个物品中的几个放入这个背包里,使得这些放入背包的物品的权值最大
scanf("%d %d",&v,&n);//输入v和n(即这个背包的容量和有n件物品可以选择放进这个背包里面)
for(int i=1;i<=n;i++)//读入这n个物品的价格和重要度
{
int x=0;//初始化(x是等一下要读入的第i件物品的重要度,即题目里面的p[i])
scanf("%d %d",&t[i],&x);//读入第i件物品的价格和它的重要度(即题目里面的v[i]和p[i])
m[i]=t[i]*x;//这个物品的价值(因为要求的答案是为不超过总钱数的物品的价格与重要度乘积的总和的最大值,所以将这两个数)相乘
}
for(int i=1;i<=n;i++)//从第1件物品做到第i件物品
{
for(int j=v-t[i];j>=0;j--)//从楼顶做到楼底
{
f[j+t[i]]=maxx(f[j]+m[i],f[j+t[i]]);//更新最大值(即与原来的值和新的值相比较,请想一下为什么要这样做,以及f[0]为什么不用等于1)
}
}
printf("%d",f[v]);//输出最大值(即答案)
return 0;//结束程序
} 分析:这是一道经典的0-1背包问题,特点是每种物品仅有一件,可以选择放或不放,用子问题定义状态:即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是:f[i][v]=max{ f[i-1][v], f[i-1][v-w[i]]+v[i] }。这道题使用里空间优化的手段。
小结:能用动态规划求解的题目,必须具有最优子结构和无后效性的特点。动态规划的程序既可以写成“递归函数+用函数记录计算结果”的形式,也可以写成不用递归,在数组内由已知推未知的递推形式。
9. 第九章 贪心算法概述与分析
9.1 贪心算法的基本思想
贪心算法是指从问题的初始状态出发,通过多次的贪心选择,最终得到整个问题的最优解。即由局部最优,得到全局最优。
9.2 实例及其分析
木棍加工(洛谷p1233)
实现代码:
#include
#include
using namespace std;
struct thing{
int lo,wi;
}t[5005];//木棍定义为结构体
bool comp(thing &a,thing &b){
if(a.lo==b.lo)return a.wi>b.wi;
return a.lo>b.lo;
}//定义比较函数,先按从高到低排列长度,长度相同的按从高到低排列宽度
bool used[5005]={};//是否被处理过
int main(){
ios::sync_with_stdio(false);//取消输入流同步,加快输入速度
int n,sum=0,twi;
cin>>n;
for(int i=1;i<=n;i++){
cin>>t[i].lo;
cin>>t[i].wi;
}//输入
sort(t+1,t+n+1,comp);//排序
for(int i=1;i<=n;i++){//双重循环
if(used[i]==0){//如果这个木棍被处理过就跳过
twi=t[i].wi;//保存现有宽度
for(int j=i+1;j<=n;j++){//向后搜索
if(t[j].wi<=twi&&used[j]==0){//如果有宽度小于现有宽度且没有被处理过
used[j]=1;//处理这个木棍
twi=t[j].wi;//保存这个木棍的宽度
}
}
}
}
for(int i=1;i<=n;i++){
if(used[i]==0)sum++;//如果没用过就加1分钟
}
cout< 先将长度排序,再依次寻找宽度不上升序列,将它们全部标记,最后寻找没有被标记的。
小结:在对问题求解时,贪心算法总是做出在当前看来是最好的选择。
10. 第十章 回溯法概述与分析
10.1 回溯法的基本思想
回溯法是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
10.2 实例及其分析
八皇后(洛谷p1219)
实现代码:
#include
#include
#include
#include
using namespace std;
int a[100],b[100],c[100],d[100];
//a数组表示的是行;
//b数组表示的是列;
//c表示的是左下到右上的对角线;
//d表示的是左上到右下的对角线;
int total;//总数:记录解的总数
int n;//输入的数,即N*N的格子,全局变量,搜索中要用
int print()
{
if(total<=2)//保证只输出前三个解,如果解超出三个就不再输出,但后面的total还需要继续叠加
{
for(int k=1;k<=n;k++)
cout<n)
{
print();//输出函数,自己写的
return;
}
else
{
for(int j=1;j<=n;j++)//尝试可能的位置
{
if((!b[j])&&(!c[i+j])&&(!d[i-j+n]))//如果没有皇后占领,执行以下程序
{
a[i]=j;//标记i排是第j个
b[j]=1;//宣布占领纵列
c[i+j]=1;
d[i-j+n]=1;
//宣布占领两条对角线
queen(i+1);//进一步搜索,下一个皇后
b[j]=0;
c[i+j]=0;
d[i-j+n]=0;
//(回到上一步)清除标记
}
}
}
}
int main()
{
cin>>n;//输入N*N网格,n已在全局中定义
queen(1);//第一个皇后
cout< 分析:本道题最重要的就是记录下皇后占领的格子(打标记的思想),通过此判断下一个皇后是否可以在某个位置,如果可以,则继续搜索下一个皇后可以在的位置,如果不行,则清除标记回到上一步,继续搜索。
小结:以深度优先搜索方式获得问题的解的算法称为回溯法,可用于解组合数大的问题。
11. 第十一章 随机算法概述与分析
11.1 随机算法的基本思想
随机化算法中使用了随机函数,且随机函数的返回值直接或者间接的影响了算法的执行流程或执行结果。随机化算法基于随机方法,依赖于概率大小。
11.2 实例及其分析
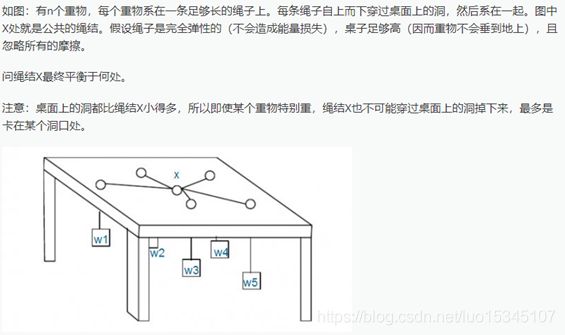
平衡点(洛谷P1337)
分析:本题可以使用模拟退火算法来解决。选定一个初始状态(比如选定所有点坐标的平均数),选定一个初始温度T。当温度大于一个边界值时:
随机变化坐标,变化幅度为 T 。
计算新解与当前解的差 DE。
如果新解比当前解优(DE > 0),就用新解替换当前解。
否则以 exp(DE / T) 的概率用新解替换当前解。
温度乘上一个小于1的系数,即降温。
这样,随着温度不断降低,变化幅度也越来越小,接受一个更劣的解的概率也越来越小。
实现代码:
#include
#include
#include
#include
int Read()
{
int x=0,y=1;
char c=getchar();
while(!isdigit(c))
{
if(c=='-')
{
y=-1;
}
c=getchar();
}
while(isdigit(c))
{
x=(x<<3)+(x<<1)+(c^48);
c=getchar();
}
return x*y;
}
struct Node
{
int x,y,weight;
}node[10005];
int n;
double potential_energy(double nowx,double nowy)
{
double sum=0;
for(int i=1;i<=n;i++)
{
double delx=nowx-node[i].x;
double dely=nowy-node[i].y;
sum+=(sqrt(delx*delx+dely*dely))*node[i].weight;
//物重一定,绳子越短,重物越低,势能越小
//势能又与物重成正比
}
return sum;//在(nowx,nowy)处的总势能
}
double xans,yans;//最终答案
double ans=1e18+7,t;//势能与温度
const double delta=0.993;//降温系数
void simulate_anneal()
{
double xx=xans;//钦定一个初始位置
double yy=yans;
t=1926;//t是温度
while(t>1e-14)
{
double xtemp=xans+(rand()*2-RAND_MAX)*t;
double ytemp=yans+(rand()*2-RAND_MAX)*t;
//随机一个新的坐标,变化幅度为t
//这里要注意rand()和rand()*2-RAND_MAX的区别
//rand()的范围是0~RAND_MAX-1
//rand()*2-RAND_MAX的范围是-RAND_MAX到RAND_MAX-1
double new_ans=potential_energy(xtemp,ytemp);//计算当前解的势能
double DE=new_ans-ans;
if(DE<0)//如果是一个更优解
{
xx=xtemp;
yy=ytemp;//就接受
xans=xx;
yans=yy;
ans=new_ans;
}
else if(exp(-DE/t)*RAND_MAX>rand())//能否接受这个差
{
//更新坐标
xx=xtemp;
yy=ytemp;
}
t*=delta;//降温
}
}
void SA()//跑三次,总有一次是对的
{
simulate_anneal();
simulate_anneal();
simulate_anneal();
}
int main()
{
n=Read();
for(int i=1;i<=n;i++)
{
node[i].x=Read();
node[i].y=Read();
node[i].weight=Read();
}
SA();
printf("%.3lf %.3lf",xans,yans);
return 0;
} 小结:对于一些可能陷入局部最优的算法,如果能与随机化算法相结合,有可能获得较好的结果。
总结:就这样吧~~~