联合概率、边缘概率、条件概率之间的关系&贝叶斯公式
前言
有挺长一段时间没有更新博客了,一方面是学校期末考试,后来又看了一些很基础的编程数学思想的东西(《程序员的数学》第一卷),大多数东西都在之前的学习和使用中都有注意到,所以没有什么特别值得更新的。这次看到了卷2《程序员的数学2——概率统计》发现之前在概率论的学习过程中,忽略了一些比较重要的东西,这边就来记录一下,如果有写的不对和写得不好的地方,请各位看官老爷帮忙指出~
正文
这次主要介绍的是多个随机变量之间的关系,主要涉及联合概率,边缘概率,条件概率这三种关系,还有一个利用他们之间关系导出的非常重要的公式:贝叶斯公式
1.联合概率
联合概率指的是包含多个条件且所有条件同时成立的概率,记作P(X=a,Y=b)或P(a,b),有的书上也习惯记作P(ab),但是这种记法个人不太习惯,所以下文采用以逗号分隔的记法。
一定要注意是所有条件同时成立!
2.边缘概率
边缘概率是与联合概率对应的,P(X=a)或P(Y=b),这类仅与单个随机变量有关的概率称为边缘概率
3.联合概率与边缘概率的关系
P(X=a)=∑bP(X=a,Y=b) P ( X = a ) = ∑ b P ( X = a , Y = b )
P(Y=b)=∑aP(X=a,Y=b) P ( Y = b ) = ∑ a P ( X = a , Y = b )
求和符号表示穷举所有Y(或X)所能取得b(或a)后,所有对应值相加得到的和
4.条件概率
条件概率表示在条件Y=b成立的情况下,X=a的概率,记作P(X=a|Y=b)或P(a|b),它具有如下性质:
“在条件Y=b下X的条件分布”也是一种“X的概率分布”,因此穷举X的可取值之后,所有这些值对应的概率之和为1即:
∑aP(X=a|Y=b)=1 ∑ a P ( X = a | Y = b ) = 1
5.联合概率、边缘概率与条件概率之间的关系
P(X=a|Y=b)=P(X=a,Y=b)P(Y=b) P ( X = a | Y = b ) = P ( X = a , Y = b ) P ( Y = b )
为了方便理解这个式子,可以将概率转化为面积:
- 联合概率P(X=a,Y=b)
满足X=a且Y=b的面积- 边缘概率P(X=a)
不考虑Y的取值,所有满足X=a的区域的总面积- 条件概率P(X=a|Y=b)
在Y=b的前提下,满足X=a的面积(比例)
通过以上示例,稍加计算这三种概率之间的关系便可一目了然
6.条件联合分布的分解
我们可以根据具体情况,像下面这样灵活的分解条件联合分布
P(X=a,Y=b|Z=c)=P(X=a|Y=b,Z=c)P(Y=b|Z=c) P ( X = a , Y = b | Z = c ) = P ( X = a | Y = b , Z = c ) P ( Y = b | Z = c )
这只是一个例子,作为启发,类似的分解方法可以根据实际情况不同而进行不同的分解。为了大家可以有效掌握这种方法,建议自己从式子左侧根据上面三种概率的关系式进行一遍推导。
再给大家留一个看起来非常复杂的式子,大家可以自己试试看能否从左侧推导至右侧
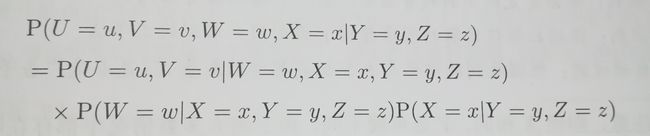
7.贝叶斯公式
说了那么多,终于到大boss了,贝叶斯公式!但是,先别急,需要先引入两个概念
- 先验概率:知道原因推结果的,P(原因)、P(结果|原因)等
- 后验概率:根据结果推原因的,P(原因|结果)等
贝叶斯公式解决的是一些原因X无法直接观测、测量,而我们希望通过其结果Y来反推出原因X的问题,也就是知道一部分先验概率,来求后验概率的问题。
举个栗子:
打到怪物就能获得宝箱,但是宝箱有2/3的概率是陷阱,玩家可以通过魔法来检查,但是有1/4的误判概率,问:假设玩家利用魔法判定此宝箱没有陷阱,求宝箱有陷阱的概率
我们已知的先验概率有
P(有陷阱)=2/3;P(没有发现|有陷阱)=1/4;P(发现了|没有陷阱)=1/4
要求的后验概率为
P(有陷阱|没有发现)
我们依旧使用面积来帮助我们解题,根据已知划分出的面积情况如下图所示
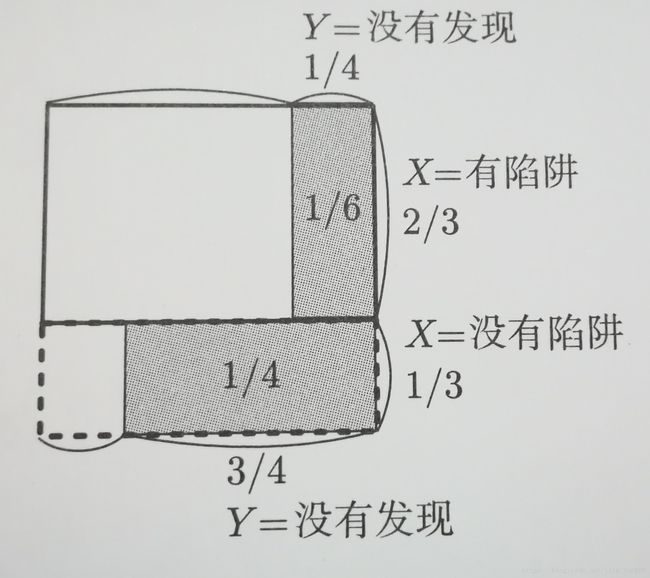
我们可以推得:
P(有陷阱|没有发现)=P(有陷阱,没有发现)P(没有发现) P ( 有 陷 阱 | 没 有 发 现 ) = P ( 有 陷 阱 , 没 有 发 现 ) P ( 没 有 发 现 )
P(没有发现)=P(没有发现|有陷阱)P(有陷阱)+P(没有发现|没有陷阱)P(没有陷阱) P ( 没 有 发 现 ) = P ( 没 有 发 现 | 有 陷 阱 ) P ( 有 陷 阱 ) + P ( 没 有 发 现 | 没 有 陷 阱 ) P ( 没 有 陷 阱 )
联立两式我们就可以得到一个由已知条件求P(有陷阱|没有发现)的式子
P(有陷阱|没有发现)=P(有陷阱,没有发现)P(没有发现|有陷阱)P(有陷阱)+P(没有发现|没有陷阱)P(没有陷阱) P ( 有 陷 阱 | 没 有 发 现 ) = P ( 有 陷 阱 , 没 有 发 现 ) P ( 没 有 发 现 | 有 陷 阱 ) P ( 有 陷 阱 ) + P ( 没 有 发 现 | 没 有 陷 阱 ) P ( 没 有 陷 阱 )
这就是对应于此题的贝叶斯公式。它的的一般形式如下:
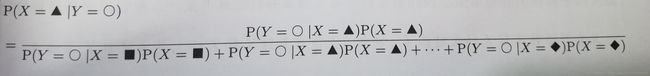
其中“…”的部分需要列出X所有可能的值,并求和。
在记忆贝叶斯公式时,很容易搞错竖线左右两侧的值,因此建议大家在习惯使用贝叶斯公式时,最好先根据定义与性质当场推导,而不要仅仅凭记忆默写。

后记
这次的内容虽然很基础,但是对于条件联合分布分解和贝叶斯公式适用的问题类型这里,在我之前的学习中的确不扎实,做个总结梳理一下自己的思路,也希望能给跟我有同样问题的朋友提供一些帮助。
