DFS序与欧拉序的区别

DFS序与欧拉序的区别

dfs序：是指将一棵树被dfs时所经过的节点顺序（不绕回原点）。
欧拉序：就是从根结点出发，按dfs的顺序在绕回原点所经过所有点的顺序。

作用

通过dfs序判断v节点的时间区间是否在u节点的时间区间内。
通过欧拉序求u和v的最近公共祖先。

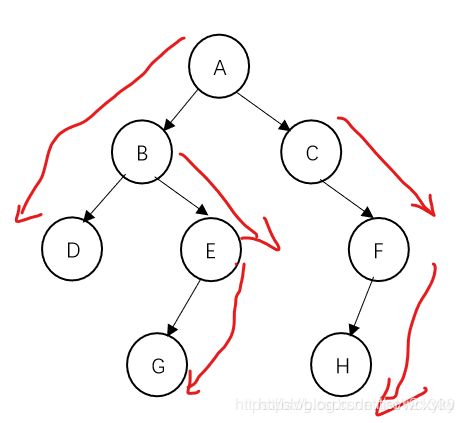
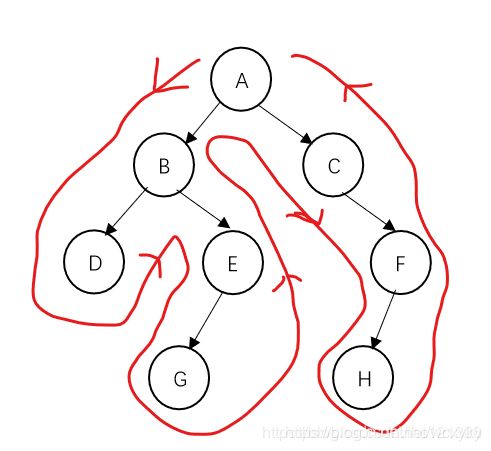
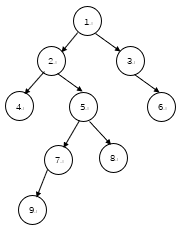
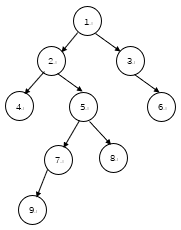
用图说话

dfs序：A-B-D-E-G-C-F-H

欧拉序：A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A

 

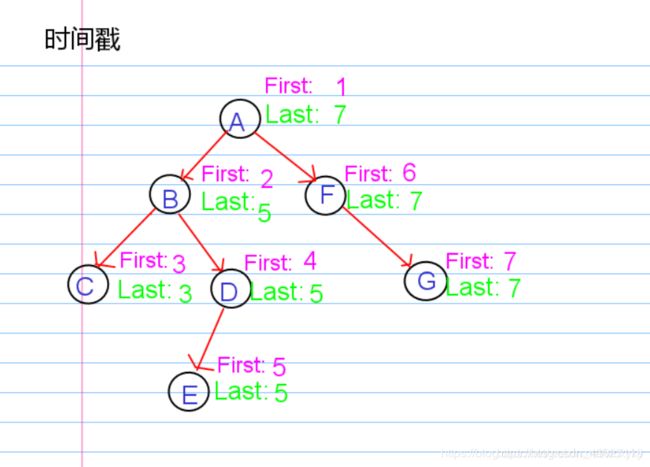
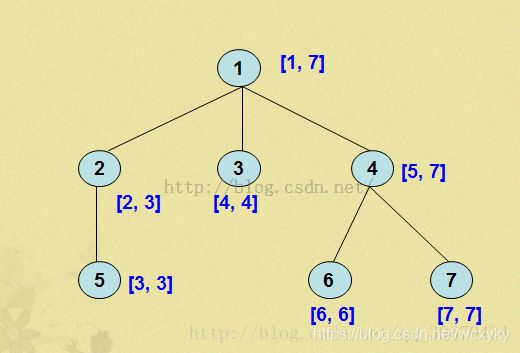
时间戳

 

时间戳我们有两个标记，第一个是第一次访问的时候记录一下，然后是在最后一次访问时再标记一下。 

时间戳的性质：我们可以直接通过时间戳来判断一个节点是否是另一个节点的子节点。时间戳之后，那么树的每个节点就具有了区间的性质。 

 

DFS序

DFS序核心代码

const int maxn = 1e5+5;
vector g[maxn]; //存放节点
int s[maxn], e[maxn];//s[maxn]存放“入时间戳”，e[maxn]存放“出时间戳”；
int n,id,len;
int dfsxu[20000];//存放dfs序

void dfs(int u, int fa) {
	s[u] = ++id;
	dfsxu[++len]=u;
	for(int i = 0; i < g[u].size(); ++i) {
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v, u);
	}
	e[u] = id;
}

 DFS序完整代码

#include 
using namespace std;
const int maxn = 1e5+5;
vector g[maxn]; //存放节点
int s[maxn], e[maxn];//s[maxn]存放“入时间戳”，e[maxn]存放“出时间戳”；
int n,id,len;
int dfsxu[20000];//存放dfs序

void dfs(int u, int fa) {
	s[u] = ++id;
	dfsxu[++len]=u;
	for(int i = 0; i < g[u].size(); ++i) {
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v, u);
	}
	e[u] = id;
}
int main() {
    memset(s,0,sizeof(s));
    memset(e,0,sizeof(e));
    memset(dfsxu,0,sizeof(dfsxu));
	ios::sync_with_stdio(0);
	cin >> n;
	for(int i = 1; i < n; ++i) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	id = 0;
	dfs(1, -1);
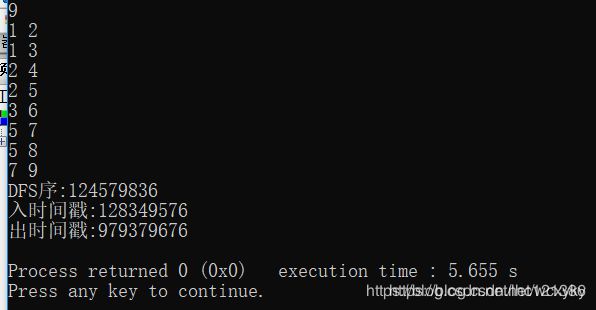
    cout<<"DFS序:";
    for(int i=1;s[i]!=0;i++)
    {
        cout<

运行结果：

通过dfs序判断v节点的时间区间是否在u节点的时间区间内

#include 
using namespace std;
const int maxn = 1e5+5;
vector g[maxn];
int s[maxn], e[maxn];
int n, q, id;
void dfs(int u, int fa) {
	s[u] = ++id;
	for(int i = 0; i < g[u].size(); ++i) {
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v, u);
	}
	e[u] = id;
}
int main() {
	ios::sync_with_stdio(0);
	cin >> n >> q;
	for(int i = 1; i < n; ++i) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	id = 0;
	dfs(1, -1);
	for(int i = 1; i <= q; ++i) {
		int u, v;
		cin >> u >> v;
		if(s[u] <= s[v] && e[v] <= e[u]) {
			cout << "YES" << endl;
		}
		else {
			cout << "NO" << endl;
		}
	}
	return 0;
}

 

欧拉序

核心代码：

vector g[40010]; //存放节点
int oulaxu[80020]; //存放欧拉序在，在欧拉序中第一次出现为“入时间戳”，第二次出现为“出时间戳”。
int len;

void dfs(int u,int fa)
{
    oulaxu[++len]=u;
    int sz=g[u].size();
    for(int i=0; i

完整代码：

#include
#include
#include
#include
#include
#include
using namespace std;

vector g[40010]; //存放节点
int oulaxu[80020]; //存放欧拉序在，在欧拉序中第一次出现为“入时间戳”，第二次出现为“出时间戳”。
int len;

void dfs(int u,int fa)
{
    oulaxu[++len]=u;
    int sz=g[u].size();
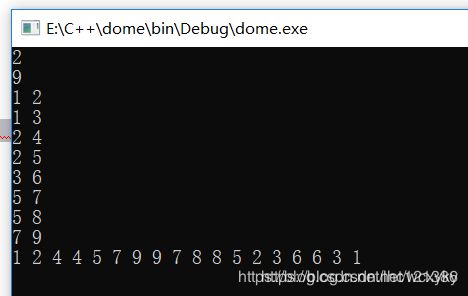
    for(int i=0; i

 运行结果

通过欧拉序求u和v的最近公共祖先 

#include 
using namespace std;
const int maxn = 1e5+5;
vector g[maxn];
int E[maxn*2], R[maxn], dep[maxn];
int f[maxn*2][20];
int n, q, cnt;
void dfs(int u, int fa, int deps) {
	E[++cnt] = u;
	R[u] = cnt;
	dep[u] = deps;
	for(int i = 0; i < g[u].size(); ++i) {
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v, u, deps+1);
		E[++cnt] = u;
	}
}
void rmq_init() {
	for(int i = 1; i <= cnt; ++i) {
		f[i][0] = E[i];
	}
	for(int j = 1; (1<> n >> q;
	for(int i = 1; i < n; ++i) {
		int u, v;
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	cnt = 0;
	dfs(1, -1, 1);
	rmq_init();
	for(int i = 1; i <= q; ++i) {
		int u, v;
		cin >> u >> v;
		cout<