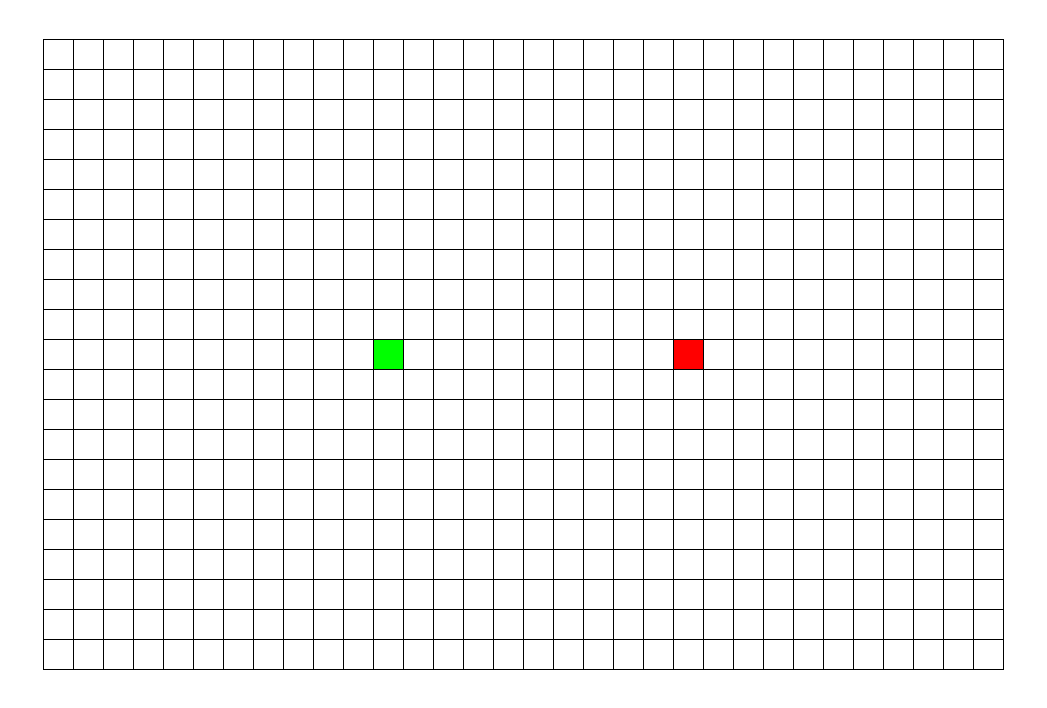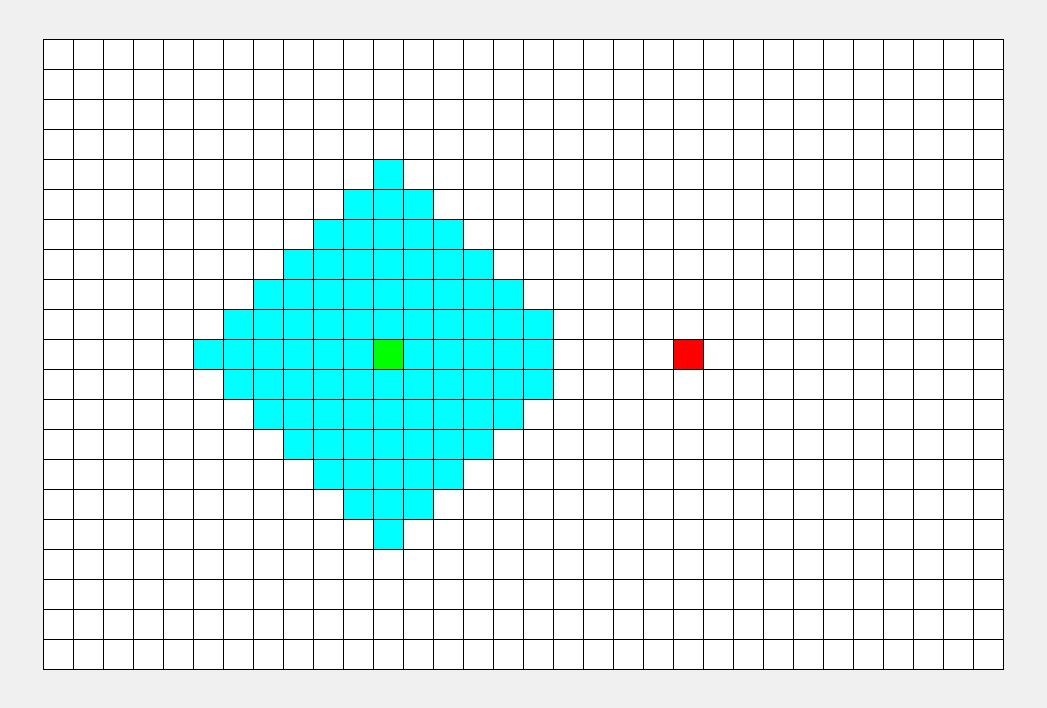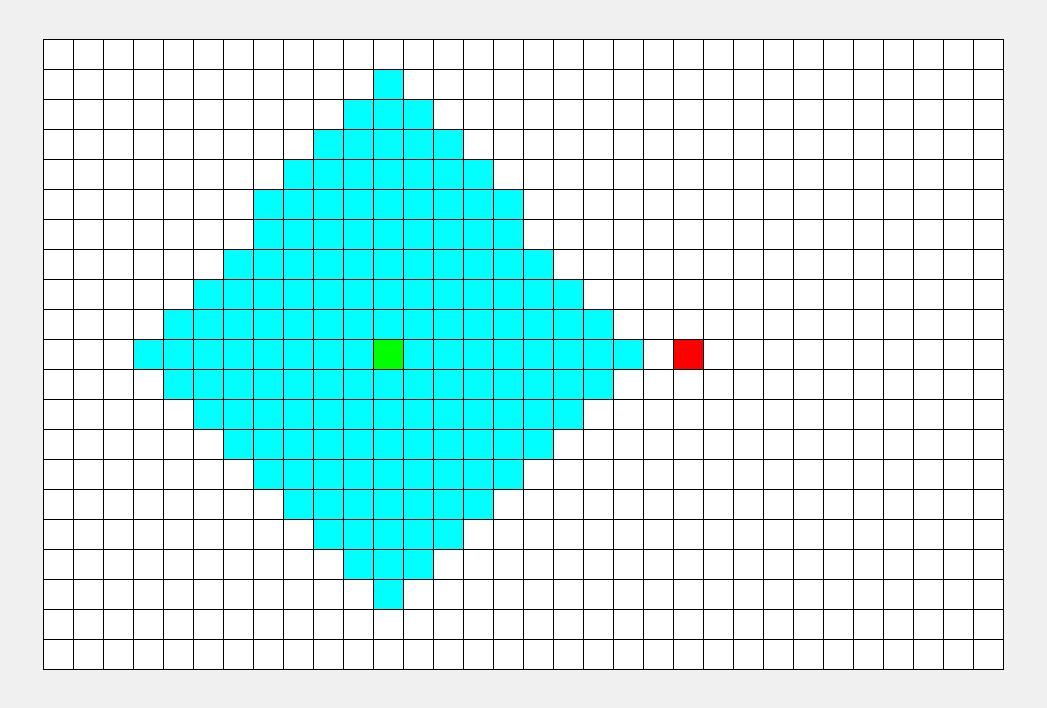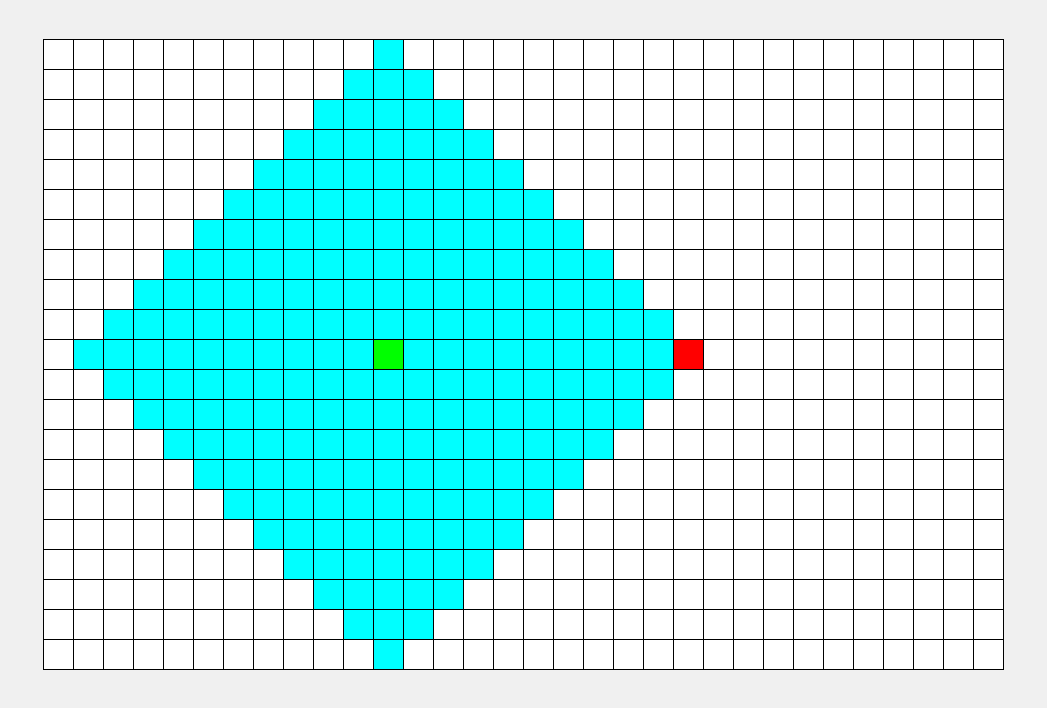
BFS和DFS

1.DFS（深度优先搜索）

2.BFS（宽度/广度优先搜索）

区别

	实现方法	基本思想	解决问题	N规模
DFS	栈/递归	回溯法，一次访问一条路，到达终点返回	所有解问题，连通性问题	浪费时间节省空间，N <= 200
BFS	队列	分治限界法，一次访问多条路，每一层存储大量信息	最优解问题（最短路）	浪费空间节省时间，N <= 1000

总结：dfs()到达递归终止条件即返回，否则继续递归；bfs()首先创建一个队列，然后把队首元素压入队列，再把下一层逐个元素送入队列。

DFS(dep,...) dep表示当前DFS的深度{
    if(找到解 || 走不下去了) {
        ...;
        return ;
    }
    枚举下一种情况， DFS(dep + 1, ...)
}

BFS
通常用队列来实现
初始化队列Q
Q = {起点S}; 标记S为已访问；
while(!Q.empty()) {
    取Q队首元素U； 
    U出队；
    if(U == 目标状态) {...}
    所有与U相邻且未被访问的点入队列；
    标记U为已访问；
}

https://blog.csdn.net/henu111/article/details/81163136?utm_source=app

（1）

一天蒜头君掉进了一个迷官里面，蒜头君想逃出去，可怜的蒜头君连迷官是否有能逃出去的路都不知道。看在蒜头君这么可怜的份上,就请聪明的你告诉蒜头君是否有可以逃出去的路。

输入格式：

第一行输入两个整数n和m,表示这是一个n X m的迷宫。
接下来的输入一个n行m列的迷宫。其中’S’ 表示蒜头君的位置’*’ 表示墙,蒜头君无法通过，’. ‘表示路,蒜头君可以通过’.'移动，‘T’ 示迷宫的出口(蒜头君每次只能移动到四个与他相邻的位置一上， 下, 左，右)。

输出格式：
输出一个字符串，如果蒜头君可以逃出迷宫输出"yes"，否则输出"no"。
 

输入样例1：
3 4
S**.
..*.
***T

输出样例1：
no

输入样例2：
3 4
S**.
....
***T

输出样例1：
yes

深度优先所搜dfs：

#include 
using namespace std;
int n, m;
bool vis[15][15];
char s[15][15];
int dir[4][2] = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
bool flag;
bool in(int x, int y)
{
	return 0 <= x && x < m && 0 <= y && y < n;
}
void dfs(int x, int y)
{
	if (s[x][y] == 'T')
	{
		flag = 1;
		return;
	}
	vis[x][y] = 1;
	for (int i = 0; i < 4; i++)
	{
		int tx = x + dir[i][0];
		int ty = y + dir[i][1];
		if (!vis[tx][ty] && in(tx, ty) && s[x][y] != '*')
		{
			dfs(tx, ty);
		}
	}
}
int main()
{
	cin >> m >> n;
	for (int i = 0; i < m; i++)
	{
		scanf("%s", s[i]);
	}
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (s[i][j] == 'S')
			{
				dfs(i, j);
				break;
			}
		} 
	}
	if (flag)
	{
		cout << "yes" << endl;
	}
	else
	{
		cout << "no" << endl;
	}
	return 0;
}

 

广度优先搜索（bfs）:

#include 
#include 
using namespace std;
//使用结构体传递变量的值，相当于dfs中形参传递变量的值 
struct node {
    int x, y;
    node(int xx, int yy)
    {
        x = xx;
        y = yy;
    }
};
int dir[4][2] = {{1, 0}, {-1, 0}, {0, -1}, {0, 1}};
char s[15][15];
bool vis[15][15];
bool flag;
int n, m;
bool in(int x, int y)
{
	return 0 <= x && x < m && 0 <= y && y < n;
}
void bfs(int sx, int sy)
{
	queue q;
	q.push(node(sx, sy));//以上两行充当dfs形参传递x, y变量的值 
	vis[sx][sy] = 1;
	while (!q.empty())
	{
		node now = q.front();
		q.pop();//访问当前位置并删除 
		for (int i = 0; i < 4; i++)//向四个方向搜索 
		{
			int tx = now.x + dir[i][0];
            int ty = now.y + dir[i][1];
            if (in(tx, ty) && s[tx][ty] != '*' && !vis[tx][ty])//满足条件 
            {
            	if (s[tx][ty] == 'T')//到达终点 
				{
					flag = 1;
					return;
				}
				else
				{
					vis[tx][ty] = 1;//标记下一个位置 
					q.push(node(tx, ty));//充当dfs的形参传值，下一次循环相当于dfs的递归调用 
				}
			}
		}
	}
}
int main()
{
	cin >> m >> n;
	for (int i = 0; i < m; i++)
	{
		scanf("%s", s[i]);
	}
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < n; j++)
		{
			if (s[i][j] == 'S')
			{
				bfs(i, j);
				break;
			}
		} 
	}
	if (flag)
	{
		cout << "yes" << endl;
	}
	else
	{
		cout << "no" << endl;
	}
	return 0;
}

PAT 1004

题目描述：给你一个家谱，找到没有孩子的人。换言之，该题用来统计树结构中的叶子结点，可以采用深度优先遍历算法来进行统计。
　　我们采用vector数组作为树的存储结构，std提供了较为强大的函数方便使用。将树结点逐一输入到vector 中，每一个元素存储了该结点的子孩子信息，自动向下探索子孩子，直到vector[i].size()==0表明该结点的子孩子为零，即叶子结点。
　　可以采用循环结构来进行上述遍历，访问每一个结点，也可以使用递归结构。同时，每往下探测一层，需要一个变量来统计所在的层次数，以便统计每层的叶子结点个数。
 

输入：
2 1
01 1 02

输出：
0 1

1.dfs 思路

#include
#include
#include
using namespace std;

vector v[100]; //节点数 
int res[100];       //每层叶子节点数 
int maxdepth = -1;  //最大深度 

void dfs(int node, int depth) {
	if(v[node].size() == 0) {      //搜索到叶子节点，退出保存 
		res[depth]++;              //统计该层的叶子节点 
		maxdepth = max(maxdepth, depth);     //更新最大层数 
		return ;
	}
	for(int i = 0; i < v[node].size(); i++)     //递归调用 
		dfs(v[node][i], depth + 1);
} 
int main() {
	int n, m;
	int node, k;
	cin >> n >> m;
	for(int i = 0; i < m; i++) {
		cin >> node >> k;
		for(int j = 0; j < k; j++) {
			int temp;
			cin >> temp;
			v[node].push_back(temp);
		}
	}
	dfs(1, 0);   //(节点， 该节点所在层) 
	cout << res[0];
	for(int i = 1; i <= maxdepth; i++)
	cout << " " << res[i];
	cout << endl;
	return 0;
}

2. bfs 思路

#include
#include
#include
#include
using namespace std;
vector v[100];       //节点向量 
int maxdepth = -1;        //最大层数 
int res[100];             //每层的叶子节点数量 
int level[100];           //记录该节点所在层数 、、区别于bfs 
void bfs() {
	queue q;        //定义一个队列 
	q.push(1);           //根节点入列 
	level[1] = 0;        //根节点所在层为0 
	while(!q.empty()) {   //访问该节点下的所有元素 
		int node = q.front();   //获取队首元素 
		q.pop();
		maxdepth = max(maxdepth, level[node]);
		if(v[node].size() == 0) res[level[node]]++;
		for(int i = 0; i < v[node].size(); i++) {
			q.push(v[node][i]);     //子节点入列 
			level[v[node][i]] = level[node] + 1;     //同时记录该子节点所在的层次 
		}
	}
}
int main(){
	int n, m;
	cin >> n >> m;
	int node, k;
	for(int i = 0; i < m; i++) {
		cin >> node >> k;
		for(int j = 0; j < k; j++) {
			int temp;
			cin >> temp;
			v[node].push_back(temp);
		}
	}
	bfs();
	cout << res[0];
	for(int i = 1; i <= maxdepth; i++)
	cout << " " << res[i];
	cout << endl;
	return 0;
} 

PAT 1090

 

A supply chain is a network of retailers（零售商）, distributors（经销商）, and suppliers（供应商）-- everyone involved in moving a product from supplier to customer.

Starting from one root supplier, everyone on the chain buys products from one's supplier in a price P and sell or distribute them in a price that is r% higher than P. It is assumed that each member in the supply chain has exactly one supplier except the root supplier, and there is no supply cycle.

Now given a supply chain, you are supposed to tell the highest price we can expect from some retailers.

Input Specification:
Each input file contains one test case. For each case, The first line contains three positive numbers: N (≤100000), the total number of the members in the supply chain (and hence they are numbered from 0 to N−1); P, the price given by the root supplier; and r, the percentage rate of price increment for each distributor or retailer. Then the next line contains N numbers, each number S​i is the index of the supplier for the i-th member. S ​root for the root supplier is defined to be −1. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print in one line the highest price we can expect from some retailers, accurate up to 2 decimal places, and the number of retailers that sell at the highest price. There must be one space between the two numbers. It is guaranteed that the price will not exceed 10
​10
​​ .

Sample Input:
9 1.80 1.00
1 5 4 4 -1 4 5 3 6

Sample Output:
1.85 2

1.dfs 解法

#include
#include
#include 
#include
using namespace std;
vector v[10001];
int maxdepth = -1, maxnum = 0;
void bfs(int index, int depth) {
	if(v[index].size() == 0) {
		if(depth == maxdepth) maxnum++;
		if(depth > maxdepth) {
			maxdepth = depth;
			maxnum = 1;
		} 
	}
	for(int i = 0; i < v[index].size(); i++)
		bfs(v[index][i], depth + 1);
}
int main(){
	int n, root;
	double p, r;
	cin >> n >> p >> r;
	for(int i = 0; i < n; i++) {
		int temp;
		cin >> temp;
		if(temp == -1)
		root = i;
		else v[temp].push_back(i);
	}
	bfs(root, 0);
	printf("%.2f %d\n", p * pow(1.0 + r / 100 , maxdepth), maxnum);
	return 0;
} 

2.bfs解法

#include
#include
#include 
#include
#include
using namespace std;
vector v[100001];
int level[100001];
int maxdepth = -1, maxnum = 0;
void bfs(int node) {
	queue q;
	q.push(node);
	level[node] = 0;
	while(!q.empty()) {
		int index = q.front();
		q.pop();
		if(v[index].size() == 0) {
			if(maxdepth == level[index]) maxnum++;
			if(maxdepth < level[index]) {
				maxdepth = level[index];
				maxnum = 1;
			} 
		}
		for(int i = 0; i < v[index].size(); i++) {
			q.push(v[index][i]);
			level[v[index][i]] = level[index] + 1;
		}	
	}
}
int main(){
	int n, root;
	double p, r;
	cin >> n >> p >> r;
	for(int i = 0; i < n; i++) {
		int temp;
		cin >> temp;
		if(temp == -1)
		root = i;
		else v[temp].push_back(i);
	}
	bfs(root);
	printf("%.2f %d\n", p * pow(1.0 + r / 100 , maxdepth), maxnum);
	return 0;
} 

PAT 1091 三维问题

Sample Input:
3 4 5 2
1 1 1 1
1 1 1 1
1 1 1 1
0 0 1 1
0 0 1 1
0 0 1 1
1 0 1 1
0 1 0 0
0 0 0 0
1 0 1 1
0 0 0 0
0 0 0 0
0 0 0 1
0 0 0 1
1 0 0 0


Sample Output:
26

BFS解题思路: 连通性的问题

#include
#include
#include
using namespace std;
int arr[1300][130][80];
bool visit[1300][130][80];
int m, n, l, t;
struct node{
	int x, y, z;
};
bool isValid(int x, int y, int z) {
    if(x < 0 || x >= m || y < 0 || y >= n || z < 0 || z >= l) return false;
    if(arr[x][y][z] == 0 || visit[x][y][z] == true) return false;
    return true;
}
int dir[6][3] = {{1, 0, 0}, {-1, 0, 0}, {0, 1, 0}, {0, -1, 0}, {0, 0, 1}, {0, 0, -1}};
int bfs(int x, int y, int z) {
	int sum = 0;
	node temp;
	temp.x = x; temp.y = y; temp.z = z;
	queue q;
	q.push(temp);
	visit[x][y][z] = true;
	while(!q.empty()) {
		node d = q.front();
		q.pop();
		sum++;
		
		for(int h = 0; h < 6; h++) {    //循环中不能改变d.x， d.y , d.z的值 
			int tx = d.x + dir[h][0];
			int ty = d.y + dir[h][1];
			int tz = d.z + dir[h][2];
			if(isValid(tx, ty, tz)){
				visit[tx][ty][tz] = true;
				q.push({tx, ty, tz});
			}
		}
	}
	if(sum >= t) {
		//cout << sum << endl; 
		return sum;
	}
	else 
	   return 0;
}
int main() {
	//freopen("1091.txt", "r", stdin);
    scanf("%d %d %d %d", &m, &n, &l, &t);
    for(int i = 0; i < l; i++)
        for(int j = 0; j < m; j++)
            for(int k = 0; k < n; k++)
                scanf("%d", &arr[j][k][i]);
    int ans = 0;
    for(int i = 0; i < l; i++) {
        for(int j = 0; j < m; j++) {
            for(int k = 0; k < n; k++) {
                if(arr[j][k][i] == 1 && visit[j][k][i] == false)
                    ans += bfs(j, k, i);
            }
        }
    }
    printf("%d", ans);
    return 0;
}

 

 

PAT 1103  dfs(偏难）

 

Sample Input 1:
169 5 2

Sample Output 1:
169 = 6^2 + 6^2 + 6^2 + 6^2 + 5^2

Sample Input 2:
169 167 3

Sample Output 2:
Impossible

#include
#include
#include
#include
using namespace std;
int n, k, p, maxFacSum = -1;  //maxFacSum记录最大底数之和
vector fac, ans, temp;   // fac可选底数序列，i*i <= n。ans存放最优底数序列，temp存放临时底数系列
void init(){
	int temp = 0, index = 1;
	while(temp <= n) {
		fac.push_back(temp);
		temp = pow(index, p);
		index++;
	}
}
//dfs(),当前访问fac[index],nowK为当前选中的个数
//sum为当前选中的数之和，facSum为当前选中的底数之和 
void dfs(int index, int nowK, int sum, int facSum) {
	if(sum == n && nowK == k) {       //找到一个满足的序列 
		if(facSum > maxFacSum) {       //底数之和更优（dfs一次直接遍历到终点，所以遍历结束时可以直接比较） 
			ans = temp;                //更新最优底数序列 
			maxFacSum = facSum;        //更新最大底数之和 
		}
		return ;
	}
	if(sum > n || nowK > k) return ;   //这种情况下不会产生答案，直接返回 
	if(index >= 1) {                    //fac[0]不需要选择 
		temp.push_back(index);           //把底数index加入临时序列temp
		dfs(index, nowK + 1, sum + fac[index], facSum + index);      //"选"的分支，选index进行遍历 
		temp.pop_back();                 //选的分支结束后把刚加进去的数pop掉
		dfs(index - 1, nowK, sum, facSum);       //"不选"的分支 （此次dfs遍历不选择index） 
	}
}
int main() {
	cin >> n >> k >> p;
	init();    //初始化fac数组 
	dfs(fac.size() - 1, 0, 0, 0);   //从fac的最后一位开始往前搜索
	if(maxFacSum == -1) cout << "Impossible" << endl;
	else {
		cout << n << " = " << ans[0] << "^" << p;
		for(int i = 1; i < ans.size(); i++)
		cout << " + " << ans[i] << "^" << p;
	} 
	return 0;
}