大整数运算包的实现(Java)(2) --快速幂取模、最大公约数、乘法逆元、素数判定、生成大素数
目录
- 一、快速幂取模
- 二、最大公约数(欧几里得算法)
- 三、乘法逆元(扩展欧几里得算法)
- 四、素数判定(米勒罗宾算法)
- 五、生成大素数
- 六、源码下载
上一篇博客 大整数运算包的实现(Java)(1) --加、减、乘、除、模取余、模加(考虑负数),我们实现了基本的大数加、减、乘、除、取余。这篇博客将基于它们实现大数的快速幂取模、最大公约数、乘法逆元、素数判定以及大素数的生成。
一、快速幂取模
假如我们要计算 2100 mod 19,最简单的做法是做99次乘法再模上19。
但这样会有两个问题,1、一直做乘法会很消耗时间;2、数最终会变得很大而难以存储
所以我们会使用快速幂取模(类似二元法),这样我们算7次就可以了。

其中我们还会用到下面两个公式,这样我们得到的数就不至于非常大。

/**
* 快速幂取模
* @param one 底数
* @param two 指数
* @param mod 模
* @return 结果
*/
public static String Power(String one,String two,String mod) {
if(two.equals("0")) { //0次幂结果为1
//System.out.println("Power result=1");
return "1";
}else if(two.equals("1")){ //1次幂结果为它本身
return Mod(one, mod);
}
String count=two,result="1",temp=one;
while(!count.equals("0")){
if(Mod(count, "2").equals("1")) //看它二进制最后一位是不是1
result=Multiply(result, temp, mod);
if(!count.equals("1")) //这里避免最后一次做没用的乘法
temp=Multiply(temp, temp, mod);
count=Division(count, "2"); //次数减1,相当于二进制右移一位
}
//System.out.println(result);
return result;
}
运行结果:
25 mod 7 = 4
210 mod 13 = 10
2100 mod 19 = 17
21000 mod 1777 = 1775
210000 mod 49999 = 100
2100000 mod 998111 = 802658
二、最大公约数(欧几里得算法)
求最大公约数可以使用欧几里得算法,又称辗转相除法。
现在求 52 和 36 的最大公约数:
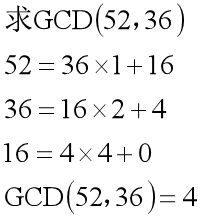
当余数为 0 时,当前算式的除数就是最大公约数。
/**
* 最大公约数
* @param one
* @param two
* @return 结果
*/
public static String GCD(String one,String two) {
if(one.equals(two)) { //相等则GCD=任意一个
//System.out.println("GCD="+one);
return one;
}
int length1=one.length();
int length2=two.length();
String first=null,second=null,temp=null;
if(length1>length2) { //保证第一个数大于第二个,当然也可以不用这么做
first=one;
second=two;
}else if(length1<length2) {
first=two;
second=one;
}else {
for (int i = 0; i < length1; i++) {
if(one.charAt(i)>two.charAt(i)) {
first=one;
second=two;
break;
}
else if(one.charAt(i)<two.charAt(i)) {
first=two;
second=one;
break;
}
}
}
while(!second.equals("0")) {
temp=Mod(first, second);
first=second;
second=temp;
}
//System.out.println("GCD="+first);
return first;
}
三、乘法逆元(扩展欧几里得算法)
如果 ab≡1 mod p,且GCD(a,p)=1(a与p互素),则称a关于模p的乘法逆元为b。
现在使用扩展欧几里得算法来求一下 15 关于模 41 的乘法逆元:

/**
* 扩展欧几里得算法
*/
static String x= "0",y= "0";
public static String ExtendGCD(String a,String b) {
if(b.equals("0")) {
Operation.x="1";
Operation.y="0";
return a;
}
String d=ExtendGCD(b, Mod(a, b));
String temp=Operation.x;
Operation.x=Operation.y;
Operation.y=Subtract(temp, Multiply(Division(a, b), Operation.y));
//System.out.println(" "+Operation.x);
//System.out.println(" "+Operation.y);
return d;
}
/**
* 乘法逆
* @param a
* @param mod
* @return
*/
public static String MultiplicativeInverse(String a,String mod) {
String d=ExtendGCD(a,mod);
if(d.equals("1"))
return Add(Mod(Operation.x, mod), mod, mod);
return "-1"; //没有逆元
}
运行结果:
5模23的乘法逆元=14
28模75的乘法逆元=67
83模108的乘法逆元=95
119模4399的乘法逆元=1109
49999模1234567的乘法逆元=1078243
四、素数判定(米勒罗宾算法)
米勒罗宾算法描述:

判断一个数是不是素数的算法大致如下:


这里要说一下,算法中的幂模算法如果选的不恰当,整个米勒罗宾算法所耗的时间会非常恐怖……
/**
* 米勒罗宾算法
* @param one
* @return
*/
public static boolean MillerRabin(String one) {
if(one.equals("0")||one.equals("1")) //0和1不是素数
return false;
if(one.equals("2")) //2是素数
return true;
if((one.charAt(one.length()-1)-48)%2==0) //偶数不是素数
return false;
String number=Subtract(one, "1"); //计算n-1
String number1=number;
int count=0;
while((number1.charAt(number1.length()-1)-48)%2==0) { //n-1=m*2^t
number1=Division(number1, "2");
count++;
}
for(int i=1;i<=5;i++) { //(a^(n-1))%n=(a^(m*2^t))%n
String random=String.valueOf(i+2);
String x=Power(random, number, one); //(a^m)%n
String y="";
for(int j=1;j<=count;j++) { //((a^m)^(2^t))%n
y=Multiply(x, x, one);
if(y.equals("1")&&!x.equals("1")&&!x.equals(number)) //如果不满足二次探测定理,则不是素数
return false;
x=y;
}
if(!y.equals("1")) //如果不满足费马小定理,则不是素数
return false;
}
return true;
}
运算结果:
111561511是合数
564765326677是素数
49841516591656517是合数
555469971929450687843是素数
262314699260834231863164359738235486290658375509是素数
892209251968203592191654785870096688160362184103664355853918147486564850331是素数
五、生成大素数
/**
* 生成素数算法
* @return 素数
*/
public static String PrimeGeneration() {
//一般来说,整除100以内的所有素数可排除76%不是素数的可能性,整除256以内的所有素数可排除80%
//不是素数的可能性,所以创建小素数表,可以大幅加快速度,当然这个表可以手动生成
String[] table= {"3","7","11","13","17","19","23","29","31","37","41","43","47",
"53","59","61","67","71","73","79","83","89","97","101","103","107","109",
"113","127","131","137","139","149","151","157","163","167","173","179",
"181","191","193","197","199","211","223","227","229","233","239","241",
"251","257","263","269","271","277","281","283","293","307","311","313",
"317","331","337","347","349","353","359","367","373","379","383","389",
"397","401","409","419","421","431","433","439","443","449","457",
"461","463","467","479","487","491","499"};
Random random=new Random();
int flag;
long time1=System.currentTimeMillis();
while(true) {
String number="";
for(int i=1;i<=33;i++) //生成一个随机的大奇数,这个位数任意取
number+=String.valueOf(random.nextInt(899999998)+100000001);
System.out.println(number);
int num=random.nextInt(800)+101; //后三位
if(num%2==0) //跳过偶数
num++;
for(int i=1;i<=50;i++,num+=2) { //搜索附近的50个奇数
String temp="";
if(num%5==0) //跳过5的倍数
num+=2;
temp=temp+number+String.valueOf(num);
flag=0;
for(int j=0;j<table.length;j++) {
if(Mod(temp, table[j]).equals("0")) { //看能不能被小整数整除
flag=1;
break;
}
}
if(flag==1)
continue;
else
if(MillerRabin(temp)) { //米勒罗宾算法
System.out.println("素数: "+temp);
System.out.println("时间差="+(System.currentTimeMillis()-time1)+"ms");
return temp;
}
}
}
}
运行结果(生成300位十进制大素数):
955042930633410289133616296687431777269353980956568253574985061454859846383784618868936295454149058329055354262839296541908590329891268218404276396709186373481902442299599349413886590143757678944807286223232776732690994758060943148907454012806238319657554857310557054678934303822406793932126613431907是素数
时间差=369529ms
886561163228838664750509032768759020351470065461506216295171421466522603290150530199373404129571069480539452635354057998985307892246327624821492158196842621382357442511837684610582698182410676560942977011624164506742932167839443913503332061016760221262755081522835308001246894308971214499396769460513是素数
时间差=29439ms
214870052980815367577291784627902708719802277128149369356311939236596853366271103968812931332145864571367016263259506949201985903708991330657005820918132219051420306215369688007649436101361885347977415827831904465125972681277283243530766501893543832374257674319643447978284232131374047798140761172317是素数
时间差143827ms
对于生成的大素数,我们可以用我们前面写的米勒罗宾算法检测。当然也可以使用Java的BigInteger类判断(使用这个类生成大素数很快,如果有兴趣可以研究一下)
String string="955042930633410289133616296687431777269353980956568253574985061454859846383784618868936295454149058329055354262839296541908590329891268218404276396709186373481902442299599349413886590143757678944807286223232776732690994758060943148907454012806238319657554857310557054678934303822406793932126613431907";
BigInteger a=new BigInteger(string);
if(a.isProbablePrime(1024)) a是素数的概率为1 - 1 / 2^1024
System.out.println("素数");
else
System.out.println("合数");
运行结果:素数
六、源码下载
大整数包的实现(Java)
