Atcoder 刷题（划水）记录

http://agc016.contest.atcoder.jp/tasks/agc016_b
题意：有N只猫，每只猫带着某种颜色的帽子，给出每只猫能看到（即其他N-1只猫）的颜色种数a【i】，问是否可以构造出合法序列。

题解：
本蒟蒻想了挺久的，显然a【i】的顺序没有什么卵用，排个序。
会有一个显然的结论：
  当max-min>1时直接输出No。
max==min 则N==a[1]+1或N>=a[1]*2时 输出Yes，否则输No；
max==min+1 则 设min的个数为cnt，max的个数为N-cnt，
    若cnt>min  或者 (n-cnt)<(a[n]-cnt)*2 输出No；
    否则输出Yes

http://agc016.contest.atcoder.jp/tasks/agc016_c
题意：给出H, W, h ， w 要求构造出长宽为H、W的矩形，每个元素在【-1e9，1e9】间，使得矩阵元素和大于0，每个长宽为h、w的子矩阵元素和小于0，不存在输出No 存在则输出Yes 和合法矩阵。

题解：
想了一下这就是一道思博题啊~~~
显然H%h==0&&W%w==0是输出No
然后只要把正常位置设为一个极大值INF，对于i、j，满足i%h==0&&j%w==0时赋为(1-h*w)*INF-1，显然这样构造对于每个长宽为hw的子矩阵满足和<0,然后和一定大于0。极大值大概取个几千吧，惨痛代价……

http://agc015.contest.atcoder.jp/tasks/agc015_c
题意：给定一个n*m的01矩阵（n，m<=2000）,每次询问一个子矩阵内有多少个1的联通块（能通过上下左右到达即联通），保证两点只有一条路径。Q<=200000

题解：
稍稍想一下会有一个结论，
所求答案为  1的个数-水平相邻的1个数-垂直相邻的1个数
然后这可以O（nm）的代价预处理出一个二维前缀，加加减减即可。注意考虑一下细节（被坑死，调了1h+样例的窝哭晕）

http://agc003.contest.atcoder.jp/tasks/agc003_d
题意：给定N（<=100000）个整数，要求选出最多的数，满足对于任意的i、j， si(<=1e10)∗sj（i！=j） 不为完全立方数.

首先把每个数分解质因数后，指数%3,得到的结果S是唯一的，然后求出其补集，
显然这是若干个相对独立的问题，只要每次取两个集合较大的一个即可。
再判断一下特殊情况，即S为1时只能取一个。

http://agc002.contest.atcoder.jp/tasks/agc002_e
题意：很多堆石子，两人游戏。
每次可以取走数量最多的那堆石子的全部石子，或取走每堆各一个石子。

题解：
我们把一堆石子想象成一个石子个数*1的矩形。 
把矩形从高到低排列变成一个图形。 
我们每次可以删除最低下一行或最左边一列。 
假设有一个点初始在(1,1)，它在(x,y)表示[1,x)的列被删了，[1,y)的行被删了。 
则每次相当于将这个点往上移或往右移，不能操作者输。 
而且可以证明（x，y）和（x-1，y-1）的胜负相同。
所以找到离原点最远的一个点且在```$y=x$```的直线上，判断一该点上面和右边的胜负即可。
（注：边界的胜负情况是01交错的，我zz的认为都是0 ...QAQ）

http://agc001.contest.atcoder.jp/tasks/agc001_d
题意：
给定你a序列，请你重排它并构造一个b序列。
使得两个序列元素和均为n。
对于一个长度为n的字符串，满足如果前a[1]个是回文串，接下来a[2]个是回文串……且前b[1]个是回文串，接下来b[2]个是回文串……那么这个字符串每个字母相同。
题解：

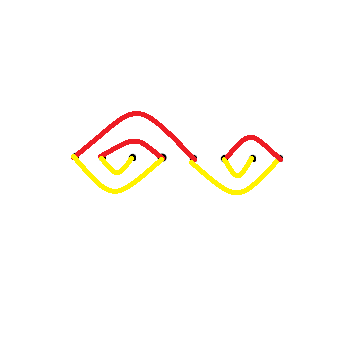
首先看一下上图：
上面是a为5、3 ，b为4、4的情况。
然后相当于整个图像能否一笔画。然后写写画画发现奇数只有放在两边才有解，然后首尾一加一减，
其他b和a一样即可。

/#######################################################/
10.30
A http://agc016.contest.atcoder.jp/tasks/agc016_d
题意:一个序列，一次操作可以将某个位置变成整个序列的异或和。 问最少几步到达目标序列。

写写画画发现操作相当于做一些置换。
所以a、b数组连同异或和Sa，Sb应该是相等的。
排个序后比较一下。不合法则输出-1

将a数组中的值当做点，向b中连边，得到一个一堆环的图。
显然走完一个联通块的代价为其边数
接着会有一个显然结论，若Sa在某个联通块中，则代价可以-1
所以最后答案为 联通块边数+联通块个数-（Sa在某个联通块中）
代码：http://paste.ubuntu.com/25856912/

B http://agc012.contest.atcoder.jp/tasks/agc012_e
题意：一排点，两点间有距离。
初始你有一个驼峰容量v，如果相邻两点距离不超过v你可以自由在这两点行走。
当v大于0时，你可以选择某一时刻突然飞到任意点，这样做后v会减半（下取整）。
问从每个位置初始出发能否到达所有位置。

显然驼峰最多有log种大小。
预处理出l【i】【j】表示从第i个点出发，已经跳过j次，可以到达最右处。
              r【i】【j】同理

然后 f【mask】（maks表示已经跳过的集合，可以理解为把跳跃拆成若干个区间）表示从左往右最远处
        g【mask】同理

 对于每个点i，一开始可以到达的区间为L=l【i】【0】，R=r【i】【0】

 去掉第一次状态后 总跳跃状态T = $(1<<log)-2;$

 当某个状态mask满足 f【mask】>=L+1 且g【T 异或 mask 】<=R-1即可。
 将每个R-1 和g（除掉第一次跳跃未跳的）一起排序
 扫到一个g【mask】，维护一个f【T异或mask】的最大值tmp
 扫到一个询问时，此时前面的g均满足<=R-1,只需满足tmp>=L+1即可。
 代码：http://paste.ubuntu.com/25857026/

C http://agc007.contest.atcoder.jp/tasks/agc007_c
题意：在数轴上有一排点，有坑有球，且距离成等差数列。
每次等概率把某个求往左或往右扔进一个没有球的最近的一个洞里，
问最后每个球的期望路程。

根据期望的性质大概可以得出一个结论，一开始以及每次之后每次滚完，和直接令每一段相等，所得到的答案是一样的。所以直接乱搞即可。
代码:http://paste.ubuntu.com/25857047/

/#######################################################/