Leetcode 第183 场周赛题解

5376. 非递增顺序的最小子序列

将数组 nums 划分为两个子序列 A, B，A 要满足下述两个条件：

• sum(A) > sum(B)
• A 的长度要尽可能的短。

当把 nums 中的所有元素都给 A 时，显然满足第一个条件，因为 nums 中只有正整数。
然后不断的将 A 中最小的元素转移到 B 中，直到无法转移。无法转移的意思是，再转移一个元素就会打破第一条限制。此时 降序排序的 A 即为答案。
实现代码如下：

class Solution {
public:
    vector<int> minSubsequence(vector<int>& nums) {
        sort(nums.begin(), nums.end(), greater<int>());
        int sum = 0; 
        for(auto v : nums) {
            sum += v;
        }
        int ts = 0;
        for(int i = 0; i < nums.size(); i++) {
            ts += nums[i];
            if(ts > sum - ts) {
                return vector<int>(nums.begin(), nums.begin() + i + 1);
            }
        }
        return nums;
    }
};

5377. 将二进制表示减到 1 的步骤数

可以借助链表模拟。首先将 string 转为 list。然后模拟规则处理list。
转成 list 是为了降低最高位进位时的时间复杂度。
设 cnt 为操作计数器。

1. 如果 list.size() == 1 ，处理结束。
2. 如果 list 的最后一个元素为 0，cnt += 1，将最后一个结点弹出。跳转第一步。
3. 如果 list 的最后一个元素为 1，cnt += 1，对最后一个结点加一并模拟进位。需要考虑最高位进位的情况。跳转第一步。

代码如下：

class Solution {
public:
    int numSteps(string s) {
        list<int> node;
        for(int i = 0; i < s.size(); ++i) {
            node.push_back(s[i]-'0');
        }
        int cnt = 0;
        while(node.size() > 1) {
            if(node.back() == 0) {
                cnt++;
                node.pop_back();
            } else {
                cnt++;
                for(auto it = --node.end();;) {
                    if(*it == 1) {
                        *it = 0;
                        if(it == node.begin()) {
                            node.insert(it, 1);
                            break;
                        } else {
                            --it;
                        }
                    } else {
                        *it = 1;
                        break;
                    }
                }
            }
        }
        return cnt;
    }
};

5195. 最长快乐字符串

假设给出数据为 a >= b >= c。其他情况也可经过排序转化为这种情况。

1. 首先拿出 c 个 ‘a’, ‘b’, ‘c’ 进行拼接。
2. 再拿出 b-c 个 ‘a’，‘b’ 进行拼接。此时所有 ‘b’，‘c’ 都已拼接到答案中，仅剩 a-b 个 ‘a’ 未拼接。
3. 然后可以通过暴力枚举将尽可能多的 ‘a’ 插入到答案中。

完成前两步后，答案长这个样子。

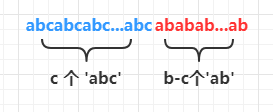
这样插入，可以保证用两个较少的字符隔开最多的字符，从而保证总体长度最长。
代码如下：

class Solution {
    bool check(int pos, const string &str, const string &ch) {
        string a = str;
        a.insert(pos, ch);
        for(int i = 0; i+2 < a.size(); i++) {
            if(a[i] == ch[0] && a[i+1] == ch[0] && a[i+2] == ch[0]) {
                return false;
            }
        }
        return true;
    }
public:
    string longestDiverseString(int a, int b, int c) {
        vector<pair<int, string>> vec;
        vec.push_back(make_pair(a, string("a")));
        vec.push_back(make_pair(b, string("b")));
        vec.push_back(make_pair(c, string("c")));
        sort(vec.begin(), vec.end());
        string str;
        while(vec[0].first > 0) {
            vec[0].first --;
            vec[1].first --;
            vec[2].first --;
            str += vec[2].second;
            str += vec[1].second;
            str += vec[0].second;
        }
        while(vec[1].first > 0) {
            vec[1].first --;
            vec[2].first --;
            str += vec[2].second;
            str += vec[1].second;
        }
        while(vec[2].first > 0) {
            bool flag = false;
            for(int i = 0; i <= str.size(); i++) {
                if(check(i, str, vec[2].second)) {
                    str.insert(i, vec[2].second);
                    flag = true;
                    break;
                }
            }
            if(flag == false) {
                break;
            }
            vec[2].first --;
        }
        return str;
    }
};

5379. 石子游戏 III

容易让人魔怔的零和博弈！Σ(っ °Д °;)っ
为了便于理解，我们假设下标从 1 开始。
设 dp[i] 代表在 [i…n] 上，先手采取最优策略的得分。
因为必须拿 1 或 2 或 3 堆，所以 dp[n] = stoneValue[n]，即只有一堆时，先手必须拿走，无论该数字的正负。
当 i ∈ [1, n-1] 时，先手有多种策略可选，但先手一定会选择让后手得分最少的策略。因为是零和博弈，总数就那些，对手得分少了，自己得分就高。
根据题意，先手共有三种策略 j = 1 或 j = 2 或 j = 3，对应的，在后手的回合，后手会面临三种局面，即从 [i+1, n]，[i+2, n]，[i+3, n] 选取最优解。
当然，后手虽然无法选择面临的局面，但他可以选择每种局面中的最优策略。
而先手虽然无法改变后手的策略选择，但可以决定后手面临的局面，先手必然让后手面临三种局面中得分最少的局面！！

Σ(っ °Д °;)っ 品，细品，品完这两句再看下面！
在局面 [i,n] 中，先手选择一块时，自己的最高得分为：
A = stoneValue[i] + sum(i+1, n) - dp[i+1]
先手选择两块时，自己的最高得分为：
B = stoneValue[i, i+1]+ sum(i+2, n) - dp[i+2]
先手选择两块时，自己的最高得分为：
C = stoneValue[i, i+1,i+2]+ sum(i+3, n) - dp[i+3]
腹黑如先手，肯定会选择得分最大的策略！
再细品一下状态转移方程：当先手选完 j 堆石头后，游戏进入到下一回合！先手变后手，后手变先手! 此时的先手依然会选择最优策略即 dp[i+j]，对于上一局的先手来说，他只能获得剩下的部分，即 sum(i+j, n) - dp[i+j]。
品完上代码

class Solution {
public:
    string stoneGameIII(vector<int>& stoneValue) {
        int dp[50003] = {0};
        int sum = 0;
        for(int n = stoneValue.size(), i = n-1; i >= 0; i--) {
            dp[i] = -0x7FFFFFFE;
            sum += stoneValue[i];
            for(int j = 1; j <= 3; j++) {
                dp[i] = max(dp[i], sum - dp[i+j]);
            }
        }
        if(sum - dp[0] == dp[0]) {
            return "Tie";
        } else if(sum - dp[0] > dp[0]) {
            return "Bob";
        }
        return "Alice";
    }
};