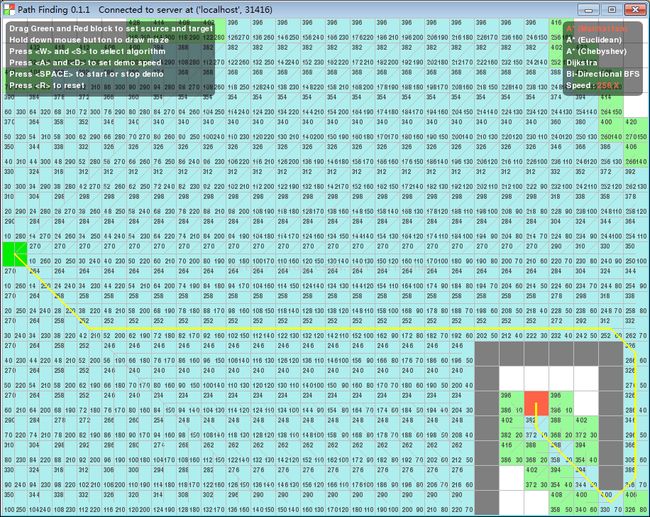
A*寻路算法（曼哈顿距离）

前一些天，在群有人问到A*算法的问题。之前我已经有实现过，并将之放到github上（https://github.com/ATinyAnt/A_Star）；有兴趣的可以下载下来看看。

这里上传了一个相当好的A*算法演示程序，大家可以下载下来看看效果：http://download.csdn.net/detail/a374826954/8781185。

下面描述是摘自清华大学出版社《人工智能》一书：

评价函数的形式如下：

f(n) = g(n) + h(n)

其中，n是被评价的结点。

g*(n)：表示从初始结点s到结点n的最短的耗散值；

h*(n)：表示从结点n到目标结点g的最短的耗散值；

f*(n)=g*(n)+h*(n)：表示从结点s经过结点n到目标结点g的最短路径的耗散值。

而f(n)、g(n)和h(n)则分别表示是对f*(n)、g*(n)和h*(n)3个函数值的估计值，的一种预测。A算法就是利用这种预测，来达到搜索的目的。

当在算法A的评价函数中，使用的启发函数h(n)是处于h*(n)的下界范围，即满足h(n)≤h*(n)时，则把这个算法称为算法A*。

需要说明的是，程序由于增加了一些调试信息，稍微会比实际慢一些。

下面看一下程序演示界面：

白格子表示通路，黑格子表示阻挡。

这里的黑格子是随机生成，在以下代码产生：

 

(function(){
	map.init(0.3);
	map.createUI();
})();

随机数为0.3，当设置为0时，则全部都是通路。

 

说说3个按钮：

“设置阻挡”：按下这个按钮后可以通过鼠标左键自定义阻挡区域，方便测试。

“closed”：显示已经被扩展并放到closed表的节点信息。显示信息以C：开头；显示4个数据分别是f，g，h和扩展索引；需要注意的是扩展索引不一定是连续的，因为同一个节点可能被多次扩展。

“open”：显示剩余剩余的open表节点信息。显示信息以O：开头；显示3个数据分别是f，g和h。

 

其实一些人搞不懂A*算法，主要是搞不懂f，g，h是怎样取值的。

下面举个例子：

从广州到北京（最好打开百度地图对比着看，以下距离不等于实际城市间的距离）

换言之，广州就是起始点，北京就是目标点。

广州到广州的距离是0，也就是g=0；广州到北京的直线距离是5000，也就是h=5000。f=g+h，f=5000。

将广州放进open表，扩展广州这个节点，并将广州从open表删除，放进closed表；得到重庆和上海。

 

广州到重庆的距离是2500，也就是重庆这个节点的g=2500；重庆到北京的直线距离是4500，也就是h=4500；f=7000。

将重庆放进open表。

 

广州到上海的距离是3000，也就是上海这个节点的g=3000；上海到北京的直线距离是3000，也就是h=3000；f=6000。

将上海放进open表；由于上海的f小于重庆的f，在open表中上海节点在重庆节点前面。

 

扩展上海这个节点，发现找到了北京，于是搜索结束。最后的路径就是广州-上海-北京。

本程序的核心代码是：

 

search : function(){
    	while(1){
    		if (map.openTable.length == 0){
	    		break;
	    	}
            var _fMinNode = map.openTable.shift();
            if (_fMinNode.place == 2){
            	continue;
            }
            
            map.searchAround(_fMinNode);
            _fMinNode.index = globalIndex;
            globalIndex++;
            _fMinNode.place = 2;
			closedTable.push(_fMinNode);
            if (map.endNode == _fMinNode){
            	break;
            }
        }
    },
    
    searchAround : function(node){
        var nodeX;
        var nodeY;

        for (var x = -1; x <= 1; x++) 
        {
            nodeX = node.x + x;
            for (var y = -1, mapNode, _obj, tmpNode; y <= 1; y++) 
            {
                nodeY = node.y + y;
                //剔除本身
                if (x === 0 && y === 0) continue;
                if (nodeX >= 0 && nodeY >= 0 && nodeX < map.gridWidth && nodeY < map.gridHeight) 
                {
                    mapNode = map.data[nodeX][nodeY];
                    if (mapNode.isRoadBlock){
                    	continue;
                    }
					_obj = map.getFGH(node, mapNode);
					do
					{
						if (mapNode.place == 2){
							if (_obj.G >= mapNode.obj.G){
								break;
							}
						}
						else if (mapNode.place == 1){
							// 单调限制
							if (mapNode.obj.G <= _obj.G){
								continue;
							}
						}
                        
                        mapNode.obj = _obj;
                        mapNode.front = node;
                        mapNode.place = 1;
                        map.insertOpenTable(mapNode);
					}while(0)
                };
            };
        };
    },

工作流程就是循环顺序遍历open表(根据f值进行排序)，扩展读取出来的节点，直到找到目标点。

 

其中getFGH就是计算该节点的f，g，h信息。

你可以看到代码里面有写着// 单调限制的注释；再举同一个例子说明一下。

广州还扩展出一个节点：武汉。

武汉的f=5900，g=2400，h=3500。这时候是先扩展武汉，于是又找到了上海。

武汉到上海的距离是1900。这时候经过武汉到上海的节点信息是g=2400+1900=4300，h是不变的也是3000。

上海节点mapNode之前保存的g=3000，现在算出经过武汉到上海的距离是g=4300。因此经过武汉到上海比直接到上海的距离远，因此不将f，g，h替换放到open表。

这就是单调限制。

下面是本篇文章代码及演示程序的效果图：

A*算法的不足：

当目标点是位于死路区域，则A*算法会遍历整个地图。这明显是低效率的。