图的BFS和DFS原理及实例分析（java）

BFS和DFS是图的两种遍历方式，是最简单的图搜索算法。

本文将给出给出BFS和DFS的以下几种实现方式：
1、使用队列Queue实现图的BFS遍历
2、递归实现图的DFS遍历
3、使用栈Stack迭代实现图的DFS遍历

---

一、BFS（广度优先搜索算法）

BFS算法之所以叫做广度优先搜索，是因为它始终将已发现的顶点和未发现的之间的边界，沿其广度方向向外扩展。亦即，算法首先会发现和s距离为k的所有顶点，然后才会发现和s距离为k+1的其他顶点。

同深度优先搜索相反，BFS宽度优先搜索每次选择深度最浅的节点优先扩展。并且当问题有解时，宽度优先算法一定能够找到解，并且在单位耗散时间的情况下，可以保证找到最优解。

---

二、DFS（深度优先搜索算法）

DFS算法利用递归方式实现，和BFS不同的是BFS搜索产生的始终是一棵树，而DFS产生的可能会使一个森林。

对于深度优先搜索算法的思想。在一般情况下，当问题有解时，深度优先搜索不但不能够保证找到最优解，也不能保证找到解。如果问题状态空间有限，则可以保证找到解；但是当问题的状态空间无限时，则可能陷入“深渊”而找不到解。为此我们可以利用回溯算法中的思想，可以加上对搜索的深度限制。从而实现对于搜索深度的限制。当然深度限制设置必须合理，深度过深则影响搜索的效率，深度过浅时，则可能影响找到问题的解。

使用栈实现DFS思路关键点：

1、首先明确整个DFS主要便是对于栈进行操作，就是在顶点压栈和弹栈过程中我们需要进行的操作；

2、利用DFS的思想，深度遍历节点。直到栈内元素为空位置；

3、何时进行压栈：对于栈顶顶点，看其邻接顶点中是够存在未被遍历过得白色顶点，若有则对将其压栈，然后再对栈顶元素进行操作；

4、如果栈顶顶点的所有邻接顶点都是被遍历过的灰色顶点，则将栈顶元素弹栈，然后再对现在的栈顶元素进行操作；

5、算法结束时，所有元素均被遍历过即为灰色，并且栈已经为空。

---

三、BFS和DFS实现（java）

1、Vertex对象类

public class Vertex1 {
    String verName;
    String color;  
    int discoverTime;
    int finishTime;
    Vertex1 nextNode;
}

2、Graph对象类

public class Graph1 {
    Vertex1[] vertexArray=new Vertex1[100];
    int verNum=0;
    int edgeNum=0;
}

3、核心实现类

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
import java.util.Stack;

/**
 * 
无权有向图和无向图的构建以及实现了图的BFS遍历和DFS遍历:
 * 1>.使用队列Queue实现图的BFS遍历;
 * 2>.递归实现图的DFS遍历;
 * 3>.使用栈Stack迭代实现图的DFS遍历。
 * @author King
 */
public class CreateGraph1 {
    int time=0;
    Stack stackVertex=new Stack();

    public static void main(String[] args) {
        Graph1 graph=new Graph1();
        CreateGraph1 createGraph=new CreateGraph1();
        createGraph.initialGraph(graph);
        createGraph.outputGraph(graph);
//      System.out.println("DFS搜索路径为(递归实现)：");
//      createGraph.DFS(graph);
        System.out.println("DFS搜索路径为(栈实现):");
        createGraph.stackMain(graph);
//      System.out.println("BFS搜索路径为：");
//      createGraph.BFS(graph);
    }

    /**
     * 根据用户输入的string类型的顶点返回该顶点
     * @param graph 图
     * @param str 输入数据
     * @return返回一个顶点
     */
    public Vertex1 getVertex(Graph1 graph,String str){
        for(int i=0;iif(graph.vertexArray[i].verName.equals(str)){
                return graph.vertexArray[i];
            }
        }
        return null;
    }

    /**
     * 根据用户输入的数据初始化一个图，以邻接表的形式构建!
     * @param graph 生成的图
     */
    public void initialGraph(Graph1 graph){
        @SuppressWarnings("resource")
        Scanner scan=new Scanner(System.in);
        System.out.println("请输入顶点数和边数：");
        graph.verNum=scan.nextInt();
        graph.edgeNum=scan.nextInt();

        System.out.println("请依次输入定点名称：");
        for(int i=0;inew Vertex1();
            String name=scan.next();
            vertex.verName=name;
            vertex.color="white";
            vertex.discoverTime=0;
            vertex.finishTime=0;
            vertex.nextNode=null;
            graph.vertexArray[i]=vertex;
        }

        System.out.println("请依次输入图的便边：");
        for(int i=0;iif(v1==null)
                System.out.println("输入边存在图中没有的顶点！");
            Vertex1 v2=new Vertex1();
            v2.verName=folV;
            v2.nextNode=v1.nextNode;
            v1.nextNode=v2;

//          紧接着下面注释的代码加上便是构建无向图的，不加则是构建有向图的！
//          Vertex1 reV2=getVertex(graph,folV);
//          if(reV2==null)
//              System.out.println("输入边存在图中没有的顶点！");
//          Vertex1 reV1=new Vertex1();
//          reV1.verName=preV;
//          reV1.nextNode=reV2.nextNode;
//          reV2.nextNode=reV1;
        }
    }

    /**
     * 输入图的邻接表
     * @param graph 待输出的图
     */
    public void outputGraph(Graph1 graph){
        System.out.println("输出图的邻接链表为：");
        for(int i=0;iwhile(current!=null){
                System.out.print("-->"+current.verName);
                current=current.nextNode;
            }
            System.out.println();
        }
    }

    /**
     * DFS遍历辅助函数，标记颜色是辅助，即根据顶点返回其下标
     * @param vertex 顶点
     * @param graph 图
     * @return返回下标
     */
    public int index(Vertex1 vertex,Graph1 graph){
        for(int i=0;iif(vertex.verName.equals(graph.vertexArray[i].verName))
                return i;
        }
        return -1;
    }

    /**
     * DFS深度优先遍历初始化
     * @param graph 图
     */
    public void DFS(Graph1 graph){
        for(int i=0;iif(graph.vertexArray[i].color.equals("white")){
                DfsVisit(graph.vertexArray[i],graph);
                System.out.println();
            }
        }
    }

    /**
     * DFS递归函数
     * @param vertex 顶点
     * @param graph 图
     */
    public void DfsVisit(Vertex1 vertex,Graph1 graph){
        vertex.color="gray";
        time=time+1;
        vertex.discoverTime=time;
        System.out.print(vertex.verName+"-->");

        Vertex1 current=vertex.nextNode;
        while(current!=null){
            Vertex1 currentNow=getVertex(graph, current.verName);
            if(currentNow.color.equals("white"))
                DfsVisit(currentNow,graph);
            current=current.nextNode;
        }
        vertex.color="black";
        time=time+1;
        vertex.finishTime=time;
    }

    /**
     * 寻找一个节点的邻接点中是否还有白色节点
     * @param vertex 顶点
     * @param graph 图
     * @return 返回白色节点或是null
     */
    public Vertex1 getAdj(Graph1 graph,Vertex1 vertex){
        Vertex1 ver=getVertex(graph, vertex.verName);
        Vertex1 current=ver.nextNode;
        if(current==null)
            return null;
        else{
            Vertex1 cur=getVertex(graph, current.verName);
            while(current!=null && cur.color.equals("gray")){
                current=current.nextNode;
            }
            if(cur.color.equals("white")){
                Vertex1 currentNow=getVertex(graph, current.verName);
                return currentNow;
            }else{
                return null;
            }
        }

    }

    /**
     * 通过栈实现dfs遍历
     * @param graph 图
     * @param vertex 顶点
     */
    public void stackOperator(Graph1 graph,Vertex1 vertex){
        vertex.color="gray";
        stackVertex.push(vertex);
        System.out.print(vertex.verName+"-->");

        while(!stackVertex.isEmpty()){
            Vertex1 ver=stackVertex.peek();
            Vertex1 current=getAdj(graph,ver);
            if(current!=null){
                stackVertex.push(current);
                current.color="gray";
                System.out.print(current.verName+"-->");
            }else{
                stackVertex.pop();
            }
        }
    }

    /**
     * DFS遍历主函数
     * @param graph
     */
    public void stackMain(Graph1 graph){
        for(int i=0;iif(graph.vertexArray[i].color.equals("white")){
                stackOperator(graph,graph.vertexArray[i]);
                System.out.println();
            }
        }
    }

    /**
     * BFS广度优先搜索实现
     * @param graph 图
     */
    public void BFS(Graph1 graph){
        Vertex1 current=graph.vertexArray[0];
        current.color="gray";
        time=time+1;
        current.discoverTime=time;

        Queue queue=new LinkedList();
        queue.offer(current);
        while(queue.peek()!=null){
            Vertex1 ver=queue.poll();
            time=time+1;
            ver.finishTime=time;
            System.out.print(ver.verName+"-->");

            Vertex1 cur=ver.nextNode;
            while(cur!=null){
                Vertex1 curNow=getVertex(graph, cur.verName);
                if(curNow.color.equals("white")){
                    curNow.color="gray";
                    time=time+1;
                    curNow.discoverTime=time;
                    queue.offer(curNow);
                }
                cur=cur.nextNode;
            }
        }
        System.out.println("null");
    }
}

/*
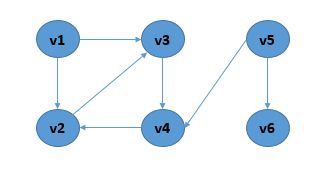
DFS测试图的边：
v1 v2
v1 v3
v2 v3
v3 v4
v4 v2
v5 v4
v5 v6

BFS测试图的边(10)：
v1 v2
v1 v4
v2 v3
v4 v5
v4 v8
v5 v6
v5 v7
v5 v8
v6 v7
v7 v8
*/

BFS测试所用的无向图为：

BFS测试输入数据：

测试结果为：

---

DFS测试所用的有向图为：

DFS测试输入数据
：

DFS测试结果：

关于BFS和DFS的特征以及它们关于非启发式图搜索算法的知识后续将进行补充。如有何问题欢迎指正，谢谢！