全局路径规划：图搜索算法介绍6(A star)Matlab算法实现

本文接：全局路径规划：图搜索算法介绍2(A star)
https://blog.csdn.net/gophae/article/details/103061702

% This is YunchengJIANG from HKUST
% Used for Motion Planning for Mobile Robots @ELEC 5660
% HKUST  香港科大
close all; clear all; clc;

set(gcf, 'Renderer', 'painters');
set(gcf, 'Position', [500, 50, 700, 700]);

% Environment map in 2D space 
xStart = 1.0;
yStart = 1.0;
% xTarget = 9.0;
% yTarget = 9.0;
% MAX_X = 10;
% MAX_Y = 10;
xTarget = 19.0;
yTarget = 19.0;
MAX_X = 20;
MAX_Y = 20;
map = obstacle_map(xStart, yStart, xTarget, yTarget, MAX_X, MAX_Y);

path = A_star_search(map, MAX_X,MAX_Y,xTarget, yTarget);

visualize_map(map, path,MAX_X);

function path = A_star_search(map,MAX_X,MAX_Y,xTarget, yTarget)
%%
%This part is about map/obstacle/and other settings
    %pre-process the grid map, add offset

%%
% Waypoint Generator Using the A* 
    size_map = size(map,1);
    Y_offset = 0;
    X_offset = 0;
    
    %Define the 2D grid map array.
    %Obstacle=-1, Target = 0, Start=1, free space =2
    MAP=2*(ones(MAX_X,MAX_Y));
    
    %Initialize MAP with location of the target
    xval=floor(map(size_map, 1)) + X_offset;
    yval=floor(map(size_map, 2)) + Y_offset;
    xTarget=xval;
    yTarget=yval;
    MAP(xval,yval)=0;
    
    %Initialize MAP with location of the obstacle
    for i = 2: size_map-1
        xval=floor(map(i, 1)) + X_offset;
        yval=floor(map(i, 2)) + Y_offset;
        MAP(xval,yval)=-1;
    end 
    
    %Initialize MAP with location of the start point
    xval=floor(map(1, 1)) + X_offset;
    yval=floor(map(1, 2)) + Y_offset;
    xStart=xval;
    yStart=yval;
    MAP(xval,yval)=1;

    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    %LISTS USED FOR ALGORITHM
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    %OPEN LIST STRUCTURE
    %--------------------------------------------------------------------------
    %IS ON LIST 1/0 |X val |Y val |Parent X val |Parent Y val |h(n) |g(n)|f(n)|
    %--------------------------------------------------------------------------
    OPEN=[];
    %CLOSED LIST STRUCTURE
    %--------------
    %X val | Y val |
    %--------------
    % CLOSED=zeros(MAX_VAL,2);
    CLOSED=[];

    %Put all obstacles on the Closed list
    k=1;%Dummy counter
    for i=1:MAX_X
        for j=1:MAX_Y
            if(MAP(i,j) == -1)
                 CLOSED(k,1)=i;
                CLOSED(k,2)=j;
                k=k+1;
            end
       end
    end
    CLOSED_COUNT=size(CLOSED,1);
    %set the starting node as the first node
    xNode=xval;
    yNode=yval;
    OPEN_COUNT=1;
    goal_distance=distance(xNode,yNode,xTarget,yTarget);
    path_cost=0;
    OPEN(OPEN_COUNT,:)=insert_open(xNode,yNode,goal_distance,path_cost,goal_distance);
    OPEN(OPEN_COUNT,(6:7)) = [0,0];
    %     OPEN(OPEN_COUNT,1)=0;
%     NoPath=1;
%%
%This part is your homework
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% START ALGORITHM
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

i = 1;

flag =0;

while(flag ~=1) %you have to dicide the Conditions for while loop exit 
        [i_min,flag] = min_fn(OPEN,OPEN_COUNT,xTarget,yTarget);
     %
     %finish the while loop
     %
 
   %End of While Loop
    
    %Once algorithm has run The optimal path is generated by starting of at the
    %last node(if it is the target node) and then identifying its parent node
    %until it reaches the start node.This is the optimal path
    node_x = OPEN(i_min,1);
    node_y = OPEN(i_min,2);
     
    gn = OPEN(i_min, 4);
    
    [exp_array,Flag] =expand_array(node_x,node_y,gn,...
    xTarget,yTarget,CLOSED,OPEN,MAX_X,MAX_Y);

%     OPEN((end+1):(end + size(exp_array,1)),:)= exp_array;
    
    for ce=1:size(exp_array,1)
         %if ce in open, continue. or add it to open
         in_open=0;
        for c1=1:OPEN_COUNT
            
            if(exp_array(ce,1) == OPEN(c1,1) && exp_array(ce,2) == OPEN(c1,2))
                in_open=1;
                if exp_array(ce,5) < OPEN(c1,5)
                    OPEN(c1,:) = exp_array(ce,:);
                end
           break
            end
            
        end%End of for loop to check if a successor is on closed list.
         if (in_open==0)
             OPEN_COUNT=OPEN_COUNT+1;
              OPEN(OPEN_COUNT,:)=exp_array(ce,:);
         end
    end


    traj_path_search(i,:) = [OPEN(i_min,1:2) OPEN(i_min,6:7)];
    
    OPEN(i_min,:) = [ ];
    CLOSED_COUNT=CLOSED_COUNT+1;
    CLOSED(CLOSED_COUNT,1)=node_x;
    CLOSED(CLOSED_COUNT,2)=node_y;
    
    OPEN_COUNT = size(OPEN,1);
    
%     [i_min,flag] = min_fn(OPEN,OPEN_COUNT,xTarget,yTarget) ;
    
     i= i+1;

    %
    %How to get the optimal path after A_star search?
    %please finish it
    %
    
end

traj = traj_path_search ;
path(1,:) = traj (end,1:2);
k =1;
 pin = traj(end,:);
 condi = 0;
 while condi ==0
for i = 1:length(traj)
   
    if traj(i,1) == pin(3) && traj(i,2) ==pin(4)
        path(k+1,:) = [pin(3), pin(4)];
         k = k+1;
         pin = traj(i,:);
    end
end
  if pin(1)== traj(1,1) &&pin(2) ==traj(1,2)
        condi =1; 
  end
 end
 path = [[xTarget, yTarget];path(1:end,:)]
end

function dist = distance(x1,y1,x2,y2)
%This function calculates the distance between any two cartesian 
%coordinates.
%   Copyright 2009-2010 The MathWorks, Inc.
dist= sqrt((x1-x2)^2 + (y1-y2)^2);
% dist = abs(x1-x2)  + abs(y1-y2)
end

function [exp_array,Flag]=expand_array(node_x,node_y,gn,xTarget,yTarget,CLOSED,OPEN,MAX_X,MAX_Y)
    %Function to return an expanded array
    %This function takes a node and returns the expanded list
    %of successors,with the calculated fn values.
    %The criteria being none of the successors are on the CLOSED list.
    %
    %Copyright 2009-2010 The MathWorks, Inc.
    
    %EXPANDED ARRAY FORMAT
    %--------------------------------
    %|X val |Y val ||h(n) |g(n)|f(n)|
    %--------------------------------
    
    exp_array=[];
    exp_count=1;
    c2=size(CLOSED,1);
    c3 = size(OPEN,1);%Number of elements in CLOSED including the zeros
    for k= 1:-1:-1
        for j= 1:-1:-1
            if (k~=j || k~=0)  %The node itself is not its successor
                s_x = node_x+k;
                s_y = node_y+j;
                if( (s_x >0 && s_x <=MAX_X) && (s_y >0 && s_y <=MAX_Y))%node within array bound
                    Flag=1;                    
                    for c1=1:c2
                        if(s_x == CLOSED(c1,1) && s_y == CLOSED(c1,2))
                            Flag=0;
                        end
                    end
                    %End of for loop to check if a successor is on closed list.
                    if Flag == 1
                        exp_array(exp_count,1) = s_x;
                        exp_array(exp_count,2) = s_y;
                        exp_array(exp_count,3) = distance(xTarget,yTarget,s_x,s_y);%distance between node and goal,hn
                        exp_array(exp_count,4) = gn+distance(node_x,node_y,s_x,s_y);%cost of travelling to node，gn
                        exp_array(exp_count,5) =1* exp_array(exp_count,3)+exp_array(exp_count,4);%fn
                        exp_array(exp_count,6) = s_x -k;
                        exp_array(exp_count,7) = s_y - j;  
                        exp_count=exp_count+1;  
                    end%Populate the exp_array list!!!
                end% End of node within array bound
            end%End of if node is not its own successor loop
        end%End of j for loop
    end%End of k for loop    
end

function new_row = insert_open(xval,yval,hn,gn,fn)
%Function to Populate the OPEN LIST
%OPEN LIST FORMAT
%--------------------------------------------------------------------------
%IS ON LIST 1/0 |X val |Y val |Parent X val |Parent Y val |h(n) |g(n)|f(n)|
%-------------------------------------------------------------------------
%   Copyright 2009-2010 The MathWorks, Inc.
% new_row=[1,6];
% new_row(1,1)=0;
new_row(1,1)=xval;
new_row(1,2)=yval;
% new_row(1,4)=parent_xval;
% new_row(1,5)=parent_yval;
new_row(1,3)=hn;
new_row(1,4)=gn;
new_row(1,5)=fn;
end

function [i_min,flag] = min_fn(OPEN,OPEN_COUNT,xTarget,yTarget)
%Function to return the Node with minimum fn
% This function takes the list OPEN as its input and returns the index of the
% node that has the least cost
%
%   Copyright 2009-2010 The MathWorks, Inc.

 temp_array=[];
 k=1;
 flag=0;
 goal_index=0;
 for j=1:OPEN_COUNT
         temp_array(k,:)=[OPEN(j,:) j]; 
         if (OPEN(j,1)==xTarget && OPEN(j,2)==yTarget)
             flag=1;
              goal_index=j;%Store the index of the goal node
         end
         k = k+1;
 end %Get all nodes that are on the list open

 if flag == 1 % one of the successors is the goal node so send this node
     i_min=goal_index;
 end
 
 if (size(temp_array) ~= 0)%(size(temp_array,1) ~= 0) &&
  [min_fn,temp_min]=min(temp_array(:,5));%Index of the smallest node in temp array
  i_min = temp_min;
%   i_min=temp_array(temp_min,6);%Index of the smallest node in the OPEN array
 else
     i_min=-1;%The temp_array is empty i.e No more paths are available.
 end
end

 function map = obstacle_map(xStart,yStart,xTarget,yTarget,MAX_X,MAX_Y)
%This function returns a map contains random distribution obstacles.
    rand_map = rand(MAX_X,MAX_Y);
    map = [];
    map(1,1) = xStart;
    map(1,2) = yStart;
    k=2;
    obstacle_ratio = 0.275;
    for i = 1:1:MAX_X
        for j = 1:1:MAX_Y
            if( (rand_map(i,j) < obstacle_ratio) && (i~= xStart || j~=yStart) && (i~= xTarget || j~=yTarget))
                map(k,1) = i;
                map(k,2) = j;
                k=k+1;
            end    
        end
    end
    map(k,1) = xTarget;
    map(k,2) = yTarget;
 end

function visualize_map(map,path,MAX_X)
%This function visualizes the 2D grid map 
%consist of obstacles/start point/target point/optimal path.

    % obstacles
    for obs_cnt = 2: size(map, 1) - 1
        scatter(map(obs_cnt, 1)-0.5,map(obs_cnt, 2)-0.5,250,155,'filled');
        hold on;
        grid on;
        %grid minor;
        axis equal;        
        axis ([0 MAX_X 0 MAX_X ]);
        hold on;
    end
    % start point
    scatter(map(1, 1)-0.5, map(1, 2)-0.5,'b','*');
    hold on;
    % target point
	scatter(map(size(map, 1), 1)-0.5, map(size(map, 1), 2)-0.5, 'r','*');
    hold on;
    %optimal path

    for path_cnt = 2:size(path,1)
        scatter(path(path_cnt,1)-0.5,path(path_cnt,2)-0.5,'*b');
        hold on;
    end
end

整个函数是直接写在一个main 里面，下载后可以直接运行，效果如图。


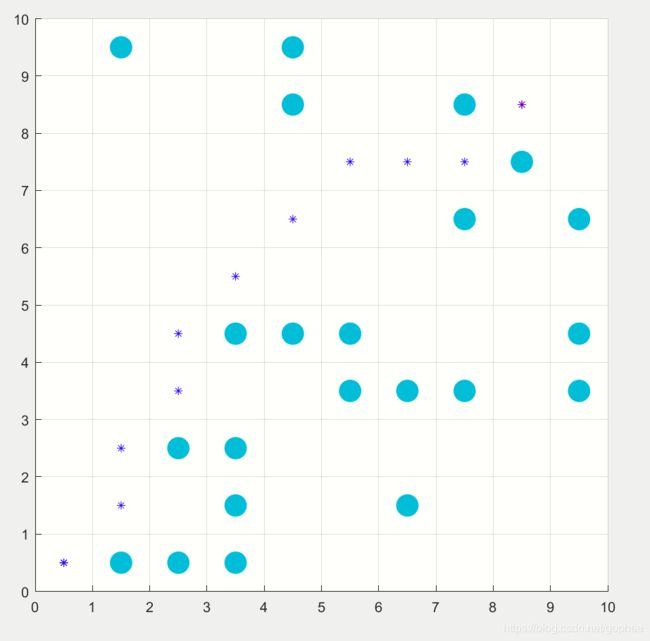
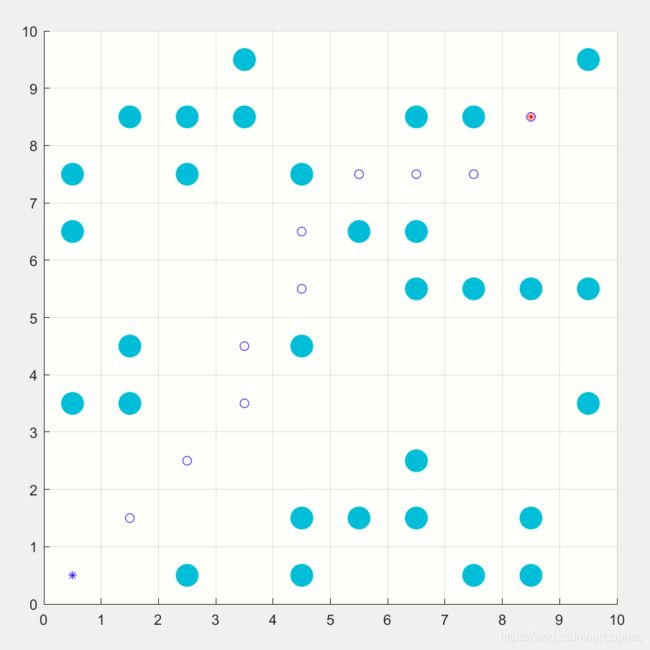
最后值的强调的一个点就是伪代码中的：

if g(m) > g(n)+ Cnm
	g(m) = g(n) + Cnm

再次回顾一下，意思就是在拓展节点的时候，看看新拓展到的节点是不是已经存在open list里面，如果已经在open list里面，就比较一下open list里面存放的这个节点的cost g(m)是不是比新拓展过来的节点的cost g(n) + Cnm(这个是从n节点拓展过来的节点)要大，如果大，那么说明从n新拓展过来的节点是更合理的到达这个节点m的节点，我们要把openlist里面关于这个节点的信息更新为现在的最新信息。

对应代码中的部分就是：

     if(exp_array(ce,1) == OPEN(c1,1) && exp_array(ce,2) == OPEN(c1,2))
                in_open=1;
                if exp_array(ce,5) < OPEN(c1,5)
                    OPEN(c1,:) = exp_array(ce,:);
                end
           break
            end

先看看在不在open list, 如果符合要求就替换掉他。切记，这步很多人经常忘记，出来的轨迹极有可能是次优的。比如下图：