BFS——广度优先搜索的简单易懂入门心得
BFS(广度优先搜索)。
本文应用的语言为C++。
在了解之前,稍微简单介绍一下C++库里STL里的 queue(队列),一个数据“先进先出”的数据结构。
首先调用库queue
定义:queue<数据类型>队列名称;
.push( 数据 );将数据加入队列
.pop();将队首数据弹出队列
.front();取出队列首的数据,但不删除。
为什么需要用到队列呢?
假设我们建立了一棵树,想要搜索其中的某个节点。
如果我们学习了DFS我们知道,DFS是从根节点开始,选择一条树枝,完全搜寻一棵树枝上的所有节点后找不到后,才会递归回去搜寻另一条树枝上面的节点。
有一个特点,就是我们正在处理的那个节点一定来自同枝干上的父节点。
即,现在处理的节点是刚才处理的节点的分支。刚处理完的节点的连线是“竖直”的。
而BFS不同,它是搜寻到一个树枝的节点后,再处理其他树枝同样高度的节点后,才走原树枝到下一个高度的节点。刚处理完的节点连线是“水平”的。
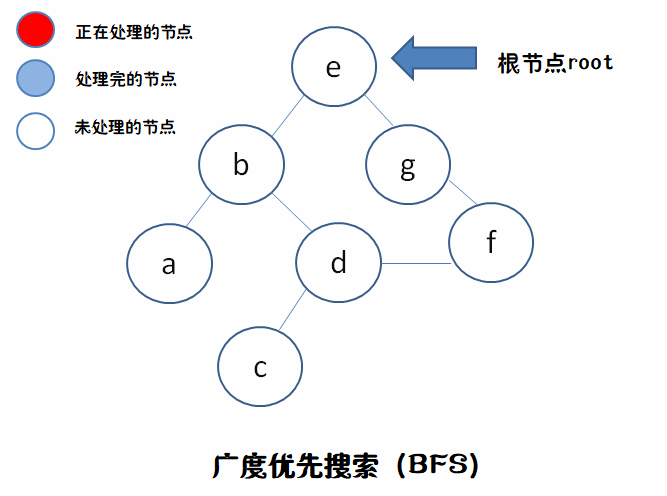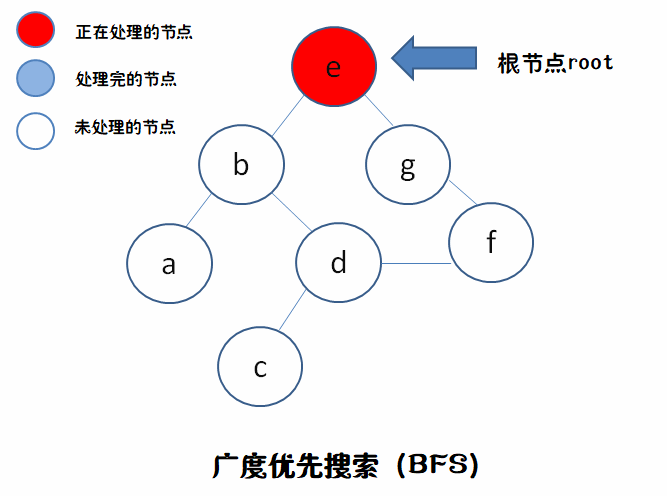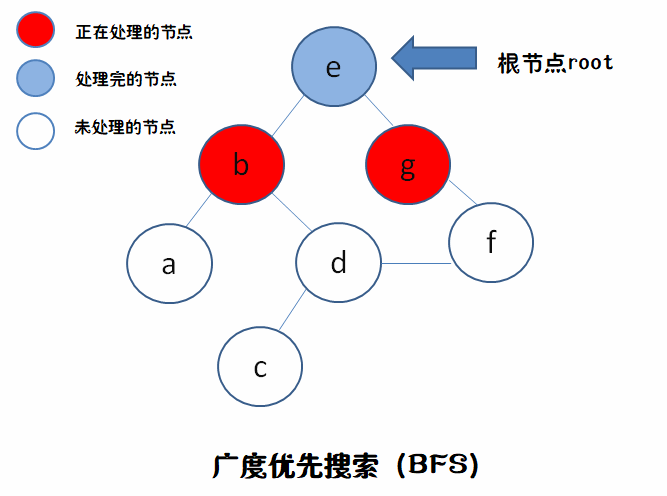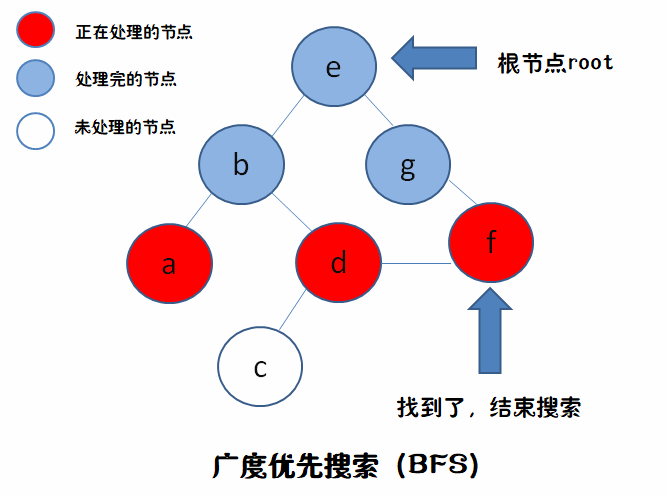
我们来个例子,建立一棵树:
树根就是 e ,假设我们要找 f 吧。方向是从上到下,从左到右
我们来用动态图来描述DFS和BFS不同的行为。
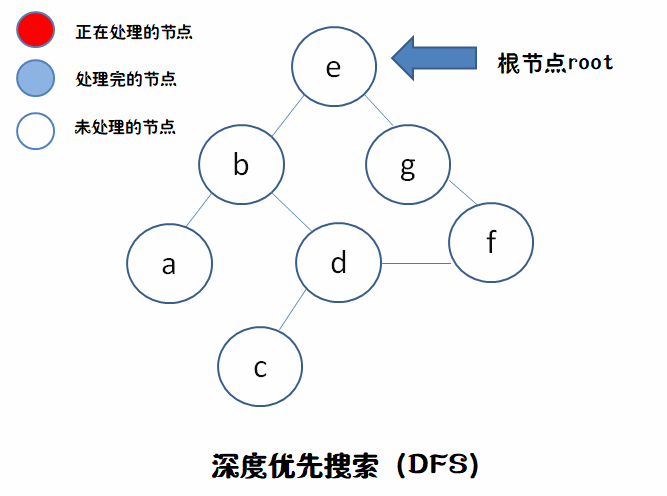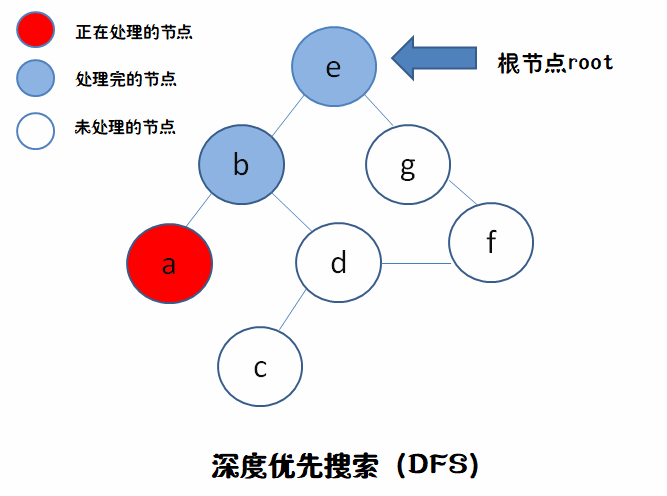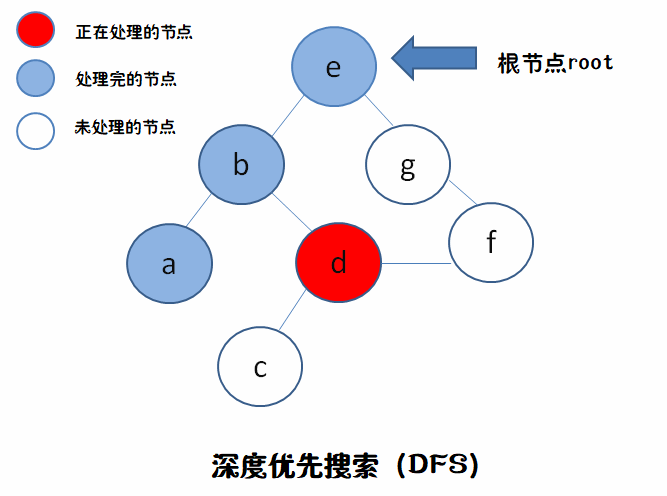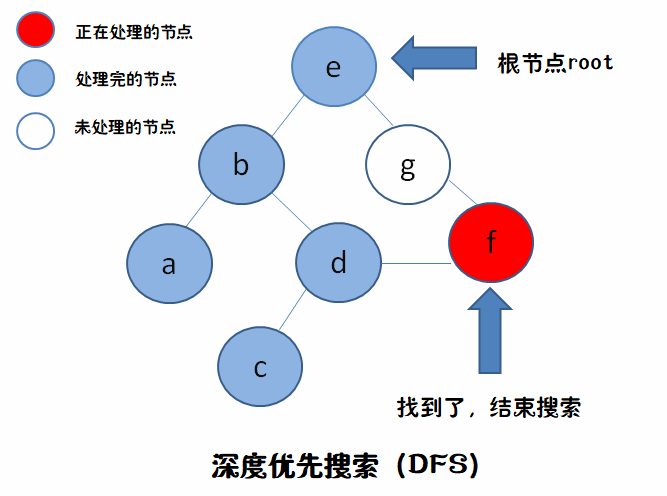
e->b->a
e->b->d->c
是不是像一条“竖直线”?,不到最底不回头。
b->g
a->d->f
是不是像一条“水平”线?,走完一层再走下一层。
然后回到最初的问题,为什么要用queue?
因为每次从队列里拿出来的要处理节点,并不是刚才就处理完的节点的分支,而是在此之前就已经处理完的节点的分支(“先进先出”)。就如图中,我们处理完g,把它的分支f放到队伍最后面,下一个要处理的是在g之前就已经处理完的,b的分枝a,然后到d,最后才到f。
如果我们用栈(stack先进后出)的话,要处理的节点是刚才节点的分支。就如图中,我们处理完b,按照由左往右顺序,先处理掉它的左分支a,而不是处理g。
然后因为b和f都有相同的分支d,所以在放节点进入队列的时候要先创立一个数组存放记录已进过队列里的节点,已进过队列里的节点不能重复进入,以防一个节点重复“开花”造成系统崩溃。
/注意:其实这里的树并不是严格的“树”,应该是数据类型里的图表,文中称树是为了方便描述。现实中有树长成圈那样的吗/dog,有当我没说XD/
全代码:
#includesaveChar<
}
if(p->L!=NULL){
ShowAndRecord(p->L);
}
if(p->R!=NULL){
ShowAndRecord(p->R);
}
}
//struct tree//节点的模板
//{
//char saveChar;//存字母
//struct tree*L;//存节点左边的节点
//struct tree*R;//存节点右边的节点
//};
struct tree*used[50];//记录放进过队列里的节点
int UsedCount;//记录放进去过的节点数
bool Used(struct tree*p)//判断节点有没有放进队列,即有没有被探访过,有则返回true,否则false
{
for(int i=0;i<UsedCount;i++){
if(p==used[i]){return true;break;}
}
return false;
}
void bfs(struct tree*root,char Find)//函数本体,传入根节点和要做的字母
{
queue<struct tree*>que;//建立一个队列
que.push(root);//将第一个节点放进队列,准备让它“发芽”
used[UsedCount++]=root;//记录用过的节点,这里将第一个节点放进去
struct tree*saveNode;//用来储存从队列中拿出来的节点
int steps=0;//记录处理节点的个数
int ok=0;//判断是否能找到
while(!que.empty())//一直处理,直到队列中已经没有节点,即树中每一个节点已经被处理完
{
saveNode=que.front();//取出队列中第一个节点
que.pop();//取出了队列里当然就没了
if(Find==saveNode->saveChar)//如果要找的字母正好是节点里存储的字母
{
cout<<"找到了"<<endl;
cout<<"一个处理了"<<steps+1<<"个节点"<<endl;
ok=1;//找到了就标记
break;//找到了就离开循环,结束寻找
}
else{
cout<<Find<<" 和 "<<saveNode->saveChar<<endl;//如果不是,看一下是在和谁比较,准备走到树的下一层
if(saveNode->L!=NULL&&!Used(saveNode->L))//如果节点左边还有节点,而且还没放进过队列
{
que.push(saveNode->L);//那就放进去呗
used[UsedCount++]=saveNode->L;//记录
}
if(saveNode->R!=NULL&&!Used(saveNode->R))//右边如果由节点,同理
{
que.push(saveNode->R);
used[UsedCount++]=saveNode->R;
}
}
steps++;//一个循环一个节点,处理完毕
}
if(!ok){cout<<"找不到"<<endl;}
return;
}
int main()
{
//输入
//6
//e
//b
//g
//a
//d
//c
//和一个要找的字母
int n;
cin>>n;
char input;
struct tree *p;
struct list L;
L.head=NULL;
for(int i=0;i<n;i++){
p=(struct tree*)malloc((sizeof(struct tree)));
cin>>input;
p->saveChar=input;
p->L=NULL;
p->R=NULL;
if(L.head==NULL){
L.head=p;
}else{
struct tree *prep=L.head;
putin(p,prep);
}
}
ShowAndRecord(L.head);
p=(struct tree*)malloc((sizeof(struct tree)));
p->saveChar='f';
p->L=NULL;
p->R=NULL;
c->R=p;
f->L=p;
char Find;
cout<<"请输入要寻找的字母:";
cin>>Find;
bfs(L.head,Find);
return 0;
}
结果:


于是看动态图我们可以看到,BFS可以更地找到解(免除了递归)。且最快找到解(两层就到了)。不用像DFS一样找完一枝才一另一枝,万一左边的枝条很长呢?
于是我们可以得知BFS一个重要应用——找到最短路径。
这里BFS经典例题:迷宫。
迷宫有7*7个格子,格子为‘O’则可以通过,‘X’为路障不能通过,起点是‘B’,终点是‘E’,求‘B’到‘E’最小步数。注意不能走回头路。
代码:
#include结果 : 12
根据上述两个例题,我们可以有一个一般模板:
要返回值的类型 BFS(初始点数据){
初始化队列;
将初始点数据放入队列;
while(队列不为空)
{
取出队列首元素;
If(元素符合要求)
{ 结束,返回相关值 }
将元素的分支/周围元素加入到队列
将刚访问的元素标记。
}
}*
至此关于BFS的简单介绍到此结束,感谢阅读!