图的BFS和DFS算法
图
图是一种灵活的数据结构,一般作为一种模型用来定义对象之间的关系或联系。对象由顶点(V)表示,而对象之间的关系或者关联则通过图的边(E)来表示。
图可以分为有向图和无向图,一般用G=(V,E)来表示图。经常用邻接矩阵或者邻接表来描述一副图。
在图的基本算法中,最初需要接触的就是图的遍历算法,根据访问节点的顺序,可分为广度优先搜索(BFS)和深度优先搜索(DFS)。
广度优先搜索(BFS)
广度优先搜索在进一步遍历图中顶点之前,先访问当前顶点的所有邻接结点。
- 首先选择一个顶点作为起始结点,并将其染成灰色,其余结点为白色。
- 将起始结点放入队列中。
- 从队列首部选出一个顶点,并找出所有与之邻接的结点,将找到的邻接结点放入队列尾部,将已访问过结点涂成黑色,没访问过的结点是白色。如果顶点的颜色是灰色,表示已经发现并且放入了队列,如果顶点的颜色是白色,表示还没有发现
- 按照同样的方法处理队列中的下一个结点。
就是出队的顶点变成黑色,在队列里的是灰色,还没入队的是白色。
表示顶点的数据结构
function Vertex() {
if (!(this instanceof Vertex))
return new Vertex();
this.color = this.WHITE; //初始为 白色
this.pi = null; //初始为 无前驱
this.d = this.INFINITY; //初始为 无穷大
this.edges = null; //由顶点发出的所有边
this.value = null; //节点的值 默认为空
}
Vertex.prototype = {
constructor: Vertex,
WHITE: 'white', //白色
GRAY: 'gray', //灰色
BLACK: 'black', //黑色
INFINITY: null, //d 为 null 时表示无穷大
}
表示边的数据结构
function Edge() {
if (!(this instanceof Edge))
return new Edge();
this.index = null; //边所依附的节点的位置
this.sibling = null;
}
表示图的数据结构
function Graph() {
if (!(this instanceof Graph))
return new Graph();
this.graph = []; //存放顶点的数组
}
Graph.prototype = {
constructor: Graph,
addNode: function (node) {
this.graph.push(node);
},
getNode: function (index) {
return this.graph[index];
}
}
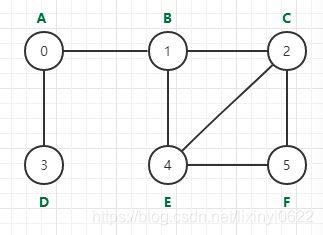
构建图
//创建 顶点
var vA = Vertex();
var vB = Vertex();
var vC = Vertex();
var vD = Vertex();
var vE = Vertex();
var vF = Vertex();
vA.value = 'A';
vB.value = 'B';
vC.value = 'C';
vD.value = 'D';
vE.value = 'E';
vF.value = 'F';
//构建由 A 节点发出的边集
var eA1 = Edge();
var eA2 = Edge();
eA1.index = 1;
eA2.index = 3;
eA1.sibling = eA2;
vA.edges = eA1;
//构建有 B 节点发出的边集
var eB1 = Edge();
var eB2 = Edge();
var eB3 = Edge();
eB1.index = 0;
eB2.index = 4;
eB3.index = 2;
eB1.sibling = eB2;
eB2.sibling = eB3;
vB.edges = eB1;
//构建由 C 节点发出的边
var eC1 = Edge();
var eC2 = Edge();
var eC3 = Edge();
eC1.index = 1;
eC2.index = 4;
eC3.index = 5;
eC1.sibling = eC2;
eC2.sibling = eC3;
vC.edges = eC1;
//构建由 D 节点发出的边
var eD1 = Edge();
eD1.index = 0;
vD.edges = eD1;
//构建由 E 节点发出的边
var eE1 = Edge();
var eE2 = Edge();
var eE3 = Edge();
eE1.index = 1;
eE2.index = 2;
eE3.index = 5;
eE1.sibling = eE2;
eE2.sibling = eE3;
vE.edges = eE1;
//构建由 F 节点发出的边
var eF1 = Edge();
var eF2 = Edge();
eF1.index = 2;
eF2.index = 4;
eF1.sibling = eF2;
vF.edges = eF1;
//构建图
var g = Graph();
g.addNode(vA);
g.addNode(vB);
g.addNode(vC);
g.addNode(vD);
g.addNode(vE);
g.addNode(vF);
广度优先搜索
function BFS(g, s) {
let queue = []; //辅助队列 Q
s.color = s.GRAY; //首次发现s涂为灰色
s.d = 0; //距离为0
queue.push(s); //将s放入队列 Q
while (queue.length > 0) { //当队列Q中有顶点时执行搜索
let u = queue.shift(); //将Q中的第一个元素移出
if (u.edges == null) continue; //如果从当前顶点没有发出边
let sibling = u.edges; //获取表示邻接边的链表的头节点
while (sibling != null) { //当链表不为空
let index = sibling.index; //当前边所连接的顶点在队列中的位置
let n = g.getNode(index); //获取顶点
if (n.color == n.WHITE) { //如果没有被访问过
n.color = n.GRAY; //涂为灰色
n.d = u.d + 1; //距离加1
n.pi = u; //设置前驱节点
queue.push(n); //将 n 放入队列 Q
}
sibling = sibling.sibling; //下一条边
}
u.color = u.BLACK; //当前顶点访问结束 涂为黑色
}
}
访问顺序
B->A->E->C->D->F
深度优先搜索(DFS)
深度优先搜索在搜索过程中访问某个顶点后,需要递归地访问此顶点的所有未访问过的相邻顶点。
深度优先搜索一般默认的源点有多个。
初始条件下所有节点为白色,选择一个作为起始顶点,按照如下步骤遍历:
- 选择起始顶点涂成灰色,表示还未访问
- 从该顶点的邻接顶点中选择一个,继续这个过程(即再寻找邻接结点的邻接结点),一直深入下去,直到一个顶点没有邻接结点了,涂黑它,表示访问过了
- 回溯到这个涂黑顶点的上一层顶点,再找这个上一层顶点的其余邻接结点,继续如上操作,如果所有邻接结点往下都访问过了,就把自己涂黑,再回溯到更上一层。
- 上一层继续做如上操作,知道所有顶点都访问过。
数据结构的表示上面,只有顶点的表示稍有不同,别的都一样。
function Vertex() {
if (!(this instanceof Vertex))
return new Vertex();
this.color = this.WHITE; //初始为 白色
this.pi = null; //初始为 无前驱
this.d = null; //时间戳 发现时
this.f = null; //时间戳 邻接链表扫描完成时
this.edges = null; //由顶点发出的所有边
this.value = null; //节点的值 默认为空
}
Vertex.prototype = {
constructor: Vertex,
WHITE: 'white', //白色
GRAY: 'gray', //灰色
BLACK: 'black', //黑色
}
深度优先搜索
function DFS(g) {
let t = 0; //时间戳
for (let v of g.vertexs) { //让每个节点都作为一次源节点
if (v.color == v.WHITE) DFSVisit(g, v);
}
function DFSVisit(g, v) {
t = t + 1; //时间戳加一
v.d = t;
v.color = v.GRAY;
let sibling = v.edges;
while (sibling != null) {
let index = sibling.index;
let n = g.getNode(index);
if (n.color == n.WHITE) {
n.pi = v;
DFSVisit(g, n); //先纵向找
}
sibling = sibling.sibling; //利用递归的特性来回溯
}
v.color = v.BLACK;
t = t + 1; //时间戳加一
v.f = t;
}
}
访问顺序
F->C->E->B->D->A