图_邻接表_图的深度优先遍历DFS_找到图中的所有路径_图的广度优先遍历BFS一编程小栗子
目录:
1.有向图
2.图的存储结构之邻接表
3.图的遍历-深度优先搜索遍历DFS:Depth First Search
3.1图的遍历-广度优先搜索遍历BFS:Breadth First Search
3.2深度优先遍历和广度优先遍历实现代码
4.DFS的一应用小例子
注意:图的遍历与找到图中的所有路径虽然是不同的问题,但只要稍微改变一下DFS深度优先遍历算法,即可完美解决找到图中的所有路径问题
问题提要:
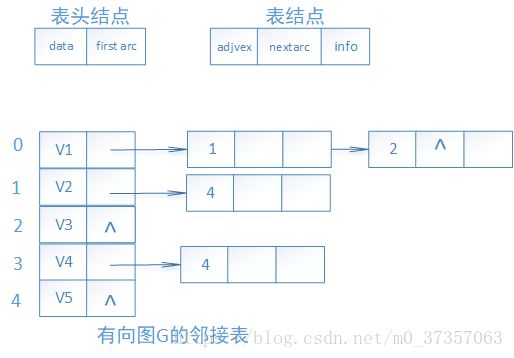
如下一有向图G:找到其所有路径:V1->V2->V5;V1->V3;V4->V5
1.有向图:
1.1图的存储结构之邻接矩阵
2.图的存储结构之邻接表
//用邻接表来存有向图
//先定义图的顶点数据结构,及存一个调用耗时
typedef struct NodeS
{
int num;
int time;
int visited;
}Node;
//有向图的邻接表表示,每个顶点对应一个列表
typedef struct ALGraphS{
vector vecNodes;
vector*> vexLists;//vector里存list的对象的指针
int vexNum, arcNum;
vector vexIn;//顶点的入度向量
}ALGraph;
/*像ALGraphS这样的只包含指针,不对指针所只资源进行管理的类(结构)的数据结构是很糟糕的数据结构!
应该将图定义成一个类,这个类包含构造函数(包括复制)构造函数,赋值=构造函数、析构函数等。
*/ Node类型结构存储:num:顶点编号(从0计起)
time(见下文题目),和visited(访问标识)visited=0表示没事访问过,visited=1表示访问过。
ALGraph:Adjacency List Graph结构类型存储:
vector
vector
int vexNum, arcNum;//vexNum:图中结点的个数;arcNum:图中边的条数
vector
3.图的遍历-深度优先遍历DFS
参考[1]严, 蔚敏, 吴, 伟民. 数据结构(C语言版)[J]. 计算机教育, 2012, No.168(12)。P169
bool visited[MAX]; //访问标志数组
Status(*VisitFunc)(int v); //函数变量
void DFSTraverse(Grahp G, Status(*Visit)(int v))
{//对图G做深度优先遍历
VisitFunc = Visit;
for (v = 0; v < G.vexnum; ++v) visited[v] = false;//访问标识数组初始化
for (v = 0; v < G.vexnum; ++v)
{
if (!visited[v]) DFS(G, v);//对尚未访问的顶点调用DFS
}
}
w=FirstAdjVec(G, v)//得到图G的顶点v的第一个邻接顶点w
NextAdjVex(G, v, w)//返回图G的顶点v中的在邻接点w之后的下一个邻接顶点
void DFS(Grahp, int v)
{
visited[v] = TRUE;
VisitFunc(v);//访问顶点v
for (w = FirstAdjVec(G, v); w >= 0; w=NextAdjVex(G,v,w))
{//对v的尚未访问的邻接顶点w递归调用DFS函数
if (!visited[w]) DFS(G, w);
}
}/*
遍历图的过程实质上是对每个顶点查找其邻接点的过程,
该过程耗费的时间取决于图所采用的存储结构
当用二维数组表示邻接矩阵作为图的存储结构时,
查找每个顶点的所有邻接顶点所需的时间为O(n*n)
n为图中的顶点数。
而当以邻接表作为图的存储结构时,找邻接点所需的
时间为O(e),e为无向图中边的数或有向图中弧的数,
所有当用邻接表作为存储结构时,深度优先搜索遍历图的
时间复杂度为O(n+e)
*/
3.1图的遍历-广度优先搜索遍历BFS:Breadth First Search
/*
图的广度优先遍历Breadth First Search
类似于树的按层次遍历
参考[1]参考[1]严, 蔚敏, 吴, 伟民. 数据结构(C语言版)[J]. 计算机教育, 2012, No.168(12)。P170
在遍历的过程中需要记录每个顶点有没有被访问过的标志数组,
我这里是在结点数据结构中设置了该标志位visited
typedef struct NodeS
{
int num;
int time;
int visited;
}Node;
为了能够顺次访问路径长度为2、3、...的顶点,需要附设队列以存储已经被访问的路径长度为1,2,3...的顶点。
每次从队列头取顶点(出队)并遍历该顶点的所有邻接顶点
如果该邻接顶点没有访问过,就置位其访问标志位,
并访问该顶点,然后将其入队
分析:每个顶点至多进队列一次。
遍历图的实质是通过边或弧找邻接点的过程,
因为广度优先遍历和深度优先遍历的时间复杂度相同O(n+e)
区别仅仅在于对顶点的访问顺序不同。
*/
viod BFSTraverse(Graph G, Status(*Visit)(int v))
{//按广度优先非递归遍历图G,使用辅助队列Q和访问标志数组visited
for (int v = 0; v < G.vexnum; v++) visited[v] = false;
InitQueue(Q);//初始化空的辅助队列Q
for (int v = 0; v < G.vexnum; v++)
{
if (!visited[v])//v尚未访问
{
visited[v] = true;
Visit(v);
EnQueue(Q, v); //v入队
while (!QueueEmpty(Q))
{
DeQueue(Q, u); //队头元素出对并设置为u
for (int w = FirstAdjVex(G, u); w >= 0; w=NextAdjVex(G,u,w))
{//w为顶点u的尚未访问的邻接顶点
/*
FirstAdjVex(G, u)返回图G的顶点u的第一个邻接顶点
NextAdjVex(G,u,w)返回图G的顶点u的邻接顶集合中在邻接顶w之后的一个邻接顶点
*/
if (!visited[w])
{
visited[w] = true;
Visit(w);
EnQueue(Q, w);//
}
}
}
}
}
}
3.2深度优先遍历和广度优先遍历实现代码
再生成一个二叉树
变成只有一个根节点的有向图,来测试图的广度优先遍历,和深度优先遍历:
V1->V2
V2->V3
V2->V4
V4->V5
V4->V6
V5->V7
7个顶点、6条有向边
就假设每个顶点存储的值为1吧
7 6
1
1
1
1
1
1
1
1 2
2 3
2 4
4 5
4 6
5 7
广度优先遍历输出:1 2 3 4 5 6 7
深度优先遍历输出:1 2 3 4 5 7 6
图结点和邻接表数据结构定义为:
//用邻接表来存有向图
//先定义图的顶点数据结构,及存一个调用耗时
typedef struct NodeS
{
int num;
int time;
int visited;
}Node;
//有向图的邻接表表示,每个顶点对应一个列表
typedef struct ALGraphS{
vector vecNodes;//图的结点地址向量,依次存每一个结点的地址
vector*> vexLists;//存储图中有向边的信息:每个顶点有一个邻接表,该邻接表上依次挂有其邻接顶点的地址
int vexNum, arcNum;
vector vexIn;//顶点的入度向量
}ALGraph;
/*像ALGraphS这样的只包含指针,不对指针所只资源进行管理的类(结构)的数据结构是很糟糕的数据结构!
应该将图定义成一个类,这个类包含构造函数(包括复制)构造函数,赋值=构造函数、析构函数等。
*/ 3.2.1深度优先遍历实现代码:
void DFS(ALGraph& al, int v)
{//从图al的顶点v出发,递归地深度优先遍历图G
al.vecNodes[v]->visited = 1;
cout << v + 1 << " ";
for (int i = 1; i < (al.vexLists[v]->size()); i++)
{
int nodeNum = al.vexLists[v]->at(i)->num;
if (al.vecNodes[nodeNum]->visited == 0)
{
DFS(al, nodeNum);
}
}
}
void DFSTraverse(ALGraph& al)
{
for (int i = 0; i < al.vexNum; i++)
{
if (al.vecNodes[i]->visited == 0)
{
DFS(al, i);
}
}
/*
algraph是在堆中分配的结点,每次范围后,其每一个结点的标志位都设置为1了,退出时,
下次再遍历前要清一下标志位。
*/
for (int i = 0; i < al.vexNum; i++)
{
al.vecNodes[i]->visited = 0;
}
}3.2.2广度优先遍历实现代码:
/*
图的广度优先遍历Breadth First Search
类似于树的按层次遍历过程:
*/
void BFSTraverse(ALGraph& al)
{
queue nodeQueue;
for (int v = 0; v < al.vexNum; v++)
{
if (al.vecNodes[v]->visited == 0)
{
al.vecNodes[v]->visited = 1;
cout << al.vecNodes[v]->num +1<< " ";//访问第i个结点
nodeQueue.push(v);//v入队
while (!nodeQueue.empty())
{
int u = nodeQueue.front();
nodeQueue.pop();//队头元素出队,并赋值给u
for (int w = 1; w < (al.vexLists[u]->size()); w++)
{
int nodeNum = al.vexLists[u]->at(w)->num;
if (al.vecNodes[nodeNum]->visited == 0)
{
al.vecNodes[nodeNum]->visited = 1;
cout << nodeNum +1<< " ";
nodeQueue.push(nodeNum);
}
}
}
}
}
/*
algraph是在堆中分配的结点,每次范围后,其每一个结点的标志位都设置为1了,退出时,
下次再遍历前要清一下标志位。
*/
for (int i = 0; i < al.vexNum; i++)
{
al.vecNodes[i]->visited = 0;
}
} 测试例子:
#include "stdafx.h"
#include
#include
#include
#include
using namespace std;
//用邻接表来存有向图
//先定义图的顶点数据结构,及存一个调用耗时
typedef struct NodeS
{
int num;
int time;
int visited;
}Node;
//有向图的邻接表表示,每个顶点对应一个列表
typedef struct ALGraphS{
vector vecNodes;//图的结点地址向量,依次存每一个结点的地址
vector*> vexLists;//存储图中有向边的信息:每个顶点有一个邻接表,该邻接表上依次挂有其邻接顶点的地址
int vexNum, arcNum;
vector vexIn;//顶点的入度向量
}ALGraph;
/*像ALGraphS这样的只包含指针,不对指针所只资源进行管理的类(结构)的数据结构是很糟糕的数据结构!
应该将图定义成一个类,这个类包含构造函数(包括复制)构造函数,赋值=构造函数、析构函数等。
*/
int _tmain(int argc, _TCHAR* argv[])
{
ALGraph algraph;
cin >> algraph.vexNum;
cin >> algraph.arcNum;
//algraph.visited = new vector(algraph.vexNum,0);
//fill(algraph.visited->begin(), algraph.visited->end(), 0);
for (int i = 0; i < algraph.vexNum; i++)
{
int time;
cin >> time;
Node* vexptr = new Node;
vexptr->time = time;
vexptr->num = i;
vexptr->visited = 0;
algraph.vecNodes.push_back(vexptr);
vector* vexVec = new vector < Node* > ;
vexVec->push_back(vexptr);
algraph.vexLists.push_back(vexVec);
//顶点的入度向量
algraph.vexIn.push_back(0);
}
int Vex1, Vex2;
for (int i = 0; i < algraph.arcNum; i++)
{
cin >> Vex1 >> Vex2;
algraph.vexLists[Vex1-1]->push_back(algraph.vecNodes[Vex2-1]);
//顶点的入度统计
algraph.vexIn[Vex2-1]++;
}
cout << "深度优先遍历:" << endl;
DFSTraverse(algraph);
cout << endl;
/*
algraph是在堆中分配的结点,每次范围后,其每一个结点的标志位都设置为1了,在遍历前要清一下标志位。
*/
cout << "广度优先遍历:" << endl;
BFSTraverse(algraph);
//释放图所占用的内存空间:将那些new出来的,在堆区分配的空间删除一下,养成良好的编程习惯!
//最好的办法是使用智能指针,对这些对象进行引用计数,让系统帮我们回收
for (int i = 0; i < algraph.vecNodes.size(); i++)
{
delete algraph.vecNodes[i];
algraph.vecNodes[i] = nullptr;
}
/*真正new出来的对象实体是Node结点,邻接表存从只是Node对象的地址而已!*/
for (int i = 0; i < algraph.vexLists.size(); i++)
{
algraph.vexLists[i]->clear();//将指针向量清空。
delete algraph.vexLists[i];
}
system("pause");
return 0;
}
输入输出:
输入
7 6
1
1
1
1
1
1
1
1 2
2 3
2 4
4 5
4 6
5 7
输出:
深度优先遍历:
1 2 3 4 5 7 6
广度优先遍历:
1 2 3 4 5 6 7 请按任意键继续. . .
4.DFS的一应用小例子
/*
参考:
https://blog.csdn.net/m0_38059843/article/details/81080999
今天我们看到的阿里巴巴提供的任何一项服务后边都有着无数子系统和组件的支撑,子系统之间也互相依赖关联,
其中任意一个环节出现问题都可能对上游链路产生影响。小明做为新人接收到的第一个任务就是去梳理所有的依赖关系,
小明和每个系统的负责人确认了依赖关系,记录下调用对应系统的耗时,用这些数据分析端到端链路的数目和链路上最长的耗时。
输入: 小明搜集到的系统耗时和依赖列表
5 4 // 表示有5个系统和 4个依赖关系
3 // 调用1号系统耗时 3 ms
2 // 调用2号系统耗时 2 ms
10 // 调用3号系统耗时 10 ms
5 // 调用4号系统耗时 5 ms
7 // 调用5号系统耗时 7 ms
1 2 // 2号系统依赖1号系统
1 3 // 3号系统依赖1号系统
2 5 // 5号系统依赖2号系统
4 5 // 5号系统依赖4号系统
5 4
3
2
10
5
7
1 2
1 3
2 5
4 5
输出: 调用链路的数目 和最大的耗时, 这里有三条链路1->2->5,1->3, 4->5,最大的耗时是1到3的链路 3+10 = 13,无需考虑环形依赖的存在。
3 13
思路:
1、有向图的遍历。图的存储用的是邻接表表示法,找出入度为0的点(根节点),然后dfs,将路径保存在一个二维的vector中,vector的size即为链路的数目,然后找出耗时最大的那一条。
2、评论有个老哥说可以用multimap来解决,才学疏浅以前确实没有用过0.0,学习了。
3、如果有环怎么办?有环也不用怕,dfs的时候判断一下下一个结点是否是根节点,是就结束,不是就继续。
https://blog.csdn.net/m0_38059843/article/details/81080999
*/
4.1首先以邻接表的形式定义图的存储结构:
ALGraphS数据结构有点复杂,好好梳理一下!
#include "stdafx.h"
#include
#include
#include
#include
using namespace std;
vector > paths;//存储所有路径的二维向量
vector path;//存储单条路径
//用邻接表来存有向图
//先定义图的顶点数据结构,及存一个调用耗时
typedef struct NodeS
{
int num;
int time;
int visited;
}Node;
//有向图的邻接表表示,每个顶点对应一个列表
typedef struct ALGraphS{
vector vecNodes;
vector*> vexLists;//vector里存list的对象的指针
int vexNum, arcNum;
vector vexIn;//顶点的入度向量
}ALGraph;
/*像ALGraphS这样的只包含指针,不对指针所只资源进行管理的类(结构)的数据结构是很糟糕的数据结构!
应该将图定义成一个类,这个类包含构造函数(包括复制)构造函数,赋值=构造函数、析构函数等。
*/
4.2在邻接表存储结构的形式上实现图的深度优先遍历(递归dfs函数)
getPaths()函数得图中所有的路径
void dfs(ALGraph& al, int v)
{//注意:顶点编号从0计起,所以说第一个顶点V1的下标是0
/*这个函数的注意两点就是对顶点编号的压栈、退栈、以及对访问节点的设置visited标志位和撤销visited标志位*/
/*关键就是以栈的形式对递归调用的过程加以完美描述!*/
path.push_back(v);
if (al.vexLists[v]->size() == 1)//这里等同于判断v顶点的出度为0,
{
paths.push_back(path);
}
else
{
for (int i = 1; i < (al.vexLists[v]->size()); i++)
{
int nodeNum = al.vexLists[v]->at(i)->num;
if (al.vecNodes[nodeNum]->visited == 0 )
{
al.vecNodes[nodeNum]->visited = 1;
dfs(al, nodeNum);
al.vecNodes[nodeNum]->visited = 0;
}
}
}
path.pop_back();
return;
}
void getPaths(ALGraph& al)
{
for (int i = 0; i < al.vexNum; i++)
{
if (al.vexIn[i] == 0)
{//对入度为0的顶点进行深度优先遍历
dfs(al, i);
}
}
}测试示例:
int _tmain(int argc, _TCHAR* argv[])
{
ALGraph algraph;
cin >> algraph.vexNum;
cin >> algraph.arcNum;
//algraph.visited = new vector(algraph.vexNum,0);
//fill(algraph.visited->begin(), algraph.visited->end(), 0);
for (int i = 0; i < algraph.vexNum; i++)
{
int time;
cin >> time;
Node* vexptr = new Node;
vexptr->time = time;
vexptr->num = i;
vexptr->visited = 0;
algraph.vecNodes.push_back(vexptr);
vector* vexVec = new vector < Node* > ;
vexVec->push_back(vexptr);
algraph.vexLists.push_back(vexVec);
//顶点的入度向量
algraph.vexIn.push_back(0);
}
int Vex1, Vex2;
for (int i = 0; i < algraph.arcNum; i++)
{
cin >> Vex1 >> Vex2;
algraph.vexLists[Vex1-1]->push_back(algraph.vecNodes[Vex2-1]);
//顶点的入度统计
algraph.vexIn[Vex2-1]++;
}
//DFSTraverse(algraph);
getPaths(algraph);
int maxTime=0;
int time=0;
for (int i = 0; i < paths.size(); i++)
{
for (int j = 0; j < paths[i].size(); j++)
{
//cout << paths[i][j] << " ";
time += (algraph.vecNodes[paths[i][j]]->time);
}
if (time > maxTime)
{
maxTime = time;
}
time = 0;
}
cout << paths.size() << " " << maxTime;
//释放图所占用的内存空间:将那些new出来的,在堆区分配的空间删除一下,养成良好的编程习惯!
//最好的办法是使用智能指针,对这些对象进行引用计数,让系统帮我们回收
for (int i = 0; i < algraph.vecNodes.size(); i++)
{
delete algraph.vecNodes[i];
algraph.vecNodes[i] = nullptr;
}
/*真正new出来的对象实体是Node结点,邻接表存从只是Node对象的地址而已!*/
for (int i = 0; i < algraph.vexLists.size(); i++)
{
algraph.vexLists[i]->clear();//将指针向量清空。
delete algraph.vexLists[i];
}
system("pause");
return 0;
}
输入:
5 4
3
2
10
5
7
1 2
1 3
2 5
4 5
输出:
3 13
数据结构 图 图的深度优先遍历DFS 找到图中的所有路径 编程例子