bzoj 1856 //1856: [Scoi2010]字符串 dp动归/卡特兰数
bzoj 1856 //1856: [Scoi2010]字符串 //在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1856
更多题解,详见https://blog.csdn.net/mrcrack/article/details/90228694BZOJ刷题记录
1.dp动归
//1856: [Scoi2010]字符串
//在线测评地址https://www.lydsy.com/JudgeOnline/problem.php?id=1856
//样例2 2解释如下
//所有可能1100,1010,1001,0011,0101,0110
//不可能1001,0011,0101,0110
//确定的情况1100,1010
//dp(动归)参考此文https://www.luogu.org/problemnew/solution/P1641?page=4 作者: UKE_Automaton 更新时间: 2018-04-02 16:00
//f[i][j] i个1,j个0对应的方案数
//f[i][j]=f[i-1][j]+f[i][j-1]
//f[i-1][j]串尾补1 ==> f[i][j]
//f[i][j-1]串尾补0 ==> f[i][j]
//f[i][j]=f[i-1][j]+f[i][j-1]模拟如下,希望能通过模拟,看懂dp.2019-9-17
/*
1 0
1 f[1][0]=1
1 1
10 f[1][1]=f[1][0]+f[0][1]=1+0=1
2 1
110 101 f[2][1]=f[2][0]+f[1][1]=1+1=2 11=>110,10=>101
2 2
1100 1010 f[2][2]=f[2][1]+f[1][2]=2+0=2 110=>1100,101=>1010
3 1
1110 1101 1011 f[3][1]=f[3][0]+f[2][1]=1+2=3 111=>1110 110=>1101 101=>1011
*/
//此处https://www.luogu.org/problem/P1641提交dp代码,30分,测试点1-3AC.
#include
#include
#define LL long long
#define maxn 1010
#define mod 20100403
LL f[maxn][maxn];
int main(){
int n,m,i,j;
scanf("%d%d",&n,&m);
memset(f,0,sizeof(f));
for(i=1;i<=n;i++)f[i][0]=1;
for(i=1;i<=n;i++)
for(j=1;j<=i;j++)
f[i][j]=(f[i-1][j]+f[i][j-1])%mod;
printf("%lld\n",f[n][m]);
return 0;
}
2.卡特兰数
//此文https://www.cnblogs.com/Essein/p/9734846.html思路很棒,摘抄如下
为什么要以y=-1作为对称轴呢,读者可以多画几副图,非法情况,一定是从(0,-2)出发,到达(n+m,n-m),中间不会出现线段的断裂。
//此文https://www.cnblogs.com/jianglangcaijin/p/3443689.html推导特别好,摘抄如下
(0,-2)->(n+m,n-m)计算出的方案,与(0,0)->(n+m,n-m)中的非法方案一一对应.故可抛开(0,0)->(n+m,n-m),直接(0,-2)->(n+m,n-m)计算出的方案作为非法方案.2019-9-17 20:53
2.1快速幂+乘法逆元
| 820 kb | 488 ms |
//快速幂+乘法逆元
//此文https://www.cnblogs.com/cjyyb/p/9837037.html代码写得不错
//样例通过,提交AC.2019-9-17 21:36
#include
#define LL long long
#define mod 20100403
LL quick_pow(LL a,LL n){
LL ans=1;
while(n){
if(n&1)ans=ans*a%mod;//此处错写成if(a&1)ans=ans*a%mod;,够昏
a=a*a%mod;
n/=2;
}
return ans;
}
LL C(LL n,LL m){//n!/((n-m)!m!)=n*(n-1)*(n-2)*...*(m+1)/(n-m)!
LL a=1,b=1,i;
for(i=n;i>m;i--)a=a*i%mod;
for(i=n-m;i>=1;i--)b=b*i%mod;
return a*quick_pow(b,mod-2)%mod;
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
printf("%lld\n",(C(n+m,m)-C(n+m,m-1)+mod)%mod);
return 0;
}
2.2扩展欧几里德算法+逆元
| 820 kb | 484 ms |
//扩展欧几里德算法+逆元
//在纸上推了一遍 扩展欧几里德算法
//扩展欧几里德算法 编写完成后,不放心,又简单测试了。
//样例通过,提交AC.
//惊叹,第一次用 扩展欧几里德算法 求逆元,没想到,一次成功。2019-9-18
//推导过程如下
/*
ax+by=1
(1)ax+by=gcd(a,b)
bx'+a%by'=gcd(b,a%b)
bx'+(a-a/b*b)y'=gcd(b,a%b)
bx'+ay'-a/b*b*y'=gcd(b,a%b)
(2)ay'+b(x'-a/b*y')=gcd(b,a%b)
对比(1)、(2)可得
x=y',y=x'-a/b*y'
*/
#include
#define LL long long
#define mod 20100403
void exgcd(LL a,LL b,LL *x,LL *y){//扩展欧几里德算法 求逆元 ax%b=1 => (ax-1)=by => ax+by=1,x是a的逆元
LL t;
if(b==0){
*x=1,*y=0;
return;
}
exgcd(b,a%b,x,y);
t=*x,*x=*y,*y=t-a/b**y;
}
LL C(LL n,LL m){
LL c=1,a=1,i,x,y;
for(i=n;i>m;i--)c=c*i%mod;
for(i=n-m;i>=1;i--)a=a*i%mod;
exgcd(a,mod,&x,&y);
x=(x%mod+mod)%mod;
return c*x%mod;
}
int main(){
int n,m;
scanf("%d%d",&n,&m);
printf("%lld\n",(C(n+m,m)-C(n+m,m-1)+mod)%mod);
return 0;
}
![bzoj 1856 //1856: [Scoi2010]字符串 dp动归/卡特兰数_第1张图片](http://img.e-com-net.com/image/info8/4b1b4fb6bfbb4790a2bff8d4ab0b01dd.jpg)
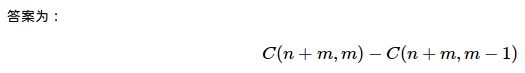
![bzoj 1856 //1856: [Scoi2010]字符串 dp动归/卡特兰数_第2张图片](http://img.e-com-net.com/image/info8/5166936748894f14a4f45d1e19664227.jpg)