图的遍历之广度优先遍历BFS

GraphBasicOperation.cpp文件链接：https://blog.csdn.net/qq_16261421/article/details/106005857

广度优先搜索遍历的过程是：

　　（1）访问初始点v，接着访问v的所有未被访问过的邻接点v1，v2，…，vt。

　　（2）按照v1，v2，…，vt的次序，访问每一个顶点的所有未被访问过的邻接点。　　　

　　（3）依次类推，直到图中所有和初始点v有路径相通的顶点都被访问过为止。  

　广度优先遍历体现先进先出的特点，用队列实现。    

　以邻接表为存储结构，用广度优先搜索遍历图时，需要使用一个队列，以类似于按层次遍历二叉树遍历图。对应的算法如下（其中，v是初始顶点编号）：

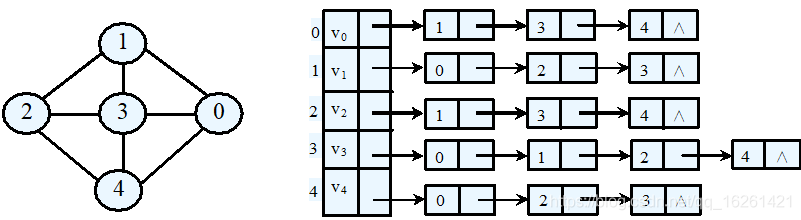
例如，以上图的邻接表为例调用BFS()函数，假设初始顶点编号v=2，给出调用BFS()的执行过程。 

代码实现如下:

#include "GraphBasicOperation.cpp"
void BFS(ALGraph *G,int v)  
{
	ArcNode *p;
	int queue[MAXV],front=0,rear=0;			//定义循环队列并初始化
	int visited[MAXV];            			//定义存放结点的访问标志的数组
	int w,i;
	for (i=0;in;i++) visited[i]=0;		//访问标志数组初始化
	printf("%2d",v); 						//输出被访问顶点的编号
	visited[v]=1;              				//置已访问标记
	rear=(rear+1)%MAXV;
	queue[rear]=v;             				//v进队
	while (front!=rear)       				//若队列不空时循环
	{	
		front=(front+1)%MAXV;
		w=queue[front];       				//出队并赋给w
		p=G->adjlist[w].firstarc; 			//找与顶点w邻接的第一个顶点
		while (p!=NULL) 
		{	
			if (visited[p->adjvex]==0) 		//若当前邻接顶点未被访问
			{
				printf("%2d",p->adjvex);  	//访问相邻顶点
				visited[p->adjvex]=1;		//置该顶点已被访问的标志
				rear=(rear+1)%MAXV;			//该顶点进队
				queue[rear]=p->adjvex;
           	}
           	p=p->nextarc;              		//找下一个邻接顶点
		}
	}
	printf("\n");
}
void main()
{
	int i,j;
	MGraph g;
	ALGraph *G;
	int A[MAXV][5]={
		{0,1,0,1,1},
		{1,0,1,1,0},
		{0,1,0,1,1},
		{1,1,1,0,1},
		{1,0,1,1,0}};
	g.n=5;g.e=16;
	for (i=0;i