数据结构的连通性问题
连通性问题,这可真是tarjan的天下啊,不过这篇文章并没有打算扯到tarjan的起源模型强连通分量,主要还是说说自己对其它连通性问题的思考,所以,如果你还不会tarjan算法的话,嗯,点这里:byvoid的tarjan算法讲解 膜拜一下神牛。
当然了,关于连通性问题这里还有:byvoid的连通性问题讲解 再次膜拜。这篇文章是自己将三篇研究日记汇总而成的,所以中间有一部分属于含有错误的,标题已经进行了警示,大家也可以找找看为什么不对,文章后面进行了订正与说明,好的,进入正题。
基本概念:
1、连通:两个点之间存在若干条边将其连接,称其连通
2、强连通:有向图中的两点可以互达(A→B 并且 B→A),称其强连通3、弱连通:有向图中的两点可以到达(A→B 或者 B→A),称其弱连通
4、连通图:图G中任意两点都连通,则G为连通图
5、强连通图:有向图G中任意两点都强连通,则G为强连通图
6、弱连通图:有向图G中任意两点都弱连通,则G为弱连通图
7、强连通分量:非强连通图的极大强连通子图,称为强连通分量(极大指不能再大,与最大的意义不同)
8、点连通度:使无向图G不连通的最少删点数量为其点连通度
9、边连通度:使无向图G不连通的最少删边数量为其边连通度
10、点双连通图:点连通度大于1的无向图
11、边双连通图:边连通度大于1的无向图
12、双连通图:点连通度和边连通度均大于1的无向图
13、点双连通分量:非点双连通图的极大点双连通子图
14、边双连通分量:非边双连通图的极大边双连通子图
15、双连通分量:非双连通图的极大双连通子图
16、割点:点连通度为1的无向图中,被删除后将导致原图不连通的点
17、桥:边连通度为1的无向图中,被删除后将导致原图不连通的边
18、返祖边:在DFS中连接当前点与未访问完毕的点之间的边
19、横叉边:在DFS中连接当前点与已访问完毕的点之间的边
20、后向边:就是在DFS中,子孙指向祖先的边。
双连通分量:
双连通分量有两种:点双连通分量、边双连通分量。那双连通分量又是什么?到底是点的还是边的?这样不清楚的表述屡见不鲜,参考了众多人的博客后,关于双连通分量的定义,还是确定不下来,主要有以下几种说法:
1、指点双连通,与块同义2、指边双连通
3、有时指点双连通,有时指边双连通
4、满足点双连通或者边双连通
5、同时满足点双连通与边双连通
关于双连通的定义,众说纷纭,我觉得还是不要盲目相信任何人,毕竟说清楚是点双连通还是边双连通并没有碍多少事,那么以后就说清楚为好,免得出现歧义。
关系:
算法:
用dfn表示时间戳,用low表示简单环内的最小时间戳
强连通分量:当dfn[u] == low[u]
桥:当dfn[u] < low[v]
割点:当dfn[u] <= low[v]
这又从算法的角度印证了上面的结论:有桥则一定有割点,但是有割点不一定有桥,因为该点可以是环内搜索树的根节点,当没有该点的时候,环上各点将与该点的搜索树祖先节点不连通,但是若消去环上一边,环上各点与该点依然连通,这意味着它们与该点的祖先节点依然连通。
横叉边:
横叉边是一个定义在有向图搜索树中的概念,对于无向图它是没有任何意义的。有向图出现横叉边的原因是u→v不可行,然后u已经退栈成功,然而v→u可行,所以会访问到已经退栈的节点,这样的边称之为横叉边,然而在无向图中,这样的情况是不可能出现的,如果u→v是可行的,那么v→u也是可行的,因为无向图中的边是没有方向的,那么,在求无向图相关的桥、割点、点双连通分量、边双连通分量的时候,就不需要开一个布尔数组来记录该点是否访问完毕,即是否还在栈中,并且,也不需要开布尔数组来记录该点是否已经访问过,因为访问过的点dfn <> 0,据此可知,在无向图的连通求解中,可以不开任何布尔数组,切记切记!!
有向图强连通分量 Tarjan算法
[有向图强连通分量]
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。
[Tarjan算法]
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
算法伪代码如下
tarjan(u)
{
DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值
Stack.push(u) // 将节点u压入栈中
for each (u, v) in E // 枚举每一条边
if (v is not visted) // 如果节点v未被访问过
tarjan(v) // 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S) // 如果节点v还在栈内
Low[u] = min(Low[u], DFN[v])
if (DFN[u] == Low[u]) // 如果节点u是强连通分量的根
repeat
v = S.pop // 将v退栈,为该强连通分量中一个顶点
print v
until (u== v)
}
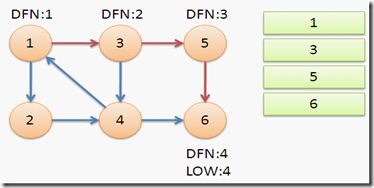
接下来是对算法流程的演示。
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
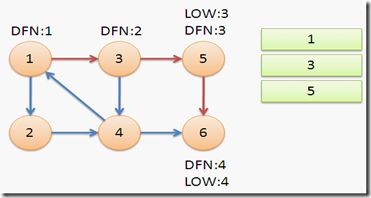
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
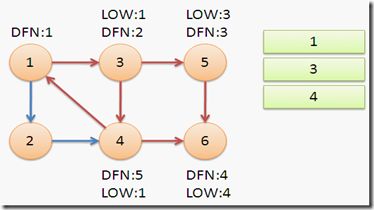
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。
至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。
可以发现,运行Tarjan算法的过程中,每个顶点都被访问了一次,且只进出了一次堆栈,每条边也只被访问了一次,所以该算法的时间复杂度为O(N+M)。
tarjan算法的简单证明:
针对tarjan的操作规则来讲解这个算法
其实,tarjan算法的基础是DFS。我们准备两个数组Low和Dfn。Low数组是一个标记数组,记录该点所在的强连通子图所在搜索子树的根节点的Dfn值(很绕嘴,往下看你就会明白),Dfn数组记录搜索到该点的时间,也就是第几个搜索这个点的。根据以下几条规则,经过搜索遍历该图(无需回溯)和对栈的操作,我们就可以得到该有向图的强连通分量。
- 数组的初始化:当首次搜索到点p时,Dfn与Low数组的值都为到该点的时间。
- 堆栈:每搜索到一个点,将它压入栈顶。
- 当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’不在栈中,p的low值为两点的low值中较小的一个。
- 当点p有与点p’相连时,如果此时(时间为dfn[p]时)p’在栈中,p的low值为p的low值和p’的dfn值中较小的一个。
- 每当搜索到一个点经过以上操作后(也就是子树已经全部遍历)的low值等于dfn值,则将它以及在它之上的元素弹出栈。这些出栈的元素组成一个强连通分量。
- 继续搜索(或许会更换搜索的起点,因为整个有向图可能分为两个不连通的部分),直到所有点被遍历。
由于每个顶点只访问过一次,每条边也只访问过一次,我们就可以在O(n+m)的时间内求出有向图的强连通分量。但是,这么做的原因是什么呢?
Tarjan算法的操作原理如下:
- Tarjan算法基于定理:在任何深度优先搜索中,同一强连通分量内的所有顶点均在同一棵深度优先搜索树中。也就是说,强连通分量一定是有向图的某个深搜树子树。
- 可以证明,当一个点既是强连通子图Ⅰ中的点,又是强连通子图Ⅱ中的点,则它是强连通子图Ⅰ∪Ⅱ中的点。
- 这样,我们用low值记录该点所在强连通子图对应的搜索子树的根节点的Dfn值。注意,该子树中的元素在栈中一定是相邻的,且根节点在栈中一定位于所有子树元素的最下方。
- 强连通分量是由若干个环组成的。所以,当有环形成时(也就是搜索的下一个点已在栈中),我们将这一条路径的low值统一,即这条路径上的点属于同一个强连通分量。
- 如果遍历完整个搜索树后某个点的dfn值等于low值,则它是该搜索子树的根。这时,它以上(包括它自己)一直到栈顶的所有元素组成一个强连通分量。
求有向图的强连通分量还有一个强有力的算法,为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法,其时间复杂度也是O(N+M)。与Trajan算法相比,Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS,不用建立逆图,更简洁。在实际的测试中,Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外,该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法,也有助于深入理解求双连通分量的Tarjan算法,两者可以类比、组合理解。
求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法,以及求最近公共祖先的离线Tarjan算法,在此对Tarjan表示崇高的敬意。
#include "cstdlib"
#include "cctype"
#include "cstring"
#include "cstdio"
#include "cmath"
#include "algorithm"
#include "vector"
#include "string"
#include "iostream"
#include "sstream"
#include "set"
#include "queue"
#include "stack"
#include "fstream"
//#include "strstream"
using namespace std;
#define M 2000 //题目中可能的最大点数
int STACK[M],top=0; //Tarjan 算法中的栈
bool InStack[M]; //检查是否在栈中
int DFN[M]; //深度优先搜索访问次序
int Low[M]; //能追溯到的最早的次序
int ComponetNumber=0; //有向图强连通分量个数
int Index=0; //索引号
vector Edge[M]; //邻接表表示
vector Component[M]; //获得强连通分量结果
void Tarjan(int i)
{
int j;
DFN[i]=Low[i]=Index++;
InStack[i]=true;
STACK[++top]=i;
for (int e=0;e // virtualDestruction.cpp : 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include
#include
#include
#include
//#include <>
using namespace std;
#define M 2000
vector Edge[M];//邻接表
vector res[M];//强连通分量
int componentNum=0;//强连通分量个数
int dfn[M];//每个点的遍历次序
int index=0;//次序索引
int low[M];//该点所在强连通分量所在搜索树的根节点次序号
stack seq;//遍历的点
bool inStack[M];
void tarjan(int i)
{
dfn[i]=low[i]=index++;
seq.push(i);
inStack[i]=true;
for (int j=0;jlow
}
if (dfn[i]==low[i])
{
int k=i;
componentNum++;
do
{
inStack[i]=false;
k=seq.top();
res[componentNum-1].push_back(k);
seq.pop();
}while(i!=k);
}
}
int _tmain(int argc, _TCHAR* argv[])
{
int N=6;
Edge[0].push_back(2);Edge[0].push_back(1);
Edge[1].push_back(3);
Edge[2].push_back(4);Edge[2].push_back(3);
Edge[3].push_back(0);Edge[3].push_back(5);
Edge[4].push_back(5);
memset(dfn,-1,sizeof(dfn));
memset(low,-1,sizeof(low));
memset(inStack,0,sizeof(inStack));
for(int i=0;i 下面是算法的一个模板:
#include
#include
#include
//从顶点0开始
// 要用的话要初始化:调用Adj.initial 和 tarjan.initial
//要解决问题用调用tarjan.solve
//对tarjan.initial要传入的参数是图边集Adj,和顶点个数n
const int maxn = 11000;
//顶点的规模
const int maxm = 210000;
//边的规模,如果是无向图要记得乘以2
const int GRAY = 0;
const int WHITE =-1;
const int BLACK = 1;
typedef struct Edge{
int s;
int e;
int next;
}Edge;
typedef struct Adj{
int edge_sum;
int head[maxn];
Edge edge[maxm];
void initial(){
edge_sum = 0;
memset(head,-1,sizeof(head));
}
void add_edge(int a, int b){
edge[edge_sum].s = a;
edge[edge_sum].e = b;
edge[edge_sum].next = head[a];
head[a] = edge_sum++;
}
}Adj;
typedef struct Tanjan{
int n;
int *head;
Adj *adj;
Edge *edge;
int cnt;
int top;
int cur;
int dfn[maxn];
int low[maxn];
int color[maxn];
int stack[maxn];
int belong[maxn];
void initial(Adj *_adj,int _n){
n = _n;
adj = _adj;
head = (*adj).head;
edge = (*adj).edge;
}
void solve(){
memset(dfn,-1,sizeof(dfn));
memset(color,WHITE,sizeof(color));
top = cnt = cur = 0;
for(int i = 0; i < n; i++)
if(color[i] == WHITE)//找到一个白色的顶点,就开始处理
tarjan(i);
}
inline int min(int a, int b){
if(a < b) return a;
else return b;
}
void tarjan(int i){
int j = head[i];
color[i] = GRAY;//标记为灰色
stack[top++] = i;//把结点圧入栈顶
dfn[i] = low[i] = ++cur;//给结点一个时间戳,并给Low初始化
while(j != -1){
int u = edge[j].e;
if (dfn[u] == WHITE){
tarjan(u);
low[i] = min(low[i],low[u]);
//更新low
}else if (color[u] == GRAY)
low[i] = min(low[i],dfn[u]);
//一条后向边
j = edge[j].next;
}
color[i] = BLACK;
if(low[i] == dfn[i]){
do{
j = stack[--top];
belong[j] = cnt;
}while(i != j);
++cnt;
}
}
}Tarjan;
Adj adj;
Tarjan tj; http://lib.csdn.net/article/datastructure/10310
http://www.cppblog.com/sosi/archive/2010/09/26/127797.aspx
http://blog.csdn.net/nothi/article/details/7739741
http://blog.csdn.net/e6894853/article/details/7898185
http://blog.csdn.net/xinghongduo/article/details/6195337