AtCoder Beginner Contest 163 solution

前言

我对官方的spj或是其他原因导致的第一题的IE有一点不满------浪费了我十几分钟.

这次E,F比赛时又没做出来,做DP不太成熟啦~

$A$

样例已经给你一个较精确的值了.

#include
using namespace std;
int main() {
	double n; scanf("%lf",&n);
	printf("%.5lf",n*6.28318530717958623200); 
	return 0;
}

$B$

int n,m,s;

int main() {
	qr(n); qr(m);
	for(int i=1,x;i<=m;i++)
		qr(x),s+=x;
	if(n<s) puts("-1");
	else pr2(n-s);
	return 0;
}

$C$

int n,d[N];

int main() {
	qr(n);
	for(int i=2,x;i<=n;i++)
		qr(x),d[x]++;
	for(int i=1;i<=n;i++) pr2(d[i]);
	return 0;
}

$D$

读者自推不难.

ll n,m,s[N],ans;

int main() {
	qr(n); qr(m); n++;
	for(int i=1;i<=n;i++) {
		s[i]=(s[i-1]+i)%mod;
		if(i>=m) (ans+=i*(n+1)-2*s[i]+1)%=mod;
	}
	pr2(ans);
	return 0;
}

$E$

设第$i$个数最终去到$p_i$.

$\because |i-p_i|=\max (i-p_i,p_i-i)$.

$\therefore if|i-p_i|=i-p_i意味着向左走更优,可以发现a_i更大,p_i应该更小$

由此贪心思路可以得到一个区间DP的方法

#include
#include
#include
#define mk make_pair
using namespace std;
typedef long long ll;
const int N=2010;

int n;
pair<ll,ll> a[N];
ll f[N][N];
//f[i][j]表示前j-i+1个数选[i,j] 

int main() {
	scanf("%d",&n);
	for(int i=1;i<=n;i++) {
		ll x; scanf("%lld",&x);
		a[i]=mk(x,i);
	}
	sort(a+1,a+n+1);
	for(int i=1;i<=n;i++) f[i][i]=a[1].first*abs(a[1].second-i);
	for(int k=2;k<=n;k++) {
		int x=a[k].first,y=a[k].second;
		for(int i=1,j=k;j<=n;i++,j++) 
			f[i][j]=max(f[i][j-1]+x*llabs(y-j),f[i+1][j]+x*llabs(y-i));
	}
	printf("%lld\n",f[1][n]); return 0;
}
	

$F$

又是树形DP.

对于一个没有颜色$c$的大小为n的连通块,显然有$n\ast (n+1)/2$种路径不含颜色$c$.

由此发现求不含颜色$c$的路径数更方便.

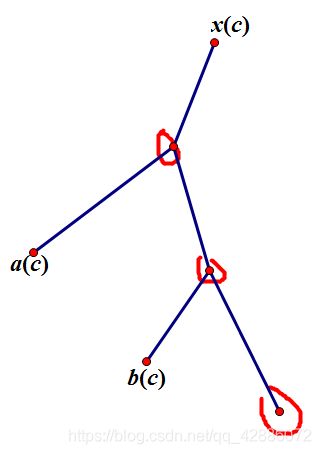
对于一个颜色为$c$的$x$节点,此时求一下对不含颜色$c$的路径数的贡献.

此时被圈出的点构成一个不含$c$的最大连通块.贡献为$3\ast 4/2=6$

DP过程维护不被圈出的点的数量即可.

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define lc (x<<1)
#define rc (x<<1|1)
#define gc getchar()//(p1==p2&&(p2=(p1=buf)+fread(buf,1,size,stdin),p1==p2)?EOF:*p1++)
#define mk make_pair
#define pi pair
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int N=2e5+10,size=1<<20;

//char buf[size],*p1=buf,*p2=buf;
template<class o> void qr(o &x) {
	char c=gc; x=0; int f=1;
	while(!isdigit(c)){if(c=='-')f=-1; c=gc;}
	while(isdigit(c)) x=x*10+c-'0',c=gc;
	x*=f;
}
template<class o> void qw(o x) {
	if(x/10) qw(x/10);
	putchar(x%10+'0');
}
template<class o> void pr1(o x) {
	if(x<0)x=-x,putchar('-');
	qw(x); putchar(' ');
}
template<class o> void pr2(o x) {
	if(x<0)x=-x,putchar('-');
	qw(x); puts("");
}

int n,a[N],sz[N],cnt[N];
ll ans[N];
vector<int>e[N];
void add(int x,int y) {e[x].push_back(y);}

ll f(ll n) {return n*(n+1)/2;}

void dfs(int x,int F) {
	int c=a[x];
	ll tot=cnt[c],last;
	sz[x]=1;
	for(auto y:e[x]) if(y^F) {
		last=cnt[c];
		dfs(y,x);
		ans[c]+=f(sz[y]-(cnt[c]-last));
		sz[x]+=sz[y];
	}
	cnt[c]=tot+sz[x];
}

int main() {
	qr(n);
	for(int i=1;i<=n;i++) qr(a[i]);
	for(int i=1,x,y;i<n;i++) 
		qr(x),qr(y),add(x,y),add(y,x);
	dfs(1,0); ll t=f(n);
	for(int i=1;i<=n;i++) pr2(t-(ans[i]+f(n-cnt[i])));
	return 0;
}

int main() {
qr(n);
for(int i=1;i<=n;i++) qr(a[i]);
for(int i=1,x,y;i qr(x),qr(y),add(x,y),add(y,x);
dfs(1,0); ll t=f(n);
for(int i=1;i<=n;i++) pr2(t-(ans[i]+f(n-cnt[i])));
return 0;
}