NC13950 Alliances(DFS序 + LCA)
题目链接
题意:
一 个 国 家 有 n 个 城 市 , 形 成 一 棵 树 , 有 n − 1 条 边 一个国家有n个城市,形成一棵树,有n-1条边 一个国家有n个城市,形成一棵树,有n−1条边
国 家 中 有 k 个 帮 派 , 分 别 占 领 一 些 城 市 国家中有k个帮派,分别占领一些城市 国家中有k个帮派,分别占领一些城市
每 个 帮 派 占 领 c i 个 城 市 , 以 及 这 c i 个 城 市 路 径 上 的 所 有 点 每个帮派占领c_i个城市,以及这c_i个城市路径上的所有点 每个帮派占领ci个城市,以及这ci个城市路径上的所有点
帮 派 可 以 联 盟 , 联 盟 会 将 几 个 帮 派 的 所 有 占 领 城 市 和 路 径 上 的 城 市 占 领 帮派可以联盟,联盟会将几个帮派的所有占领城市和路径上的城市占领 帮派可以联盟,联盟会将几个帮派的所有占领城市和路径上的城市占领
q 次 询 问 , 首 都 如 果 建 在 v 城 市 q次询问,首都如果建在v城市 q次询问,首都如果建在v城市
求 首 都 离 给 定 t i 个 帮 派 联 盟 中 最 近 占 领 城 市 的 距 离 求首都离给定t_i个帮派联盟中最近占领城市的距离 求首都离给定ti个帮派联盟中最近占领城市的距离
题解:
由 于 这 是 一 棵 树 , 路 径 只 有 一 条 , 那 么 就 假 设 根 为 1 由于这是一棵树,路径只有一条,那么就假设根为1 由于这是一棵树,路径只有一条,那么就假设根为1
那 么 就 可 以 用 L C A 找 到 这 些 帮 派 占 领 的 最 高 的 父 亲 节 点 那么就可以用LCA找到这些帮派占领的最高的父亲节点 那么就可以用LCA找到这些帮派占领的最高的父亲节点
求 出 每 个 帮 派 的 L C A 后 , 联 盟 的 时 候 , 找 这 几 个 帮 派 的 L C A 求出每个帮派的LCA后,联盟的时候,找这几个帮派的LCA 求出每个帮派的LCA后,联盟的时候,找这几个帮派的LCA
如 果 发 现 首 都 不 在 这 个 L C A 的 子 树 中 , 那 肯 定 最 短 距 离 就 是 到 这 个 L C A 的 距 离 如果发现首都不在这个LCA的子树中,那肯定最短距离就是到这个LCA的距离 如果发现首都不在这个LCA的子树中,那肯定最短距离就是到这个LCA的距离
树 上 两 点 距 离 可 以 用 两 点 的 深 度 和 减 去 2 倍 两 点 L C A 的 深 度 求 解 树上两点距离可以用两点的深度和减去2倍两点LCA的深度求解 树上两点距离可以用两点的深度和减去2倍两点LCA的深度求解
然 后 就 要 考 虑 如 果 首 都 建 在 这 个 子 树 里 然后就要考虑如果首都建在这个子树里 然后就要考虑如果首都建在这个子树里
子 树 里 可 能 刚 好 在 联 盟 占 领 的 城 市 里 , 或 者 不 在 子树里可能刚好在联盟占领的城市里,或者不在 子树里可能刚好在联盟占领的城市里,或者不在
由 于 每 次 询 问 给 出 的 联 盟 帮 派 个 数 不 是 很 多 由于每次询问给出的联盟帮派个数不是很多 由于每次询问给出的联盟帮派个数不是很多
所 以 直 接 暴 力 枚 举 这 些 联 盟 帮 派 , 找 最 近 点 所以直接暴力枚举这些联盟帮派,找最近点 所以直接暴力枚举这些联盟帮派,找最近点
这 时 候 就 要 用 到 d f s 序 这时候就要用到dfs序 这时候就要用到dfs序
利 用 二 分 在 每 个 帮 派 占 领 的 城 市 中 , 找 到 距 离 首 都 城 市 最 近 的 两 个 城 市 利用二分在每个帮派占领的城市中,找到距离首都城市最近的两个城市 利用二分在每个帮派占领的城市中,找到距离首都城市最近的两个城市
也 就 是 第 一 个 大 于 等 于 他 , 和 第 一 个 小 于 他 的 城 市 也就是第一个大于等于他,和第一个小于他的城市 也就是第一个大于等于他,和第一个小于他的城市
( 因 为 找 的 是 大 于 等 于 , 如 果 有 等 于 的 情 况 就 说 明 首 都 就 是 被 占 领 点 , 结 果 是 0 ) (因为找的是大于等于,如果有等于的情况就说明首都就是被占领点,结果是0) (因为找的是大于等于,如果有等于的情况就说明首都就是被占领点,结果是0)
由 于 首 都 是 在 联 盟 的 L C A 的 子 树 中 , 所 以 找 到 的 这 两 个 被 占 领 的 城 市 由于首都是在联盟的LCA的子树中,所以找到的这两个被占领的城市 由于首都是在联盟的LCA的子树中,所以找到的这两个被占领的城市
到 他 们 父 亲 结 点 的 路 径 一 定 全 部 都 是 被 占 领 的 到他们父亲结点的路径一定全部都是被占领的 到他们父亲结点的路径一定全部都是被占领的
所 以 想 要 找 最 近 的 , 就 应 该 找 到 首 都 和 他 们 的 L C A 所以想要找最近的,就应该找到首都和他们的LCA 所以想要找最近的,就应该找到首都和他们的LCA
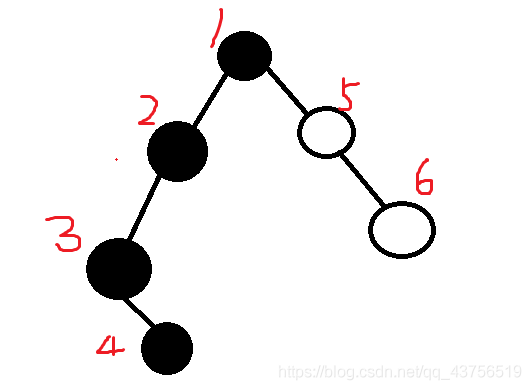
这 个 图 中 , 假 设 黑 色 是 被 占 领 点 , 如 果 1 和 4 被 占 领 这个图中,假设黑色是被占领点,如果1和4被占领 这个图中,假设黑色是被占领点,如果1和4被占领
1 就 是 这 个 联 盟 占 领 的 最 高 点 , 将 在 6 建 首 都 , 6 在 最 高 点 的 子 树 中 1就是这个联盟占领的最高点,将在6建首都,6在最高点的子树中 1就是这个联盟占领的最高点,将在6建首都,6在最高点的子树中
标 注 的 123456 代 表 的 就 是 d f s 序 , 6 相 邻 最 近 被 占 领 的 点 是 4 标注的123456代表的就是dfs序,6相邻最近被占领的点是4 标注的123456代表的就是dfs序,6相邻最近被占领的点是4
但 是 4 到 6 的 距 离 明 显 没 有 1 到 6 近 , 所 以 要 进 行 对 4 和 6 求 L C A 但是4到6的距离明显没有1到6近,所以要进行对4和6求LCA 但是4到6的距离明显没有1到6近,所以要进行对4和6求LCA
然 后 再 计 算 这 个 L C A 到 6 的 距 离 才 是 最 近 的 然后再计算这个LCA到6的距离才是最近的 然后再计算这个LCA到6的距离才是最近的
找 第 一 个 大 于 等 于 首 都 d f s 序 的 点 也 是 类 似 道 理 找第一个大于等于首都dfs序的点也是类似道理 找第一个大于等于首都dfs序的点也是类似道理
这 个 图 没 有 表 示 全 部 情 况 , 只 举 例 说 了 一 下 找 第 一 个 小 于 的 这个图没有表示全部情况,只举例说了一下找第一个小于的 这个图没有表示全部情况,只举例说了一下找第一个小于的
然 后 在 这 两 个 点 都 能 取 到 的 情 况 下 取 最 小 结 果 , 就 是 最 终 答 案 然后在这两个点都能取到的情况下取最小结果,就是最终答案 然后在这两个点都能取到的情况下取最小结果,就是最终答案
AC代码
/*
Author : zzugzx
Lang : C++
Blog : blog.csdn.net/qq_43756519
*/
#include