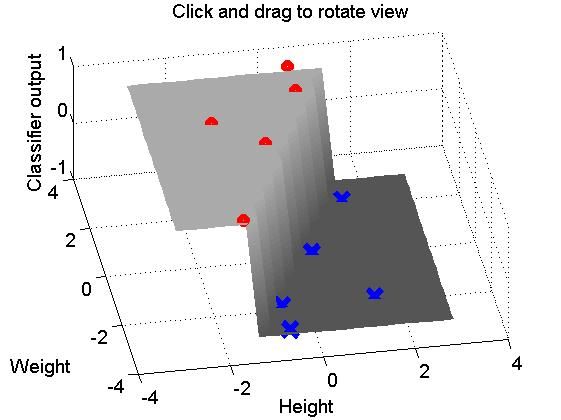
%%%% Tutorial on the basic structure of using a planar decision boundary %%%% to divide a collection of data-points into two classes. %%%% by Rajeev Raizada, Jan.2010 %%%% %%%% Please mail any comments or suggestions to: raizada at cornell dot edu %%%% %%%% Probably the best way to look at this program is to read through it %%%% line by line, and paste each line into the Matlab command window %%%% in turn. That way, you can see what effect each individual command has. %%%% %%%% Alternatively, you can run the program directly by typing %%%% %%%% classification_plane_tutorial %%%% %%%% into your Matlab command window. %%%% Do not type ".m" at the end %%%% If you run the program all at once, all the Figure windows %%%% will get made at once and will be sitting on top of each other. %%%% You can move them around to see the ones that are hidden beneath. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%% Let's look at a toy example: classifying people as either %%%% sumo wrestlers or basketball players, depending on their height and weight. %%%% Let's call the x-axis height and the y-axis weight sumo_wrestlers = [ 4 8; ... 2 6; ... 2 2; ... 3 5; ... 4 7]; basketball_players = [ 3 2; ... 4 5; ... 5 3; ... 5 7; ... 3 3]; %%% Let's plot this figure(1); clf; set(gca,'FontSize',14); plot(sumo_wrestlers(:,1),sumo_wrestlers(:,2),'ro','LineWidth',2); hold on; plot(basketball_players(:,1),basketball_players(:,2),'bx','LineWidth',2); axis([0 6 0 10]); xlabel('Height'); ylabel('Weight'); legend('Sumo wrestlers','Basketball players',2); % The 2 at the end means % put the legend in top-left corner %%%% In order to be able to train a classifier on the input vectors, %%%% we need to know what the desired output categories are for each one. %%%% Let's set this to be +1 for sumo wrestlers, and -1 for basketball players desired_output_sumo = [ 1; ... % sumo_wrestlers = [ 4 8; ... 1; ... % 2 6; ... 1; ... % 2 2; ... 1; ... % 3 5; ... 1 ]; % 4 7]; desired_output_basketball = [ -1; ... % basketball_players = [ 3 2; ... -1; ... % 4 5; ... -1; ... % 5 3; ... -1; ... % 5 7; ... -1 ]; % 3 3 ]; all_desired_output = [ desired_output_sumo; ... desired_output_basketball ]; %%%%%% We want to find a linear decision boundary, %%%%%% i.e. simply a straight line, such that all the data points %%%%%% on one side of the line get classified as sumo wrestlers, %%%%%% i.e. get mapped onto the desired output of +1, %%%%%% and all the data points on the other side get classified %%%%%% as basketball players, i.e. get mapped onto the desired output of -1. %%%%%% %%%%%% The equation for a straight line has this form: %%%%%% weight_vector * data_coords - offset_from_origin = 0; %%%%%% %%%%%% We're not so interested for now in the offset_from_origin term, %%%%%% so we can get rid of that by subtracting the mean from our data, %%%%%% so that it is all centered around the origin. %%%%%% Let's stack up the sumo data on top of the bastetball players data all_data = [ sumo_wrestlers; ... basketball_players ]; %%%%%% Now let's subtract the mean from the data, %%%%%% so that it is all centered around the origin. %%%%%% Each dimension (height and weight) has its own column. mean_column_vals = mean(all_data); %%%%%% To subtract the mean from each column in Matlab, %%%%%% we need to make a matrix full of column-mean values %%%%%% that is the same size as the whole data matrix. matrix_of_mean_vals = ones(size(all_data,1),1) * mean_column_vals; zero_meaned_data = all_data - matrix_of_mean_vals; %%%% Now, having gotten rid of that annoying offset_from_origin term, %%%% we want to find a weight vector which gives us the best solution %%%% that we can find to this equation: %%%% zero_meaned_data * weights = all_desired_output; %%%% But, there is no such perfect set of weights. %%%% We can only get a best fit, such that %%%% zero_meaned_data * weights = all_desired_output + error %%%% where the error term is as small as possible. %%%% %%%% Note that our equation %%%% zero_meaned_data * weights = all_desired_output %%%% %%%% has exactly the same form as the equation %%%% from the tutorial code in %%%% http://www.dartmouth.edu/~raj/Matlab/fMRI/design_matrix_tutorial.m %%%% which is: %%%% Design matrix * sensitivity vector = Voxel response %%%% %%%% The way we solve the equation is exactly the same, too. %%%% If we could find a matrix-inverse of the data matrix, %%%% then we could pre-multiply both sides by that inverse, %%%% and that would give us the weights: %%%% %%%% inv(zero_meaned_data) * zero_meaned_data * weights = inv(zero_meaned_data) * all_desired_output %%%% The inv(zero_meaned_data) and zero_meaned_data terms on the left %%%% would cancel each other out, and we would be left with: %%%% weights = inv(zero_meaned_data) * all_desired_output %%%% %%%% However, unfortunately there will in general not exist any %%%% matrix-inverse of the data matrix zero_meaned_data. %%%% Only square matrices have inverses, and not even all of them do. %%%% Luckily, however, we can use something that plays a similar role, %%%% called a pseudo-inverse. In Matlab, this is given by the command pinv. %%%% The pseudo-inverse won't give us a perfect solution to the equation %%%% zero_meaned_data * weights = all_desired_output %%%% but it will give us the best approximate solution, which is what we want. %%%% %%%% So, instead of %%%% weights = inv(zero_meaned_data) * all_desired_output %%%% we have this equation: weights = pinv(zero_meaned_data) * all_desired_output; %%%% Let's have a look at how these weights carve up the input space %%%% A useful Matlab command for making grids of points %%%% which span a particular 2D space is called "meshgrid" [input_space_X, input_space_Y] = meshgrid([-3:0.3:3],[-3:0.3:3]); weighted_output_Z = input_space_X*weights(1) + input_space_Y*weights(2); %%%% The weighted output gets turned into the category-decision +1 %%%% if it is greater than 0, and -1 if it is less than zero. %%%% The easiest way to map positive numbers to +1 %%%% and negative numbers to -1 %%%% is by first mapping them to 1 and 0 %%%% by the inequality-test(weighted_output_Z>0) %%%% and then turning 1 and 0 into +1 and -1 %%%% by multipling by 2 and subtracting 1. decision_output_Z = 2*(weighted_output_Z>0) - 1; figure(2); clf; hold on; surf(input_space_X,input_space_Y,decision_output_Z); %%% Let's show this decision surface in gray, from a good angle colormap gray; caxis([-3 3]); %%% Sets white and black values to +/-3, so +/-1 are gray shading interp; %%% Makes the shading look prettier grid on; view(-10,60); rotate3d on; %%% Make it so we can use mouse to rotate the 3d figure set(gca,'FontSize',14); title('Click and drag to rotate view'); %%%% Let's plot the zero-meaned sumo and basketball data on top of this %%%% Each class has 5 members, in this case, so we'll subtract %%%% a mean-column-values matrix with 5 rows, to make the matrix sizes match. one_class_matrix_of_mean_vals = ones(5,1) * mean_column_vals; zero_meaned_sumo_wrestlers = sumo_wrestlers - one_class_matrix_of_mean_vals; zero_meaned_basketball_players = basketball_players - one_class_matrix_of_mean_vals; plot3(zero_meaned_sumo_wrestlers(:,1),zero_meaned_sumo_wrestlers(:,2), ... desired_output_sumo,'ro','LineWidth',5); hold on; plot3(zero_meaned_basketball_players(:,1),zero_meaned_basketball_players(:,2), ... desired_output_basketball,'bx','LineWidth',5,'MarkerSize',15); xlabel('Height'); ylabel('Weight'); zlabel('Classifier output');
分类前:
分类后: