动态规划----走迷宫
忙碌了一段时间,博客也停下来了。因为之前学习的方向一直是学技术栈道,确忽略了算法的学习。最近也就一直在刷算法题目。之前尝试过很多次,但是每次总是感觉自己脑子不够用,觉得自己笨笨的。这次下定决心,想着多刷题,总能够明白一点的 初衷。又开始被算法蹂躏的旅行…
动态规划
这个名字特别的高级,因为每次碰到动态规划的时候,都会害怕,对它也有恐惧感觉,说白了,那就是每次都不会做。好了开始正文吧。
那么到底什么是动态规划呢!网上大多数的解释那就是 用专业的词语,在解释专业的话。到来还是不太理解。
我个人的理解就是动态的推导。动态规划可以从下面几个要素来解题:
1.先递归找出解题方法
2.记忆化优化递归
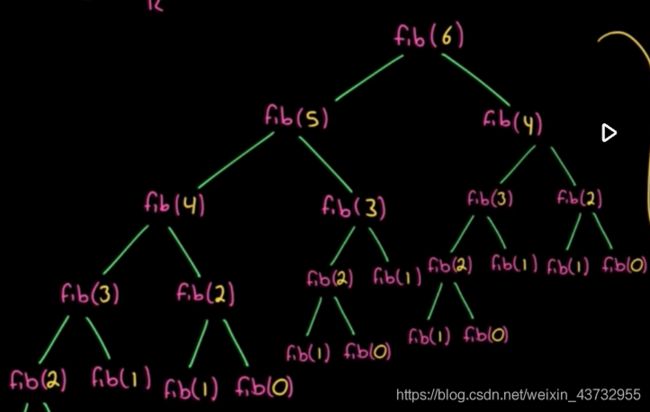
这个递归有个很严重的问题,就是有大量的重复子问题,计算f(2)的时候 会计算f(0),f(1).。计算f(3)的时候也会计算。那么我们就可尝试用一个记忆容器,把我们之前计算出的结果存储起来。然后每次获取结果的时候先从记忆容器中获取,有则取出来 无则放进去。
3.尝试自底向上解题
这个的第一件事就是找出关系方程
F(n) = F(n-1)+F(n-2)。这个是斐波拉契的关系方程。那么是否可以从底端开始 计算呢。
f(0) = 0 f(1)=1
for 2==>n
f(n) = f(n-1)+f(n-2)
下面看这个迷宫的问题:

题目描述如下:小人从左上方的位置出发,他只能向下或者向右走,每次只能走一步,并且红色的方格是障碍物,不能通过。求从start位置到 end位置有多少种走法?
1.递归解题

如上图:start位置上的走法 = A位置上的走法+B位置上的法;B位置上的走法 = C位置上的走法 + E位置上的走法
可以这样一直递归下去。解题。但是如同斐波拉契中的递归有着相同的问题 那就是有大量重复的子问题 。如在求A位置上的走法时要求C和D位置上的走法。但是在求B时 已经求过C了。
解决方法: 同样也是使用记忆的方法。
3.尝试自底向上解题
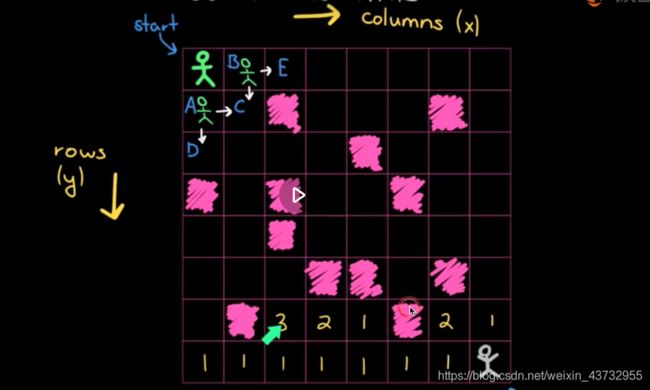
从end上开始 数字代表在该空格上 有的走法。如上图所示 我们能很轻易的推导出 那么之间的关系式:
动态转移方程:opt[i,j] = opt[i][j+1]+opt[i+1][j] 当碰到障碍物时那也就是0。
按照这个推导关系能获得整个图的走法分布图:

那么我们只要自底向上 就可以推导出 最上面start位置上的走法了.具体代码如下:
package leetcode;
import org.junit.Test;
/**
* @author liuzihao
* @create 2019/12/8-10:14
* 动态规划,走迷宫
*/
public class DemoDY1 {
@Test
public void test() {
// 初始化迷宫 1代表有石头的障碍,从最左上角开始走 然后走到最右下方
int[][] arr = {
//start
{0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 1, 0, 0, 0, 1, 0},
{0, 0, 0, 0, 1, 0, 0, 0},
{1, 0, 1, 0, 0, 1, 0, 0},
{0, 0, 1, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 1, 0, 1, 0},
{0, 1, 0, 0, 0, 1, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0} //end
};
int[][] opt = new int[arr.length][arr.length];
/**
* opt:此节点的最多走法 = 此节点左、下 opt之和
* opt[i,j] = opt[i,j+1]+opt[i+1,j] 碰到石头(1)。opt[i,j]=0
*/
for (int i = arr.length - 1; i >= 0; i--) {
for (int j = arr[0].length - 1; j >= 0; j--) {
//如果碰到的是 石头障碍 (数组中的1代表障碍物)
if (arr[i][j] == 1) {
opt[i][j] = 0;
continue;
}
//初始化 紧邻end的两个方块的opt。他们的可行方案分别只有一种
if ((i == arr.length - 1 && j == arr.length - 2) || (i == arr.length - 2 && j == arr.length - 1)) {
opt[i][j] = 1;
continue;
}
opt[i][j] = _gen(opt, i, j);
}
}
System.out.println(opt[0][0]);
//打印迷宫的步数表格
}
//根据动态转移方程 自底向下获得opt
int _gen(int[][] opt, int i, int j) {
//如果是边缘 设置为0
return _get(opt, i, j + 1) + _get(opt, i + 1, j);
}
//初始化 最左一列 和最下一行的数据时要特殊处理 。因为此时数组会越界
int _get(int[][] opt, int i, int j) {
if (i >= opt.length || j >= opt.length) return 0;
return opt[i][j];
}
}
截图来自:极客时间 面试算法通关