数据结构：平衡二叉树（AVL树），伸展树，B-树

AVL树（平衡二叉查找树）

同样的数据，不同的插入顺序，将导致不同的深度和平均查找长度ASL（刻画查找效率）。

为了加速搜索，可以使用二叉树，但是二叉树不加限制的话，可能会出现“八”字型的情况，导致O(N).

定义：

一棵AVL树是其每个节点的左子树和右子树的高度最多差1的二叉查找树。

即带有平衡条件的二叉查找树。

平衡因子：子树高度差。Balance Factor（简称BF）。BF( T ) = hL - hr

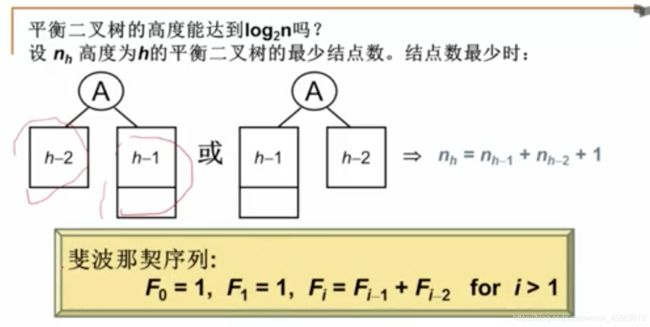
给定节点数为n的AVL树的最大高度为O(${\log }_{2}n$)。空树的高度定义为-1.

插入数据时可能破坏AVL树的特性，需要对树进行简单的修正，称之为**“旋转”**

旋转

插入一个新的点以后，只有从插入点到根结点路径上的节点的平衡可能会被打破，因为只有这些节点的子树可能变化。沿着这条路径上行到根并更新平衡信息，在找到的第一个破坏了平衡的节点，重新平衡这棵树。下面的讨论都是在这个“根节点”进行调整的。

单旋转

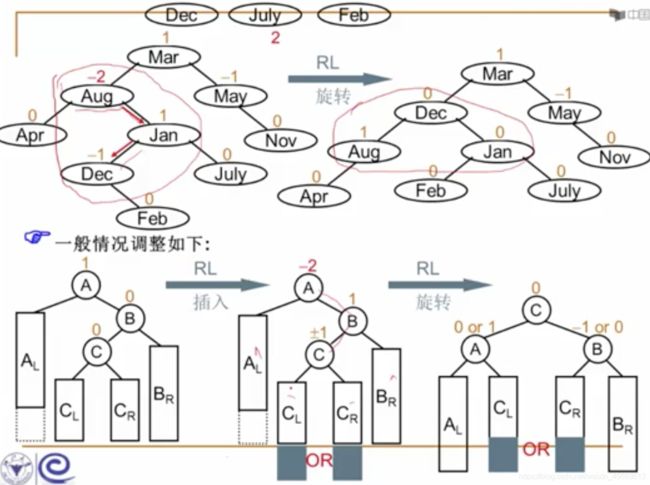
单旋转，适用于对该节点的左子树的左子树进行插入，或者对右子树的右子树进行插入。（LL-Rotation / RR-Rotation)这里不在乎最后插到的位置是左还是右，只要是在**“发现者”的右子树的右子树，或“发现者”**的左子树的左子树进行插入，就适用。

B节点，是发现者节点的右子节点，把它提上来，把BL挂到A的右子树的位置，因为BL按照查找树的定义，是小于B而大于A的。这里可以看成是一个摩天轮旋转，掉一个物块到旁边的房间。

（上图为在右子树的右子树进行插入的示意图，注意，该图体现出了在最后插入的是左还是右无所谓，重点是插入在了右子树的右子树，这个时候只需要把被破坏者的右子树提上去，把提上来的这个节点的左子树挂靠过去就行了）

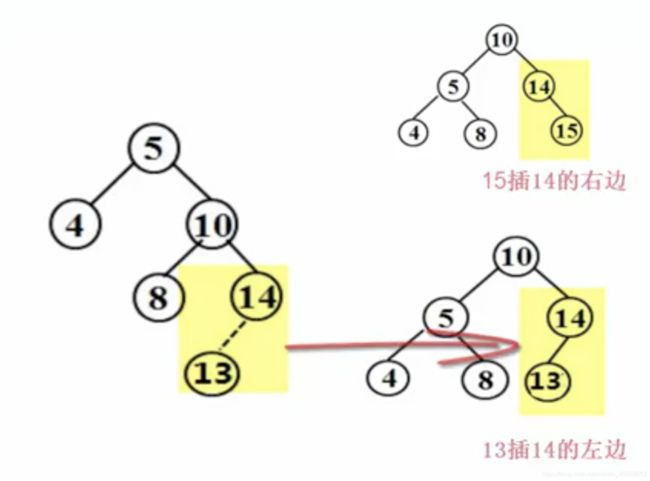
重点：找到被破坏者（finder）和破坏者（trouble maker）及其之间的关系！

LL旋转同理，即插入在左子树的左子树的情况。

上图还体现了一个点：最开始的时候May和Mar都不平衡，在对Mar重新调整平衡以后，May自己就平衡了。所以只需要上行找到第一个不平衡的点调整即可。

双旋转

双旋转，适用于对该节点的**左儿子的右子树或右儿子的左子树**进行插入。（LR-Rotation / RL-Rotation）

上图为插入点（麻烦节点）在发现者的左子树的右子树中，为LR插入。

核心：重构A、B、C三个点！把中间大小的当作新的根，小的放左边大的放右边，目的是仍保持查找树的性质！然后延伸下来可以有四个子树，分别对应回去就好了。

RL插入，同理，核心还是调整ABC这三个节点。

平衡二叉树调整的模式，任何情况下都归结为以上四种模式：LL旋转、RR旋转、LR旋转、RL旋转。核心是判断关系：插入节点把谁的平衡破坏了，他与被破坏者是什么关系。在调整的过程中时刻保持查找树的性质：左边都比他小，右边都比他大。

注意：有时候插入元素即便不需要调整结构，也可能需要重新计算一些平衡因子！

关于平衡因子的计算：【书P93】

定义AVL树节点的结构体的时候，就包含一个 int Height;

Height(Position P)
{
  if(p==NULL)
    return -1;
  else
    return P->Height;
}

后面引用的时候，可以直接：

...
if( Height(T->Right) - Height(T->Left) == 2)	//肯定后面还要有Left-Right==2的
{
  ...
}

***注意：把节点拎上去的时候，断的是哪条边！

方法：2边的“摆”压进来，把原来的“摆”挤压到下面去了。

伸展树

基本想法：当一个节点被访问后，它就要经过一系列AVL树的旋转后放到根上。

实际效用：当一个节点被访问时，它就很可能不久再被访问到。

书P97 “展开”

目的：把要访问的目标节点X调整为根节点

核心是分三种类型讨论：

1、访问节点X的父结点为整棵树的根节点：只需要旋转X和树根即可，且这是沿着访问路径上的最后的旋转。

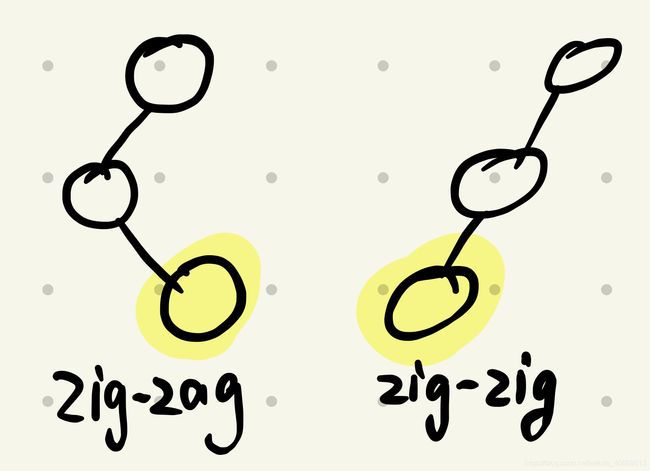
2、访问节点X有父结点，也有祖父结点，且构成之字形（zig-zag)：执行一次像AVL一样的双旋转。

3、访问节点X有父结点，也有祖父结点，且为直线形（zig-zig)：

​ 以下图为例，是左直线：从根结点的左子节点开始，把每个节点依次拎上去（也是旋转），一直到把这个节 点拎成根结点为止。

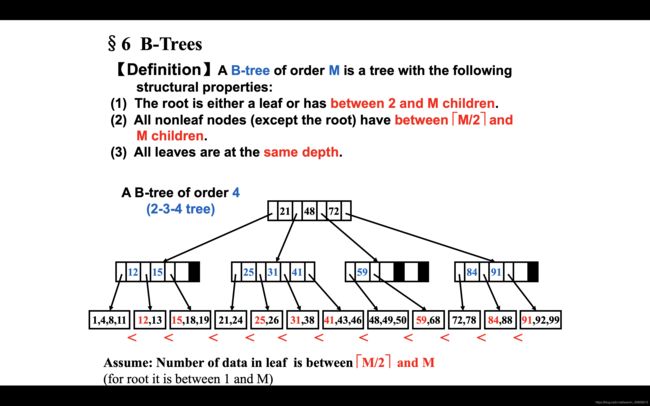
B-树

一个M阶B-树的性质：

• 根结点是个叶子结点，或者有2到M个子节点。
• 非叶子结点（除了根以外），有「M/2】到M个节点。（M/2向上取整）
• 所有的叶子结点同深度。
  

例题：