图论算法的基础知识

图的表示
如果有向图是稠密的，也就是图中的边数 |E| 和定点数 |V| 满足如下关系 |E|=O(|V|2) 。那么我们就用二维数组来表示，如果有向图是稀疏的，也就是边数相当的少，那么我们就用邻接表来表示。它就是一个结构体数组，每个元素表示一个顶点，然后指向它的所有相邻的顶点（这个相邻是指出边）。
实际情况下，顶点名称都是字符串，我们需要把字符串映射成数字，这样容易处理，通常的做法就是用一个散列表来记录这种映射，关键字是这个字符串，值为赋给的数字。
但是在进行输出时，我们还是需要将数字变成相应的字符串，这样我们可以事先做一个字符串数组，这样就可以完成映射。

---

图论中常见的问题
1.拓扑排序.
算法1.1. 这个是针对有向无圈图来说的，如果顶点 v 有指向 w 的边，那么我们就将 v 排在 w 前面。如果图中有圈，这就不可能进行拓扑排序。首先，我们用时间复杂度为 O(|V|2) 的算法来实现。
我们所用的图如下图所示

#include 
#include 
struct node
{
    int num;
    struct node *next;
};
typedef struct node * Node;
struct graph
{
    int node_num;
    Node *table;
};
typedef struct graph * Graph;
int Find_next_zero_degree(int *a,int n)
{
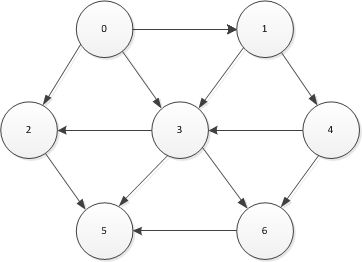
    int i;
    for(i=0;iif(a[i]==0)
        {
            a[i]=-1;
            return i;
        }

    }
    return -1;
}
int* Topsort(Graph g,int in[])
{
    n=g->node_num;
    int i,temp_int;
    int *Topnum=malloc(sizeof(int)*n);
    Node temp;
    for(i=0;iif(temp_int==-1)
        {
            printf("error,graph has a cycle");
            break;
        }
        Topnum[temp_int]=i+1;
        temp=g->table[temp_int]->next;
        while(temp!=NULL)
        {
            in[temp->num]--;
            temp=temp->next;
        }
    }
    return Topnum;
}
int main()
{
//因为没有办法直接读图，所以将图的信息转化成如下的矩阵信息，然后由这个矩阵来生成相应的邻接表，再对邻接表进行处理
    int Array[7][7]={{0,1,1,1,0,0,0},{0,0,0,1,1,0,0},{0,0,0,0,0,1,0},{0,0,1,0,0,1,1},{0,0,0,1,0,0,1},{0,0,0,0,0,0,0},{0,0,0,0,0,1,0}};
    Graph Adj_list=malloc(sizeof(struct graph));
    Adj_list->node_num=7;
    Adj_list->table=malloc(sizeof(struct node *)*7);
    Node temp;
    int i,j;
    int Indegree[7]={0,1,2,3,1,3,2};
    //将图读入邻接表中
    for(i=0;i<7;i++)
    {
        Adj_list->table[i]=malloc(sizeof(struct node));
        Adj_list->table[i]->num=i;
        Adj_list->table[i]->next=NULL;
        temp=Adj_list->table[i];
        for(j=0;j<7;j++)
        {
            if(Array[i][j]==1)
            {
                Node new_node=malloc(sizeof(struct node));
                new_node->num=j;
                new_node->next=NULL;
                temp->next=new_node;
                temp=temp->next;
            }
        }
    }

    int *Topnum=Topsort(Adj_list,Indegree,7);
    for(i=0;i<7;i++)
    {
        printf("%d ",Topnum[i]);
    }
}

这种算法的思想就是，首先将每个顶点的入度列到一个数组中记为Indegree，首先找到顶点集中入度为0的顶点，如果没有入度为零的顶点，那么说明这个图是有圈的，是不存在拓扑排序的。然后将顶点为入度为零的点相邻的点的入度减1，输出这个顶点。再从Indegree中寻找下一个顶点入度为零的点，依次这样进行，直到所有的点全部输出为止。

算法1.2. 上述算法的时间复杂度比较大，所以下面对算法1的时间复杂度进行改进。我们首先将入度为零的顶点筛选出来，放入到队列中，这个时间复杂度为 O(n) ，然后令一个顶点A出列，让这个顶点的相邻点的入度减1,时间复杂度为 O(k) ，k表示A的邻点的个数。然后看这些邻点的入度是否为零，如果为零，那么让这些邻点入队列，如果都不为零，说明这个图中有圈的存在，不存在拓扑排序。总的来说，时间复杂度为 O(n+m) ，m为边的个数。算法的实现如下：

int* algorithm2(Graph g,int *Ind)
{
    int n=g->node_num;
    int queue[n+1];
    int head=0,rear=0;
    int zero_ele;
    int i;
    int order=0;
    Node temp;
    int *result=malloc(sizeof(int)*n);
    //对Ind进行扫描，选出所有入度为零的点
    for(i=0;iif(Ind[i]==0)
        {
            queue[rear]=i;
            rear++;
        }
    }
    if(rear==0)
    {
        printf("error,the graph has a cycle\n");
        return NULL;
    }
    while(head!=rear)
    {
        zero_ele=queue[head];
        result[zero_ele]=++order;
        head++;
        temp=g->table[zero_ele]->next;
        while(temp!=NULL)
        {
            Ind[temp->num]--;
            if(Ind[temp->num]==0)
            {
                queue[rear]=temp->num;
                rear++;
            }
            temp=temp->next;
        }
    }
    free(queue);
    if(head!=n)
    {
        printf("error,the graph has a cycle\n");
        return NULL;
    }
    else
        return result;
}

---

2.最短路径算法. 我们主要考虑单源最短路径问题，也就是给定一个赋权图G=(V,E)，和一个特定的顶点s作为输入，找出从s到G中每一个其他顶点的最短赋权路径。
2.1无权图最短路径
无权就表示图中的边的权重为1.首先我们用一个时间复杂度为 O(|V|2) 的算法来解决无权有向图中的单源最短路径问题。
算法2.1.1 首先，从一个特定的顶点s出发，那么从s到s的最短路径长度就是0；然后，我们找到和s相邻的顶点，这些顶点到s的最短距离就是1，我们将这些顶点进行标记，表示已经找到s到这些顶点的最短路径。接下来，我们要找到距离s为2的顶点，我们可以从s的邻点a出发，找到距离a为1的那些没有被标记的顶点，显然s到这些顶点的最短路径为2.随后对这些顶点进行标记。直到所有的点都被标记，程序就结束了。具体的代码实现如下

struct info
{
    int distance;//表示到特定的s点的最短路径长度
    int before;//表示这个点的上一个定点
    int sign;//是否已经被处理
};
typedef struct info *Info;
Info* shortest_path(int vertex,Graph g)
{
    int n=g->node_num;
    //构造信息表
    Info *information=malloc(sizeof(struct info*)*n);
    int i;
    for(i=0;istruct info));
        information[i]->distance=Max;
        information[i]->before=-1;
        information[i]->sign=0;
    }
    information[vertex]->distance=0;
    int  currdist=0;
    int sum_sign=0;
    Node temp;
    for(currdist=0;currdistif(sum_sign==n)
            break;
        for(i=0;iif(information[i]->distance==currdist&&information[i]->sign==0)
            {
                information[i]->sign=1;
                sum_sign++;
                temp=g->table[i]->next;
                while(temp!=NULL)
                {
                    if(information[temp->num]->before==-1)
                    {
                        information[temp->num]->distance=currdist+1;
                        information[temp->num]->before=i;
                    }
                    temp=temp->next;

                }
            }
        }
    }
    return information;
}

算法的主干由两个for循环构成，最坏情况下，currdist=d-1，这时候图就是一个链状结构,所以最坏情况下的时间复杂度为 O(n2) 。
算法2.1.2. 我们可以类似改进拓扑排序那样对算法1进行改进，首先让需要求它到其他各点最短路径的点入队列，它进行处理时，让它出队列，然后对它的邻点进行处理，更改邻点在信息表中的信息，然后让邻点入队列，知道队列为空结束。相应的代码如下

Info *algorithm2_short(int vertex,Graph g)
{
    int n=g->node_num;
    //构造信息表
    Info *information=malloc(sizeof(struct info*)*n);
    int queue[n];
    int head=0;
    int rear=0;
    int i;
    for(i=0;imalloc(sizeof(struct info));
        information[i]->distance=Max;
        information[i]->before=-1;
        information[i]->sign=0;
    }
    information[vertex]->distance=0;
    queue[rear]=vertex;
    rear++;
    int currverdex=0;
    Node temp;
    while(head!=rear)
    {
        currverdex=queue[head];
        head++;
        information[currverdex]->sign=1;
        temp=g->table[currverdex]->next;
        while(temp!=NULL)
        {
            if(information[temp->num]->before==-1)
            {
                information[temp->num]->distance=information[currverdex]->distance+1;
                information[temp->num]->before=currverdex;
                queue[rear]=temp->num;
                rear++;
            }
            temp=temp->next;
        }
    }
    return information;
}

进入队列时，我们先检验是否这个点已经进入队列，如果进入队列，就不在让其进入队列。这样最多是所有的点都进入了一次队列，然后在对每个出队列的节点的邻点进行信息更新，这所花费的时间就是它的出边数，所以这个时间复杂度为 O(|V|+|E|)
2.2非负有向加权图最短路径.
我们考虑如下的非负有向加权图

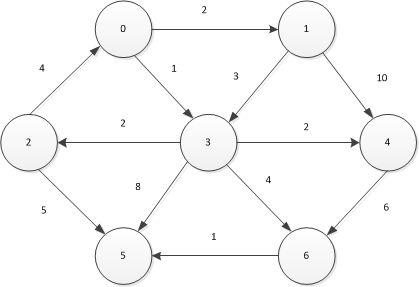
当图中没有负值权重时，我们可以证明运用Dijkstra算法可以解决最短路径问题。过程如下，首先选择一个点a，作为出发点，然后将它的邻点b的信息进行更新，更新的内容为到目前为止，从a到b的最短距离，所谓到目前为止就是从a出发，经过已经处理过的点到b。然后就是贪心算法，我们选择当前没有被处理过的点中距离a的最短的点，对这个点进行处理，把它更新为已处理点，把它的邻点进行更新，使得它的邻点到a的距离为到目前为止最短的。可以证明，c是将要被处理的点，那么我们就说从a到c的最短路径m已经确定，它是目前经过已处理的点到c的最短路径，也是全局的从a到c的最短路径，原因在如果存在另一个最短路径 l ，使得从a到c的距离比m短，那么 l 必须经过a的邻点，我们假设为d，同时 l 必然要经过一个未被处理的点f，然后才能到c，这显然已经违背了选择下一个要处理的点的原则–就是这个点是当前未被处理的点中与a距离最短的点。我们之所以选择c为下一个要处理的点的原因就是c与a的距离小于f和a的距离。



下面实现这个算法的代码：

#include 
#include 
#define MAX 10000
struct node
{
    int num;
    int weight;
    struct node *next;
};
typedef struct node * Node;
struct graph
{
    int node_num;
    Node *table;
};
typedef struct graph * Graph;
struct info
{
    int distance;//表示到特定的s点的最短路径长度
    int before;//表示这个点的上一个定点
    int sign;//是否已经被处理
};
typedef struct info *Info;
//Dijkstra
Info *Dijkstra(int vertex,Graph g)
{
    int vertex_n=g->node_num;
    Info * info_table=malloc(sizeof(Info)*vertex_n);
    int i;
    Node temp;
    for(i=0;istruct info));
        info_table[i]->distance=MAX;
        info_table[i]->before=-1;
        info_table[i]->sign=0;
    }
    info_table[vertex]->distance=0;
    for(;;)
    {
        int min_dist=MAX;
        int min_vertex;
        int new_len;
        for(i=0;iif(min_dist>info_table[i]->distance&&info_table[i]->sign==0)
            {
                min_dist=info_table[i]->distance;
                min_vertex=i;
            }
        if(min_dist==MAX)
            break;
        info_table[min_vertex]->sign=1;
        temp=g->table[min_vertex]->next;
        while(temp!=NULL)
        {
            new_len=info_table[min_vertex]->distance+temp->weight;
            if(new_lennum]->distance)
            {
                info_table[temp->num]->distance=new_len;
                info_table[temp->num]->before=min_vertex;
            }
            temp=temp->next;
        }
    }
    return info_table;
}

主函数为

int main()
{
    int Array[7][7]={{0,2,0,1,0,0,0},
                    {0,0,0,3,10,0,0},
                    {4,0,0,0,0,5,0},
                    {0,0,2,0,2,8,4},
                    {0,0,0,0,0,0,6},
                    {0,0,0,0,0,0,0},
                    {0,0,0,0,0,1,0}};
    Graph Adj_list=malloc(sizeof(struct graph));
    Adj_list->node_num=7;
    Adj_list->table=malloc(sizeof(struct node *)*7);
    Node temp;
    int i,j;
    //将图读入邻接表中
    for(i=0;i<7;i++)
    {
        Adj_list->table[i]=malloc(sizeof(struct node));
        Adj_list->table[i]->num=i;
        Adj_list->table[i]->weight=0;
        Adj_list->table[i]->next=NULL;
        temp=Adj_list->table[i];
        for(j=0;j<7;j++)
        {
            if(Array[i][j]!=0)
            {
                Node new_node=malloc(sizeof(struct node));
                new_node->num=j;
                new_node->weight=Array[i][j];
                new_node->next=NULL;
                temp->next=new_node;
                temp=temp->next;
            }
        }
    }
    Info *information=Dijkstra(0,Adj_list);
}

这个Dijkstra算法的时间复杂度为 O(|E|+|V|2) ,原因是算法的每一步都要计算出最小距离的点，这个时间消耗是 O(|V|) 。如果 |E|=O(|V|2) ,这种方法是比较好的，但是如果边是稀疏的那么这种方法就比较浪费时间。改进方法牵扯到配对堆和斐波那契堆的使用，这里暂且不讲。
同时由于这种算法是贪心算法，它每次都要选择最短的当前距离，所以是不能用队列实现像无权图那样的改进的。
2.3.无圈图. 假设一个赋权有向图是无圈的，那么我们就可以运用拓扑排序来实现寻找最短路径问题。我们的目的是要找出从 a 到其他各顶点的最短路径。首先，我们对这个图所有顶点进行拓扑排序，我们注意排在 a 之前的顶点是从 a 无法到达的，所以排在 a 之前的顶点的信息进行更新时，只需标记为已处理状态，从 a 可以到达的顶点一定是排在 a 之后的，但是 a 不一定能够到达所有排在它之后的顶点。在拓扑排序进行过程中，我们需要对 a 的邻点的入度进行减1处理，这个时候对 a 的邻点进行信息的更新，更新内容包括当前距离（distance），以及路径上一个节点（before）。针对进入队列中的点，如果它的距离仍然是无穷大，那么说明 a 无法到达这个顶点的，把它标记为已处理，对其邻点只进行入度减一操作，否者，对其邻点再增加信息更新操作，包括当前最短路径距离（distance）和路径的上一个节点（before），进入队列中的点，如果 a 可以到达它，那么它的最短路径是已经确定的，原因是没有未知（也就是没有进行拓扑排序的）的节点可以进入它，显然他的最短路径不可能再被更新。这样，我们只需对所有的点和所有的边进行一次的遍历，就可以完成最短路径的确定问题。代码如下：

Info * top_path(Graph g,int *Indegree,int vertex)
{
    int vertex_n=g->node_num;
    int queue[vertex];
    int head=0;
    int rear=0;
    int i;
    //信息表的确定
    Info *info_table=malloc(sizeof(Info)*vertex_n);
    for(i=0;imalloc(sizeof(struct info));
        info_table[i]->distance=MAX;
        info_table[i]->before=-1;
        info_table[i]->sign=0;
    }
    info_table[vertex]->distance=0;
    //入度为零的节点入队列
    for(i=0;iif(Indegree[i]==0)
        {
            queue[rear]=i;
            rear++;
        }
    }
    int curr;
    Node temp;
    int new_len;
    while(head!=rear)
    {
        curr=queue[head];
        head++;
        printf("%d",curr);
        info_table[curr]->sign=1;
        temp=g->table[curr]->next;
        while(temp!=NULL)
        {
            if(info_table[curr]->distance!=MAX)
            {
                new_len=info_table[curr]->distance+temp->weight;
                if(new_lennum]->distance)
                {
                    info_table[temp->num]->distance=new_len;
                    info_table[temp->num]->before=curr;
                }
            }
            Indegree[temp->num]--;
            if(Indegree[temp->num]==0)
            {
                queue[rear]=temp->num;
                rear++;
            }
            temp=temp->next;
        }
    }
    return info_table;
}

3.最大网络流. 首先，我们先描述一下网络流问题。流网络 G=(V,E) 是一个有向图，其中每条边 (u,v)∈E 均有一非负容量 c(u,v)≥0 ，如果 (v,u)∈E ,那么 c(u,v)=0 .流网络中有两个特别的顶点：源点s和汇点t。同时我们假设每个顶点是出在从源点到汇点的一条路径上。 G 的流是一个实值函数 f:V∗V→R ,某个边上的流不超过这个边的容量。我们的问题就是寻找从s到t的最大值流，也就是求一个流函数，使得下式最大

∑v,(v,t)∈Ef(v,t)

基本的算法就是Ford-Fulkerson方法，我们借用《算法导论》中的伪代码来说明

for each edgd(u,v) in E
{
    do f[u,v]=0
       f[v,u]=0
}
while there exists a path p from s to t in the residual network Gf
{
    do cf(p)=min{cf(u,v):(u,v) is in p}
    for each edge(u,v) in p
    { 
        do f[u,v]=f[u,v]+cf(p)
           f[v,u]=-f[u,v]
    }
}      

代码的1-5行是对流函数f的初始化，代码的第六行出现了一个残余网络的概念 (residualnetwork) ,它是针对当前的邻接矩阵（也就是一个网络流图写成矩阵的形式），当前的流函数 f ，给出每条边 （u，v） 的剩余流量 cf(u,v)=c(u,v)−f(u,v) ,顶点是不变的图。在这样的一个残余网络中寻找从 s 到 t 的一条增广路 p ，其实也就是一条从 s 到 t 的路径，路径上的边的值大于零。代码的第7行是找到这条增广路径上边的最小剩余流量记为 cf(p) ，然后代码的第8-11行就是对流函数的更新，对于 p 上的每一条边 (u,v) ，更新其流量;对于这条路径上的反向边 (v,u) ,也更新其流量,这样做的目的是为了得到下一个残余网络，然后对下一个残余网络做相同的处理，直到残余网络中没有增广路径为止。那么每次的 cf(p) 的和就是我们所要求的最大流值。
针对上述代码的8-11行，我们可以将它和下一个剩余网络的生成进行合并，也就是针对当前的剩余网络，我们把路径 p 上的边，以及这些边的逆边做如下更新

cf(u,v)=cf(u,v)−cf(p)

cf(v,u)=cf(p)

那么现在最大的问题就是如何在剩余网络中寻找增广路径了。这时候就轮到 E−K 算法出场了， E−K 算法只是解决了如何寻找增广路径问题，它是对Ford-Fulkerson方法进一步具体化。
Edmonds-Karp算法. 算法实际上就是采用广度优先搜索来实现对增广路径的p的计算。具体的代码如下：

int E_K(int _start,int _end,vector<vector<int> > &adj_matrix,int before[],int n)
{
    queue<int> que;//队列，用于BFS
    vector<int> sign(n,0);//表示节点是否已经处理

    int temp;
    int i;
    que.push(_start);
    sign[_start]=1;

    while(!que.empty())
    {
        temp=que.front();
        que.pop();
        for(i=0;iif(adj_matrix[temp][i]>0&&sign[i]==0)
            {
                before[i]=temp;
                sign[i]=1;//注意
                if(i==_end) return 1;
                que.push(i);
            }
        }
    }
    return 0;
}

注：该函数中包含的参数有个before，主要是用来记录搜索到的增广路径的。 start 和 end 分别表示源点和汇点。

然后我们针对如下图的一个实例来实现 Ford−Fulkerson 算法。

代码如下：

int F_F(int _start,int _end,vector<vector<int> > &adj_matrix,int n)
{
    int max_flow=0;
    int path[n];
    int arg_path=E_K(_start,_end,adj_matrix,path,n);
    while(arg_path)
    {
        //找到增广路径上的边的最小流量
        int _min=1<<30;
        int next=_end;
        while(next!=_start)
        {
            if(adj_matrix[path[next]][next]<_min)
                _min=adj_matrix[path[next]][next];
            next=path[next];
        }
        //对邻接矩阵进行更新
        next=_end;
        while(next!=_start)
        {
            adj_matrix[path[next]][next]-=_min;
            adj_matrix[next][path[next]]=_min;
            next=path[next];
        }
        max_flow+=_min;
        arg_path=E_K(_start,_end,adj_matrix,path,n);
    }
    return max_flow;
}

4.最大生成树
最大生成树研究的对象是无向有权图，最小生成数就是连接图中所有的点的边构成的树，并且其权值最小。我们针对连通图来说明两种实现的算法。
算法1.Prim
1.设一个集合 S
2.构造一个信息表，记录所有顶点的一下三项信息：（1）是否被处理 sign，（2）到集合S的最短距离distance，（3）它的上一个顶点before。信息表初试化为，处理状态为0，到集合S的距离为无穷大，上一个顶点为-1。
3.选择一个顶点，更新它的distance为0。
4.选择distance最小的点a，更新它在信息表中的信息，处理状态为1，到集合S的最小距离为distance，然后将它放入集合S中。
5.更新a的邻点到S的最短距离以及它们的before为a，转到步骤4。
代码如下：

int min(int x,int y)
{
    return x>y?y:x;
}
struct node
{
    int num;
    int weight;
    struct node *next;
};
typedef struct node * Node;

struct graph
{
    int node_num;
    Node *table;
};
typedef struct graph * Graph;
struct info
{
    int distance;//表示到特定的s点的最短路径长度
    int before;//表示这个点的上一个顶点
    int sign;//是否已经被处理
};
typedef struct info *Info;

int find_min(Info *info_list,int n)
{
    int i;
    int min_dis=MAX;
    int min_vertex;
    for(i=0;iif(info_list[i]->distancesign==0)
        {
            min_dis=info_list[i]->distance;
            min_vertex=i;
        }
    }
    if(min_dis==MAX)
        return -1;
    return min_vertex;
}

Info *Prim(Graph g)
{
    int n=g->node_num;
    Info * info_list=malloc(sizeof(Info)*n);
    int i;
    for(i=0;istruct info));
        info_list[i]->distance=MAX;
        info_list[i]->before=-1;
        info_list[i]->sign=0;
    }
    info_list[0]->distance=0;
    Node temp;
    int adj_node;
    int min_vertex;
    for(;;)
    {
        min_vertex=find_min(info_list,n);
        if(min_vertex==-1)
            break;
        info_list[min_vertex]->sign=1;
        temp=g->table[min_vertex]->next;
        while(temp!=NULL)
        {
            adj_node=temp->num;
            if(info_list[adj_node]->sign==0&&info_list[temp->num]->distance>temp->weight)
            {
                info_list[temp->num]->distance=temp->weight;
                info_list[temp->num]->before=min_vertex;
            }
            temp=temp->next;
        }
    }
    return info_list;
}

算法4.2.Kruskal算法
Kruskal算法
1.对所有的边进行从大到小排序，排序依据是它的权重。
2.将图中所有的边去掉，只剩下点
3.然后选择最小权重的边，加入图中，看是否形成圈，如果没有就添加进去，否则就丢掉。重复3步骤直到添加的边数为点数减1.

注:持续实现选择最小边的数据结构是用优先队列，而将边添加到图中是不相交集的思想（不相交集ADT）

代码如下：

#include 
#include
#include
using namespace std;
//优先队列中的元素
struct edge
{
    int Start;
    int End;
    int weight;
};
//对这种边结构体进行比较
bool operator <(edge e1,edge e2)
{
    if(e1.weightreturn true;
    else
        return false;
}

struct cmp
{
    bool operator()(edge a,edge b)
    {
        if(a.weight>b.weight) return 1;
        return 0;
    }
};

int Find(vector<int> dis_set,int u)
{
    if(dis_set[u]<0)
        return u;
    else
        return Find(dis_set,dis_set[u]);
}
vector<int> kruskal(priority_queuevector,cmp> p,int n)
{
    //定义不相交集,每个单元表示一个类
    int total_edge=0;
    vector<int> disjset(n,-1);
    while(total_edgeint U=temp.Start;
        int V=temp.End;
        int U_root=Find(disjset,U);
        int V_root=Find(disjset,V);
        if(U_root!=V_root)
        {
            if(disjset[U_root]//union
            else
                disjset[U]=V;
            total_edge++;
        }
    }
    return disjset;
}

主函数如下：

int main()
{
    int adj_matrix[7][7]={{0,2,4,1,0,0,0},
                         {2,0,0,3,10,0,0},
                         {4,0,0,2,0,5,0} ,
                         {1,3,2,0,7,8,4} ,
                         {0,10,0,7,0,0,6},
                         {0,0,5,8,0,0,1} ,
                         {0,0,0,4,6,1,0}
                        };
    int i,j;

    priority_queue<edge,vector<edge>,cmp> p_que;//关键
    for(i=0;i<7;i++)
    {
        for(j=i;j<7;j++)
        {
            if(adj_matrix[i][j]>0)
            {
               edge new_e;
               new_e.Start=i;
               new_e.End=j;
               new_e.weight=adj_matrix[i][j];
               p_que.push(new_e);
            }
        }
    }
    vector<int> result=kruskal(p_que,7);
    for(i=0;i<7;i++)
    {
        if(result[i]>0)
            cout<<"("<<i<<","<<result[i]<<")"<<endl;
    } 
    return 0;
}