2019暑训 线段树学习笔记（未完待续

线段树

洛谷日报：Senior Data Structure · 浅谈线段树（Segment Tree）

讲道理线段树的模版也没有很长…之前看到说起码150行？总而言之比起前几天的WA自动机、筛法还是简单很多的…

建树

#define itn int
const int maxn = 1e5 + 5;

int a[maxn];
ll seg[maxn << 2];
int tag[maxn << 2];

inline itn ls(itn p){return p << 1;}
inline itn rs(int p){return (p << 1)|1;}

void pushup(int p){
    seg[p] = seg[ls(p)] + seg[rs(p)];
}

void build(int p, int l, int r){
    if(l == r){
        seg[p] = a[l];
        return ;
    }
    
    itn middle = (l + r) >> 1;
    build(ls(p), l, middle);
    build(rs(p), middle + 1, r);
    pushup(p);
}

建树这一部分的代码还是比较好理解的。
多用（但不要滥用）inline和位运算可以一定程度上降低时间复杂度

区间修改

void f(int p, int l, int r, int k){
    tag[p] += k;
    seg[p] += (r - l + 1) * 1ll * k;
    return ;
}

void pushdown(int p, int l, int r){
    int middle = (l + r) >> 1;
    f(ls(p), l, middle, tag[p]);
    f(rs(p), middle + 1, r, tag[p]);
    tag[p] = 0;
}

void update(int nl, int nr, int l, int r, int p, int k){
    if(nl <= l && r <= nr){
        seg[p] += (r - l + 1) * 1ll * k;
        tag[p] += k;
        return;
    }
    pushdown(p, l, r);
    int mid = (l + r) >> 1;
    if(nl <= mid) update(nl, nr, l, mid, ls(p), k);
    if(nr > mid) update(nl, nr, mid + 1, r, rs(p), k);
    pushup(p);
}

主函数是update函数，表示区间[nl; nr]进行加上k的更新操作，目前更新到p结点、区间为[l; r]。
如果当前的区间完全被更新的区间包含，那么更新线段树seg的值、记录tag标记即可。
如果当前的区间与更新的区间有重叠，那么我们分而治之、寻找子区间来拼凑出需求的更新区间。

这里的pushdown其实比较让人疑惑。我的理解还不是很到位。
可以料想到的是，刚开始的tag都是0，只有某一次出现了 完全包含 的情况，tag才可能发生变化，之后再由pushdown函数从父结点向儿子结点发生转移，完成孩子线段树的更新。言下之意也就是，如果某一段区间具有非0的tag值，那么这一段区间的某个祖先一定是被完全更新的，那么该孩子区间需要更新也就毋庸置疑了。

查询

ll query(int nl, int nr, int l, int r, int p){
    ll res = 0;
    if(nl <= l && r <= nr){
        res += seg[p]; return res;
    }
    pushdown(p, l, r);
    int mid = (l + r) >> 1;
    if(nl <= mid) res += query(nl, nr, l, mid, ls(p));
    if(nr > mid) res += query(nl, nr, mid + 1, r, rs(p));
    return res;
}

看到查询操作的代码，又是这个 pushdown函数 格外引人注目。
为什么在查询的时候也需要不断的更新tag呢？？
那我们回头看修改操作的代码，可以发现，当父亲结点往下传tag的时候，父亲的seg值被修改，但是孩子们仅仅是继承了tag，孩子的seg值尚且没有发生变化。只有当往孩子传tag的时候，我们才会修改该结点的seg值。而因为我们的修改操作不一定能覆盖某个父亲所有的孩子，所以也就不是所有的tag都能在修改操作中发生传递，有一些会暂时的保留在结点上。
那么这样子分析后，也就不难理解为什么query的时候也需要对tag进行传递、修改结点seg值了。
不愧是lazy tag，如果没有被修改、查询到的话，就会一直赖在结点上不肯走啊。

附上两道洛谷模版题

1 区间加法修改，区间查询： 洛谷 P3373 【模版】 （附上 AC代码

2 区间加法、乘法修改，区间查询： P3373 【模板】线段树 2
尝试用两个tag分别记录sum和multi，但是在pushdown的时候只是很朴素的把（sum * (r- l + 1) + sg[p]) *multi…尽管这个问题最开始我就有怀疑了，但是当时不知道怎么的觉得这样子可能是对的就开始写了…后来发现是算法假了。因为➕和✖️的顺序未知，所以不可以朴素的相加相乘。
那还能怎么办嘛…看题解啦…
题解 P3373 【【模板】线段树 2】
比较有道理的地方在于，规定了加法、乘法的优先级，从而等价地维护了线段树的真值。可以考虑到的是，如果先乘后加，只需要把之前的stag乘上当前的系数再加上新的s即可。而如果先加后乘，为了维护线段树的真值，系数mtag会“联动”成一个很不漂亮的小数，从各个意义上来看都是不够好的。

千辛万苦后终于AC，附上代码 R23129360 记录详情
我饱含泪水行行对比，不觉得我自己的线段树代码有问题，事实上是，线段树果然是没问题的。
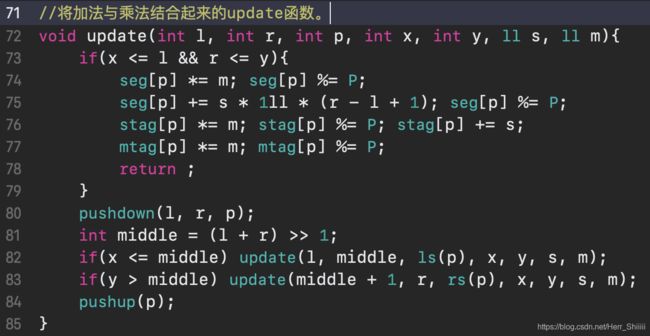但是！乘法的单位元是1，需要手动初始化！！！（根据上述update函数可知，区间加法的时候修改s，m取1；区间乘法的的时候修改m，s取0）
初始化也没毛病，我考虑到了。
⚠️但是我万万没考虑到线段树的初始化要初始化到4n！！4n！！太坑了，以后不能忘了！
至此总算AC。

权值线段树与主席树

权值线段树的代码其实很朴素，能够实现的功能也比较局限。
权值线段树可以完成单点修改以及查询某一段连续桶中的个数和（特别地，当连续的长度为1时，就是统计某一个数在整个序列中出现的次数）。

但是当我们想要完成若干次的区间查询第k大的时候，使用权值线段树显然是一个非常粗糙的办法，从而 可持久权值线段树（即主席树） 就应运而生了。