基本数据结构

基本数据结构

C

	//顺序表
	typedef int ElemType;
	typedef struct
	{
		ElemType data[MAXSIZE];
		int length;		//当前顺序表的实际长度
	}Sqlist
	//单链表
	typedef struct Node
	{
		ElemType data;
		struct Node *next;
	}Node;
	//双向链表
	typedef struct DulNode
	{
		ElemType data;
		struct DulNode *prior;
		struct DulNode *next;
	}DulNode,*DuLinkList;
	//顺序栈
	typedef struct
	{
		ElemType data[MAXSIZE];
		int top; 	//用于栈顶指针
	}SqStack;
	//两顺序栈共享空间结构
	typedef struct
	{
		ElemType data[MAXSIZE];
		int top1;
		int top2;
	}SqDoubleStack;
	//链栈
	typedef struct StackNode
	{
		ElemType data;
		struct StackNode *next;
	}StackNode,*LinkStackPtr;
	typedef struct LinStack
	{
		LinkStackPtr top;
		int count;
	}LinkStack;
	//循环队列的顺序存储结构，当前长度 = (rear-front+QueueSize)%QueueSize
	typedef struct
	{
		ElemType data[MAXSIZE];
		int front;
		int rear;
	}SqQueue;
	//队列的单链存储结构
	typedef struct QNode
	{
		ElemType data;
		struct QNode *next;
	}QNode,*QueuePtr;
	typedef struct
	{
		QueuePtr front,rear;
	}LinkQueue;

C++

不同容器有共同性，pop都是弹出，会删除容器内的元素，vector和deque可以用[ ]运算符。

栈：后进先出，顺序结构

#include//栈
stack<int>  s;//参数也是数据类型，这是栈的定义方式
s.empty()//如果栈为空返回true，否则返回false  
s.size()//返回栈中元素的个数  
s.pop()//删除栈顶元素但不返回其值  
s.top()//返回栈顶的元素，但不删除该元素  
s.push(X)//在栈顶压入新元素 ，参数X为要压入的元素
//
#include 	//可以像数组一样操作，删除非末尾数据代价大
vector<int> v;
v.front();	//取第一个元素
v.back();	//取最后一个元素
v.begin();	//取第一个迭代器，迭代器可以理解成容器的基本单位，是一个含有其他成员函数的结构体。
v.end();		//尾后迭代器
v.push_back(elem);	//压栈
v.pop_back();	//出栈
v.erase(pos);	//删除pos位元素，效率底

队列：先进先出，顺序结构，从首尾进出效率高，插入效率底

#include// 队列，单进单出：尾进头出
queue<int>  q; //参数是数据类型，这是队列的定义方式
q.empty()// 如果队列为空返回true，否则返回false  
q.size() // 返回队列中元素的个数  
q.pop()  //删除队列首元素但不返回其值  
q.front()  // 返回队首元素的值，但不删除该元素  
q.push(X) //在队尾压入新元素 ，X为要压入的元素
q.back() //返回队列尾元素的值，但不删除该元素
//
#include 	//包含vector的所有操作，双进双出
deque<int> dq;
dq.push_front();	//头部入队
dq.pop_front();	//头部出队

链表：两头进出，顺序结构,不能返回指定元素，不能用[ ]运算符

#include 	//双向链表
list<int> l;	//定义
l.empty();
l.size();
l.push_back(elem);
l.pop_back();
l.push_front();
l.pop_front();
l.insert(l.begin()+2, 3, 6);	//不能直接定位位置，只能从两端迭代，在首位+2前面，插入3个6
							//如果原来是1 2 3 4 5 6，则变成1 2 6 6 6 3 4 5 6
l.erase(++l.begin());	//删除第二个元素

树

节点的度： 孩子的个数；
有序树： 每个节点的孩子是有序的树，顺序不同代表不同的树；
无序树： 节点的孩子顺序不同代表的是相同的树。
二叉树： 所有的节点，度均为2；但是左孩子或者右孩子可以缺失一个，不缺失的称为满二叉树；如果每个叶节点的深度相同，就是完全二叉树，内部节点个数为(h是最大深度)：$$2^h-1$$

由数组构造树，应先进行排序，这样生成的才是一个最优二叉树
如何遍历一颗二叉搜索树来按序输出各个值
每个节点都有关键字，按照关键字大小的设置顺序从小到大遍历分为三种情况：
中序遍历：left.key < root.key < right.key
先序遍历：root.key < left.key < right.key
后序遍历：left.key < right.key < root.key
遍历时间是n。
如何在一颗二叉搜索树上查找一个值
以中序遍历为例，要查询的关键字与节点关键字比较，小于查左边，大于查右边。
如何查找最小或最大元素
如最小值：min.left == nil 那么一直循环，不断往左查询，直到left=nil；最大值就一直往右查询。
如何查找一个元素的 前驱 和 后继
前驱：比关键字小的最大值。查询左树的最大值。
后继：比关键字大的最小值。查询右树的最小值。
表示方法

//Definition for a binary tree node.
struct TreeNode {
     int key;
     TreeNode *left;
     TreeNode *right;
     TreeNode *parent;
     TreeNode(int x) : val(x), left(NULL), right(NULL), parent(null) {}
 };	

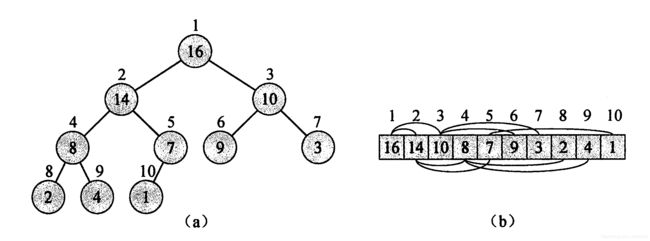
用数组表示，则规定：除了底层外，该树是完全二叉树，根节点为A[0]，每层从左向右给定下标，深度依次加深，这样可以将一个数组还原成一颗二叉树。

实用的操作

#include 
#include 
using namespace std;

struct TreeNode {
    int key;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : key(x), left(nullptr), right(nullptr) {}
};
//按照中序遍历构造二叉树
TreeNode* sortedArrayToBST(vector<int>& nums, int l, int r)
{
    if(r < l)   //l=0,r=0则只有一个元素，没有排序的必要
        return nullptr;
    int mid = l+(r-l)/2;
    TreeNode *root = new TreeNode(nums[mid]);
    root->left = sortedArrayToBST(nums,l,mid-1);
    root->right = sortedArrayToBST(nums,mid+1,r);
    return root;
}
TreeNode* sortedArrayToBST(vector<int> &nums)   //构造二叉树
{
    return sortedArrayToBST(nums, 0, nums.size()-1);
}
void midPrint(TreeNode *tree)   //前序遍历 打印
{
    if(tree == nullptr)
        return;
    cout << tree->key << endl;
    midPrint(tree->left);
    midPrint(tree->right);

}
int minNode(TreeNode *tree)     //最小节点
{
    if(tree->left == nullptr)
        return tree->key;
    return minNode(tree->left);
}
int main()
{
    vector<int> nums = {-10,-3,0,5,9,11,};
    for(auto i : nums)
        cout << i << " ";
    cout << endl;
    TreeNode *root = sortedArrayToBST(nums);
    midPrint(root);
    cout << "最小值：" << minNode(root) << endl;
    cout << "后继：" << minNode(root->right) << endl;
    return 0;
}

前、中后序遍历的区别

前序遍历先处理节点，再一次处理左右孩子
中序遍历先处理左孩子，把节点处理放在中间，再处理右孩子
后序遍历依次先处理左右孩子，最后处理节点
适用的场合
二叉树应用非常广泛。首先二叉树是树的基础，利用二叉树可以构造树和森林。在操作系统源程序中，树和森林被用来构造文件系统。我们看到的window和linux等文件管理系统都是树型结构。在编译系统中，如C编译器源代码中，二叉树的中序遍历形式被用来存放C 语言中的表达式。在游戏设计领域，许多棋类游戏的步骤都是按树型结构编写。其次二叉树本身的应用也非常多，如哈夫曼二叉树用于JPEG编解码系统（压缩与解压缩过程）的源代码中，甚至于编写处理器的指令也可以用二叉树构成变长指令系统，另外二叉排序树被用于数据的排序。