hdu4315 Climbing the Hill(阶梯博弈)
Climbing the Hill
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1218 Accepted Submission(s): 548
Problem Description
Alice and Bob are playing a game called "Climbing the Hill". The game board consists of cells arranged vertically, as the figure below, while the top cell indicates the top of hill. There are several persons at different cells, and there is one special people, that is, the king. Two persons can't occupy the same cell, except the hilltop.
At one move, the player can choose any person, who is not at the hilltop, to climb up any number of cells. But the person can't jump over another one which is
above him. Alice and Bob move the persons alternatively, and the player who move the king to the hilltop will win.
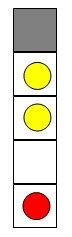
Alice always move first. Assume they play optimally. Who will win the game?
At one move, the player can choose any person, who is not at the hilltop, to climb up any number of cells. But the person can't jump over another one which is
above him. Alice and Bob move the persons alternatively, and the player who move the king to the hilltop will win.

Alice always move first. Assume they play optimally. Who will win the game?
Input
There are several test cases. The first line of each test case contains two integers N and k (1 <= N <= 1000, 1 <= k <= N), indicating that there are N persons on the
hill, and the king is the k-th nearest to the top. N different positive integers followed in the second line, indicating the positions of all persons. (The hilltop is No.0 cell, the cell below is No.1, and so on.) These N integers are ordered increasingly, more than 0 and less than 100000.
hill, and the king is the k-th nearest to the top. N different positive integers followed in the second line, indicating the positions of all persons. (The hilltop is No.0 cell, the cell below is No.1, and so on.) These N integers are ordered increasingly, more than 0 and less than 100000.
Output
If Alice can win, output "Alice". If not, output "Bob".
Sample Input
3 3 1 2 4 2 1 100 200
Sample Output
Bob Alice
Hint
The figure illustrates the first test case. The gray cell indicates the hilltop. The circles indicate the persons, while the red one indicates the king. The first player Alice can move the person on cell 1 or cell 4 one step up, but it is not allowed to move the person on cell 2.
Author
TJU
Source
2012 Multi-University Training Contest 2
题意】
有N个人爬山,山顶坐标为0,其他人的坐标按升序给出。不同的坐标只能容纳一个人(山顶不限),Alice和Bob轮流选择一个人让他移动任意步,但不能越过前面那个人。现在有一个人是king(给出id),谁能将king移动到山顶就算赢。
【分析】
考虑King的情况和上述版本几乎一致,只要把King当作普通人一样处理即可。
除了两种特殊情况:
1. 当King是第一个人时,Alice直接胜
2. 当King是第二个人且一共有奇数个人时,第一堆的大小需要减1。
因为如果king在奇数石子上,那么king前面的那一对石子k1,k2.
当对方把k1移到top时,我可以把k2移到top前的一个位置.
那么对于k2石子,对方如果碰了它,那么我肯定会把king移到top的.
所以k2也相当于是一颗废子而已,不影响最终Nim的结果.
Ps:阶梯博弈学习博客链接:阶梯博弈
#pragma comment(linker, "/STACK:102400000,102400000")
#include
#include
#include
#include
#include
#include