智能交通 | 邻接矩阵 | Dijkstra | 最优路径
编写程序,实现智能交通中的最佳路径选择问题:设有n个地点,编号为0→n-1,m条路径的起点、终点和代价由用户输入提供,使用 [邻接表] 邻接矩阵为存储结构,寻找最佳路径方案(如花费时间最少,路径长度最短,交通费用最少等问题任选其一即可)
为什么用的是邻接矩阵?
没有为什么,看错题目了。。。。:)
codeblocks中报错:‘to_string’ was not declared in this scope解决方案:
https://blog.csdn.net/haofandedaima/article/details/90137837#commentBox
char转string
#include 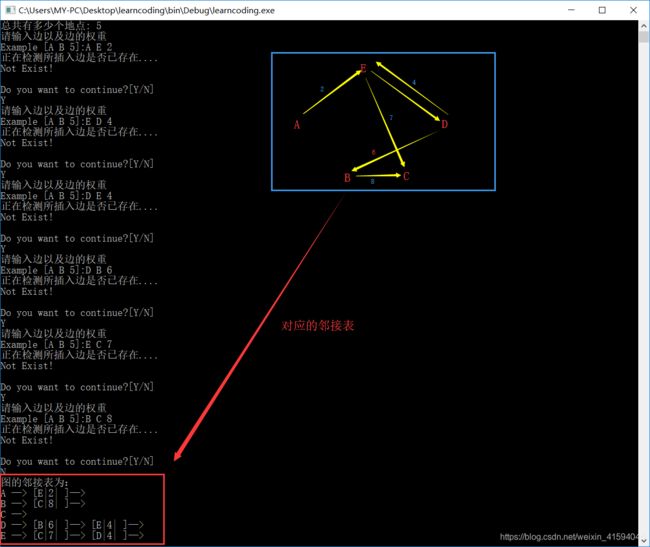
ITS.cpp [ Intelligent Transportation System ]
#include Dijkstra.h
#pragma once
//#pragma once是一个比较常用的C/C++杂注,
//只要在头文件的最开始加入这条杂注,
//就能够保证头文件只被编译一次。
#includeDijkstra.cpp
#include"Dijkstra.h"
//构造函数
Graph_DG::Graph_DG(int vexnum, int edge) {
//初始化顶点数和边数
this->vexnum = vexnum;
this->edge = edge;
//为邻接矩阵开辟空间和赋初值
arc = new int*[this->vexnum];
dis = new Dis[this->vexnum];
for (int i = 0; i < this->vexnum; i++) {
arc[i] = new int[this->vexnum];
for (int k = 0; k < this->vexnum; k++) {
//邻接矩阵初始化为无穷大
arc[i][k] = INT_MAX;
}
}
}
//析构函数
Graph_DG::~Graph_DG() {
delete[] dis;
for (int i = 0; i < this->vexnum; i++) {
delete this->arc[i];
}
delete arc;
}
// 判断我们每次输入的的边的信息是否合法
bool Graph_DG::check_edge_value(int start, int end, int weight) {
if (start<1 || end<1 || start>vexnum || end>vexnum || weight < 0) {
return false;
}
return true;
}
void Graph_DG::createGraph() {
cout << "请输入每条边的起点和终点以及其权重:" << endl;
int start;
int end;
char start1;
char end1;
int weight;
int count = 0;
while (count != this->edge) {
cin >> start1 >> end1 >> weight;
//首先判断边的信息是否合法
start = int(start1 - 64);
end = int(end1 - 64);
while (!this->check_edge_value(start, end, weight)) {
cout << "输入的边的信息不合法,请重新输入" << endl;
cin >> start >> end >> weight;
}//对邻接矩阵对应上的点赋值
arc[start - 1][end - 1] = weight;
++count;
}
}
void Graph_DG::print() {
cout<<endl;
cout << "图的邻接矩阵为:" << endl;
int count_row = 0; //打印行的标签
int count_col = 0; //打印列的标签
while (count_row != this->vexnum) { //开始打印
count_col = 0;
while (count_col != this->vexnum) {
if (arc[count_row][count_col] == INT_MAX)
cout << "∞" << " ";
else
cout << arc[count_row][count_col] << " ";
++count_col;
}
cout << endl;
++count_row;
}
}
void Graph_DG::Dijkstra(int begin){
//初始化dis数组
int i;
for (i = 0; i < this->vexnum; i++) { //设置当前的路径
stringstream stream1,stream2;
stream1 << char(begin+64);
stream2 << char(i + 65);
dis[i].path =stream1.str() + "-->" + stream2.str();
dis[i].value = arc[begin - 1][i];
}
dis[begin - 1].value = 0; //设置起点的到起点的路径为0
dis[begin - 1].visit = true;
int count = 1;
//计算剩余的顶点的最短路径(剩余this->vexnum-1个顶点)
while (count != this->vexnum) {
//temp用于保存当前dis数组中最小的那个下标
//min记录的当前的最小值
int temp=0;
int min = INT_MAX;
for (i = 0; i < this->vexnum; i++) {
if (!dis[i].visit && dis[i].value<min) {
min = dis[i].value;
temp = i;
}
}
//把temp对应的顶点加入到已经找到的最短路径的集合中
dis[temp].visit = true;
++count;
for (i = 0; i < this->vexnum; i++) {
stringstream stream3;
if (!dis[i].visit && arc[temp][i]!=INT_MAX && (dis[temp].value + arc[temp][i]) < dis[i].value) {
//注意这里的条件arc[temp][i]!=INT_MAX必须加,不然会出现溢出,从而造成程序异常
dis[i].value = dis[temp].value + arc[temp][i];
//如果新得到的边可以影响其他为访问的顶点,那就就更新它的最短路径和长度
stream3 << char(i + 65);
dis[i].path = dis[temp].path + "-->" + stream3.str();
}
}
}
}
void Graph_DG::print_path(int begin) {
string str;
str =char(begin+64);
cout<<endl;
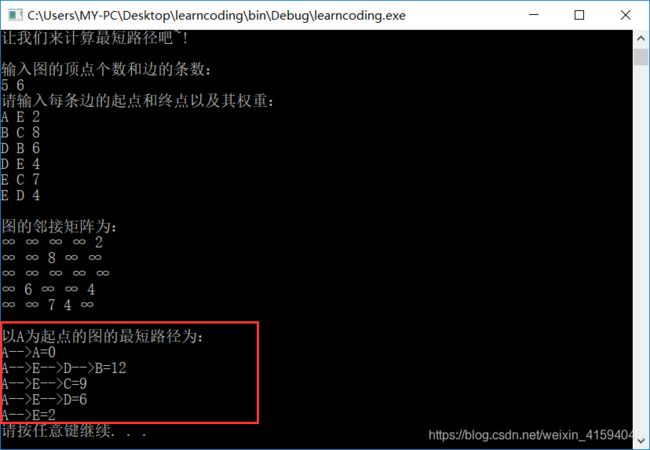
cout << "以"<<str<<"为起点的图的最短路径为:" << endl;
for (int i = 0; i != this->vexnum; i++) {
if(dis[i].value!=INT_MAX)
cout << dis[i].path << "=" << dis[i].value << endl;
else {
cout << dis[i].path << "无最短路径" << endl;
}
}
}