算法:凸多边形最优三角剖分
1、问题相关定义:
(1)凸多边形的三角剖分:将凸多边形分割成互不相交的三角形的弦的集合T。
(2)最优剖分:给定凸多边形P,以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分,使得该三角剖分中诸三角形上权之和为最小。
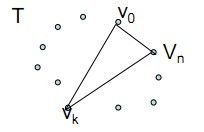
凸多边形三角剖分如下图所示:
2、最优子结构性质:
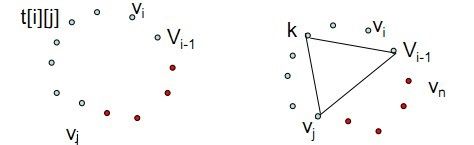
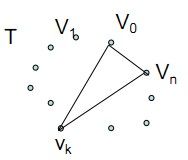
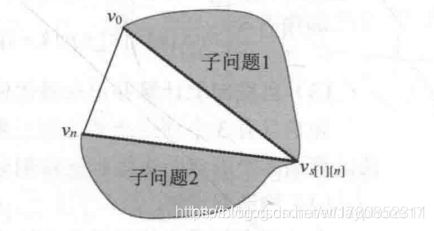
若凸(n+1)边形P={V0,V1……Vn}的最优三角剖分T包含三角形V0VkVn,1<=k<=n,则T的权为三个部分权之和:三角形V0VkVn的权,多边形{V0,V1……Vk}的权和多边形{Vk,Vk+1……Vn}的权之和。如下图所示:
可以断言,由T确定的这两个子多边形的三角剖分也是最优的。因为若有{V0,V1……Vk}和{V0,V1……Vk}更小权的三角剖分,将导致T不是最优三角剖分的矛盾。因此,凸多边形的三角剖分问题具有最优子结构性质。
3、递推关系:
设t[i][j],1<=i 因此,可得递推关系式:
凸(n+1)边形P的最优权值为t[1][n]。
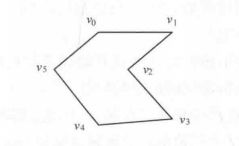
如下图所示,不是一个凸多边,因为v1v3连线落在了多边形的外部
凸多边形不相邻的两个顶点的连线称为凸多边形的弦
(2)什么是凸多边形的三角剖分?
凸多边形的三角剖分是指将一个凸多边形分割成互不相交的三角形的弦的集合。如下图所示,都是三角形的剖分,三角形的剖分有很多种:
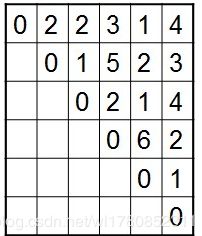
如果我们在给定凸多边形及定义在边,弦上的权值,即任意两点之间定义一个数值作为i权值,如图所示:
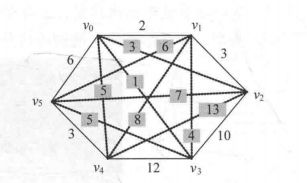
三角形上权值之和是指三角形的3条边上的权值之和:
w(vi vk vj)=|vi vk| + |vk vj | + |vi vj|
如图所示,w(v0v1v4)=|v0v1| + |v1v4| + |v0v4| = 22+8+5=15.
(3)什么是凸多边形最优三角剖分?
一个凸多边形的三角剖分有很多种,最优三角剖分就是划分的各三角形上权函数之和最小的三角剖分。
凸多边形最优三角剖分满足动态规划的最优子结构性质,可以从自底向上逐渐推出整体的最优。
(1)确定合适的数据结构
采用二维数组weight[ ][ ]记录各个顶点之间的连接权值,二维数组t[ ][ ]存放各个子问题的最优值,二维数组s[ ][ ]存放各个子问题的最优策略。
(2)初始化
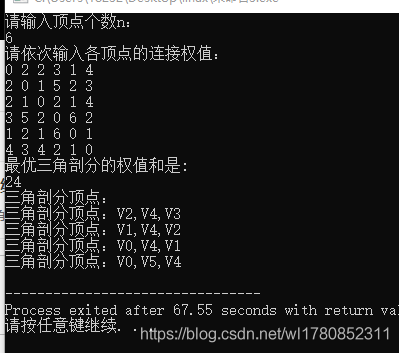
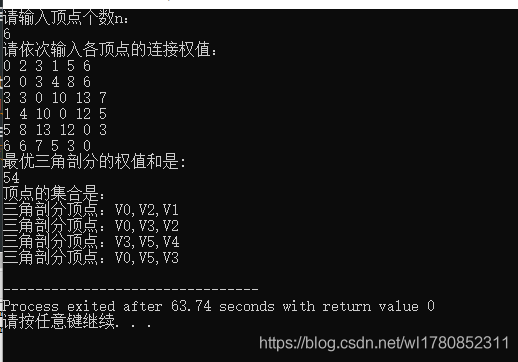
输入顶点数n,然后依次输入各个顶点之间的连接权值存储在二维数组weight[ ][ ]中,令n=n-1(顶点标号从v0开始),
t[i][i]=0,s[i][i]=0,其中i=1,2,3,4……,n-1。
(3)循环
按照递归关系式计算3个顶点{v i-1,vi,vi+1}的最优三角剖分,j=i+1,将最优值存入t[i][j],同时将最优策略存入s[i][j],i=1,2,3,……,n-1。
按照递归关系式计算4个顶点{v i-1,vi,vi+1,vi+2}的最优三角剖分,j=i+2,将最优值存入t[i][j],同时将最优策略存入s[i][j],i=1,2,3,……,n-2。
以此类推,直到求出所有顶点{v0,v1,v2,……,vn}的最优三角剖分,并将最优值存入t[1][n],将最优策略记入s[1][n]
(4)构造最优解
根据最优决策信息数组s[ ][ ]递归构造最优解,即输出凸多边形的最优剖分的所有弦。s[1][n],表示凸多边形最优三角剖分位置。
如果子问题1为空,即没有一个顶点,说明V0Vs[1][n]是一条边,不是弦,不需要输出,否则,输出该弦V0Vs[1][n]
如果子问题2为空,即没有一个顶点,说明Vs[1][n]Vn是一条边,不是弦,不需要输出,否则,输出该弦Vs[1][n]Vn
递归构造两个子问题{ v0,v1,v2,……,Vs[1][n] } 和 { Vs[1][n] ,v1,v2,……,vn },一直递归到子问题为空停止。
#include