Spark GraphX 中的 pregel函数

---

一篇关于 Spark GraphX 中 pregel函数 的笔记，通过一个小案例将pregel函数理解透彻。

• pregel函数源码 与 各个参数介绍：

---

  def pregel[A: ClassTag](
      initialMsg: A,
      maxIterations: Int = Int.MaxValue,
      activeDirection: EdgeDirection = EdgeDirection.Either)(
      vprog: (VertexId, VD, A) => VD,
      sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
      mergeMsg: (A, A) => A)
    : Graph[VD, ED] = {
    Pregel(graph, initialMsg, maxIterations, activeDirection)(vprog, sendMsg, mergeMsg)
  }

参数	说明
initialMsg	图初始化的时候，开始模型计算的时候，所有节点都会先收到一个消息
maxIterations	最大迭代次数
activeDirection	规定了发送消息的方向
vprog	节点调用该消息将聚合后的数据和本节点进行属性的合并
sendMsg	激活态的节点调用该方法发送消息
mergeMsg	如果一个节点接收到多条消息，先用mergeMsg 来将多条消息聚合成为一条消息，如果节点只收到一条消息，则不调用该函数

• 案例： 求顶点5 到 其他各顶点的 最短距离

---

在理解案例之前，首先要清楚关于 顶点 的两点知识：

1. 顶点 的状态有两种：
   (1)、钝化态【类似于休眠，不做任何事】
   (2)、激活态【干活】

2. 顶点 能够处于激活态需要有条件：
   (1)、成功收到消息 或者
   (2)、成功发送了任何一条消息
   
   

案例源码如下：

package com.hanwei.sparkgraphx01.helloworld
import org.apache.spark.{SparkConf, SparkContext}
import org.apache.spark.graphx._
import org.apache.spark.rdd.RDD

object Graphx06_Pregel extends App{

    //1、创建SparkContext
    val sparkConf = new SparkConf().setAppName("GraphxHelloWorld").setMaster("local[*]")
    val sparkContext = new SparkContext(sparkConf)

    //2、创建顶点
    val vertexArray = Array(
      (1L, ("Alice", 28)),
      (2L, ("Bob", 27)),
      (3L, ("Charlie", 65)),
      (4L, ("David", 42)),
      (5L, ("Ed", 55)),
      (6L, ("Fran", 50))
    )
    val vertexRDD: RDD[(VertexId, (String,Int))] = sparkContext.makeRDD(vertexArray)

    //3、创建边，边的属性代表 相邻两个顶点之间的距离
    val edgeArray = Array(
      Edge(2L, 1L, 7),
      Edge(2L, 4L, 2),
      Edge(3L, 2L, 4),
      Edge(3L, 6L, 3),
      Edge(4L, 1L, 1),
      Edge(2L, 5L, 2),
      Edge(5L, 3L, 8),
      Edge(5L, 6L, 3)
    )
    val edgeRDD: RDD[Edge[Int]] = sparkContext.makeRDD(edgeArray)


    //4、创建图（使用aply方式创建）
    val graph1 = Graph(vertexRDD, edgeRDD)

    /* ************************** 使用pregle算法计算 ，顶点5 到 各个顶点的最短距离 ************************** */

    //被计算的图中 起始顶点id
    val srcVertexId = 5L 
    val initialGraph = graph1.mapVertices{case (vid,(name,age)) => if(vid==srcVertexId) 0.0 else Double.PositiveInfinity}
    
    //5、调用pregel
    val pregelGraph = initialGraph.pregel(
    Double.PositiveInfinity,
    Int.MaxValue,
    EdgeDirection.Out
  )(
    (vid: VertexId, vd: Double, distMsg: Double) => {
      val minDist = math.min(vd, distMsg)
      println(s"顶点${vid}，属性${vd}，收到消息${distMsg}，合并后的属性${minDist}")
      minDist
    },
    (edgeTriplet: EdgeTriplet[Double,PartitionID]) => {
      if (edgeTriplet.srcAttr + edgeTriplet.attr < edgeTriplet.dstAttr) {
        println(s"顶点${edgeTriplet.srcId} 给 顶点${edgeTriplet.dstId} 发送消息 ${edgeTriplet.srcAttr + edgeTriplet.attr}")
        Iterator[(VertexId, Double)]((edgeTriplet.dstId, edgeTriplet.srcAttr + edgeTriplet.attr))
      } else {
        Iterator.empty
      }
    },
    (msg1: Double, msg2: Double) => math.min(msg1, msg2)
  )

  //6、输出结果
//  pregelGraph.triplets.collect().foreach(println)
//  println(pregelGraph.vertices.collect.mkString("\n"))

  //7、关闭SparkContext
  sparkContext.stop()
}

输出结果：

//------------------------------------------ 各个顶点接受初始消息initialMsg ------------------------------------------
顶点3，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点2，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点4，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点6，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点1，属性Infinity，收到消息Infinity，合并后的属性Infinity
顶点5，属性0.0，收到消息Infinity，合并后的属性0.0
//------------------------------------------ 第一次迭代 ------------------------------------------
顶点5 给 顶点6 发送消息 3.0
顶点5 给 顶点3 发送消息 8.0
顶点3，属性Infinity，收到消息8.0，合并后的属性8.0
顶点6，属性Infinity，收到消息3.0，合并后的属性3.0
//------------------------------------------ 第二次迭代 ------------------------------------------
顶点3 给 顶点2 发送消息 12.0
顶点2，属性Infinity，收到消息12.0，合并后的属性12.0
//------------------------------------------ 第三次迭代 ------------------------------------------
顶点2 给 顶点4 发送消息 14.0
顶点2 给 顶点1 发送消息 19.0
顶点1，属性Infinity，收到消息19.0，合并后的属性19.0
顶点4，属性Infinity，收到消息14.0，合并后的属性14.0
//------------------------------------------ 第四次迭代 ------------------------------------------
顶点4 给 顶点1 发送消息 15.0
顶点1，属性19.0，收到消息15.0，合并后的属性15.0
//------------------------------------------ 第五次迭代不用发送消息 ------------------------------------------

• pregel原理分析

---

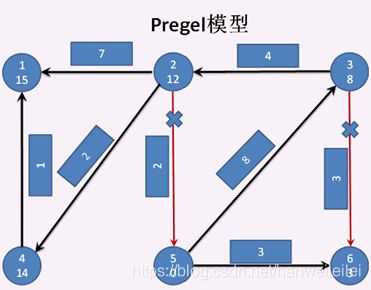
调用pregel方法之前，先把图的各个顶点的属性初始化为如下图所示：顶点5到自己的距离为0，所以设为0，其他顶点都设为 正无穷大Double.PositiveInfinity。见代码44行

当调用pregel方法开始：
首先，所有顶点都将接收到一条初始消息initialMsg ，使所有顶点都处于激活态（红色标识的节点）。

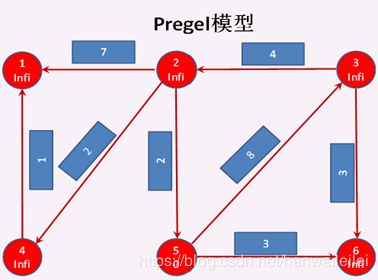
第一次迭代开始：

所有顶点以EdgeDirection.Out的边方向调用sendMsg方法发送消息给目标顶点，如果 源顶点的属性+边的属性<目标顶点的属性，则发送消息。否则不发送。
发送成功的只有两条边：
5—>3(0+8 5—>6(0+3 3—>2(Double.Infinity+4>Double.Infinity , 失败)
3—>6(Double.Infinity+3>Double.Infinity , 失败)
2—>1(Double.Infinity+7>Double.Infinity , 失败)
2—>4(Double.Infinity+2>Double.Infinity , 失败)
2—>5(Double.Infinity+2>Double.Infinity , 失败)
4—>1(Double.Infinity+1>Double.Infinity , 失败)。

sendMsg方法执行完成之后，根据顶点处于激活态的条件，顶点5 成功地分别给顶点3 和 顶点6 发送了消息，顶点3 和 顶点6 也成功地接受到了消息。所以 此时只有5，3，6 三个顶点处于激活态，其他顶点全部钝化。然后收到消息的顶点3和顶点6都调用vprog方法，将收到的消息 与 自身的属性合并。如下图2所示。到此第一次迭代结束。

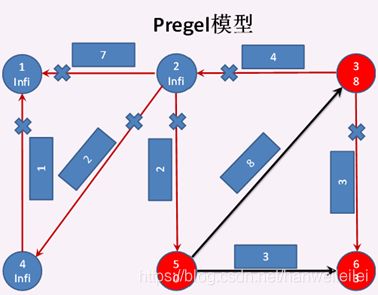
第二次迭代开始：
顶点3 给 顶点6 发送消息失败，顶点3 给 顶点2 发送消息成功，此时 顶点3 成功发送消息，顶点2 成功接收消息，所以顶点2 和 顶点3 都成为激活状态，其他顶点都成为钝化状态。然后顶点2 调用vprog方法，将收到的消息 与 自身的属性合并。 见图3. 至此第二次迭代结束。

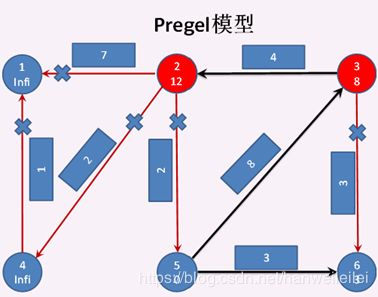
第三次迭代开始：
顶点3分别发送消息给顶点2失败 和 顶点6失败，顶点2 分别发消息给 顶点1成功、顶点4成功、顶点5失败 ，所以 顶点2、顶点1、顶点4 成为激活状态，其他顶点为钝化状态。顶点1 和 顶点4分别调用vprog方法，将收到的消息 与 自身的属性合并。见图4。至此第三次迭代结束

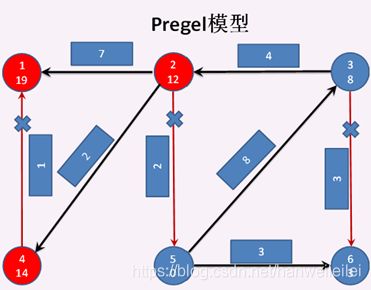
第四次迭代开始：
顶点2 分别发送消息给 顶点1失败 和 顶点4失败。顶点4 给 顶点1发送消息成功，顶点1 和 顶点4 进入激活状态，其他顶点进入钝化状态。顶点1 调用vprog方法，将收到的消息 与 自身的属性合并 。见图5

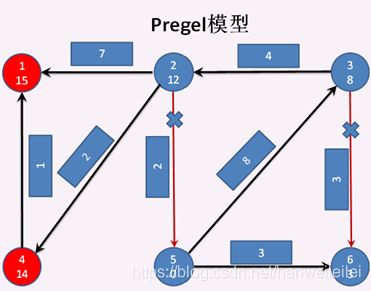
第五次迭代开始：
顶点4 再给 顶点1发送消息失败，顶点4 和 顶点1 进入钝化状态，此时全图都进入钝化状态。至此结束，见图6.