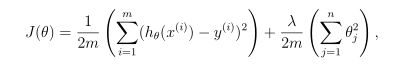机器学习---编程练习（五）：正则线性回归与偏差方差

机器学习—编程练习（五）：正则线性回归与偏差方差

文件清单

ex5.m - Octave/MATLAB script that steps you through the exercise
ex5data1.mat - Dataset
submit.m - Submission script that sends your solutions to our servers
featureNormalize.m - Feature normalization function
fmincg.m - Function minimization routine (similar to fminunc)
plotFit.m - Plot a polynomial fit
trainLinearReg.m - Trains linear regression using your cost function
[*] linearRegCostFunction.m - Regularized linear regression cost function
[*] learningCurve.m - Generates a learning curve
[*] polyFeatures.m - Maps data into polynomial feature space
[*] validationCurve.m - Generates a cross validation curve
* 表示需要做的内容

本次练习，你将会实现正则线性回归并且使用它学习不同偏差和方差的模型特性。由于这部分涵盖的知识方法很多，因此我会在这部分补充较多的内容。如果不需要看补充的知识，可以直接参考程序答案。
（待做）

1 正则线性回归

在练习的前半部分，你将会实现正则线性回归根据蓄水池水位预测水坝涌水量。在后半部分，你将通过调试诊断学习算法检查偏差方差的影响。

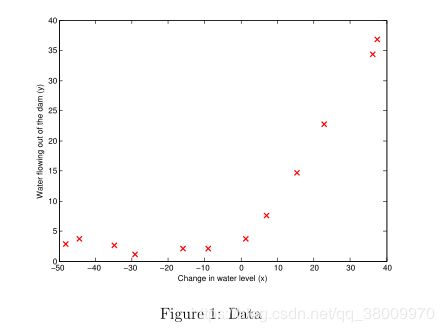
1.1 数据可视化

我们将从可视化数据开始。
历史记录中水位改变量为 x， 水坝溢水量为 y。
数据被分为3部分：
一个训练集，你的模型将会用它学习 ：X，y
一个交叉验证集，用于确定正则参数：Xval，yval
一个测试集，用于评估模型性能。这里有你的模型在训练过程中每见过的样本：Xtest, ytest

这3部分占整个数据的比例是 6：2：2

1.2 正则线性回归函数

函数公式：

1.3 正则化线性回归梯度

相对的，正则线性回归的对θ_j的偏导是

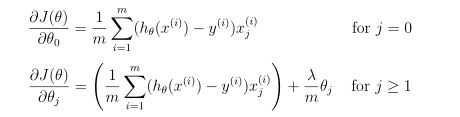
这部分很简单，实现上面的公式就可以了。

%这里之前计算矩阵间乘法的时候并没有加括号，但有时会出现错误。
%具体原因不明，为保险起见，之后都会添加括号
%X 12*2 theta 2*1 y 12*1 grad 2*1
h = X*theta; %12*1
theta_grad = theta;
theta_grad(1,:) = 0;
J = 1/(2*m) * ((h - y)' * (h - y)) + lambda/(2*m) * (theta_grad'*theta_grad);

%第一项不需要正则化
grad = 1/m * (X' * (h - y)) + lambda/m * theta_grad;

1.4 拟合线性回归

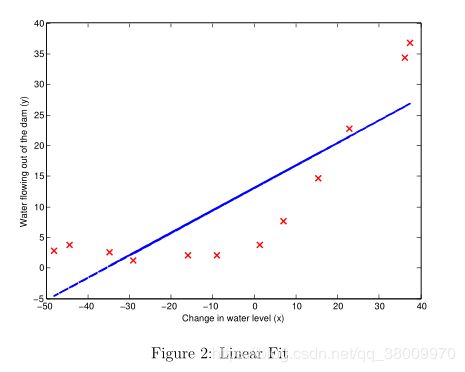
这部分没有什么需要特别解释的。但有一段话说明为什么需要绘制学习曲线，我将它翻译到了下面：
最优拟合直线告诉我们模型并不能很好的拟合数据，因为数据有一个非线性的图案。虽然可视化最优拟合是一种调试学习算法可行的方法，但是可视化数据和模型通常并不容易。在下一节中，你将会实现一个函数来绘制学习曲线，即使可视化数据并不容易，它也可以帮助你调试你的学习算法。

2 偏差方差

在机器学习中，有一个非常重要的概念是偏差与方差的权衡。高偏差的模型对于数据过于简单，不能很好的拟合数据，而高方差的模型则会对训练数据过拟合。
在下一部分的练习，你将会在一条学习曲线中绘制训练和测试误差，来诊断偏差方差问题。

2.1 学习曲线

回想一下，学习曲线将训练和交叉验证误差绘制为训练集大小的函数。 x：训练集大小 y：误差大小
你的工作是完成 learningCurve.m，它将会返回训练集和交叉验证集的误差向量。

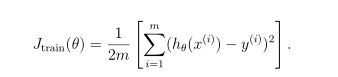
注意J_train是没有正则化项的

代码：

for i = 1:m
  
	X_train =  X(1:i, :);
	Y_train = y(1:i);
	theta = trainLinearReg(X_train,Y_train,lambda);
	%Jtrain没有正则化项，所以lambda为0
	error_train(i) = linearRegCostFunction(X_train,Y_train,theta,0);
	error_val(i) = linearRegCostFunction(Xval,yval,theta,0);
  
endfor

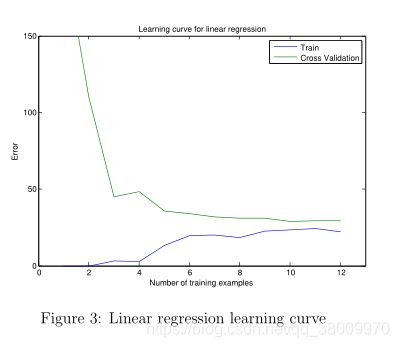
重要的是结论：
在Figure 3中，你可以观察到随着训练样本的增加，训练误差和交叉验证误差都非常高。
这反映了一个模型的高偏差问题——线性模型太简单了并且它不足以很好的拟合我们的数据。在下一节，你将会实现多项式回归为数据拟合一个更好的模型。

3 多项式回归

对于多项式回归，预测函数的格式

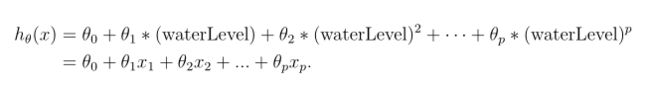
由此我们得到了一个特征是原始值的多次方的线性回归模型。
现在你将会使用数据的特征x的更高次幂，来添加更多的特征。你的任务是完成polyFeatures.m，函数将原始训练数据集X的大小 m1 映射成它的更高次幂。
当一个 m1 大小的训练数据集X传入到函数中，函数便返回一个 m*p 的矩阵X_poly，
X_poly的第一列是X的原始值，第二列是X .^ 2，第三列是X.^ 3，依此类推。

这里一个for循环搞定

for i = 1:p
  
  X_poly(:,i) = X.^i;
  
endfor

3.1 学习多项式回归

这是只摘取我认为比较重要的几句话。
注意即使在我们特征向量中有多项式项，我们仍然解决的是一个线性回归优化问题。多项式项仅仅转变成我们在线性回归使用的特征。我们使用同样的成本函数和梯度。
在这个练习中我们使用8项式，如果我们不进行特征归一化，特征将会有一个非常糟糕的比例尺。(40⁸ = 6.5x10¹²)
因此在为多项式回归学习参数θ之前，需要先特征归一化。

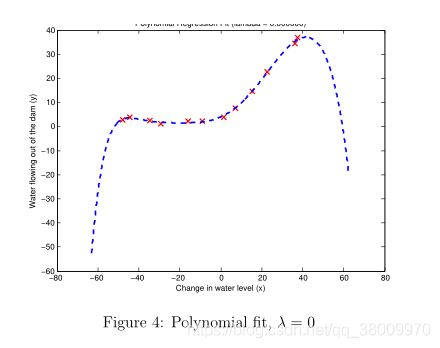
直接运行后，可以更观察到图4图5

结论：图4中，曲线经过了所有样本点，说明8次多项式对本次数据拟合的很好。但是，多项式拟合的非常复杂，甚至从极值落下。这表示多项式回归模型对训练数据过拟合，不能很好的表征数据的特征。
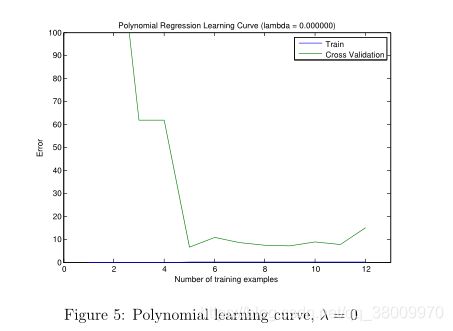
在图5中表示学习曲线低训练误差在较低的情况有相同的影响（
the learning curve (Figure 5) shows the same effect wherethe low training error is low
我猜测这句话的意思可能是说训练样本4之前都为0），但是交叉检验误差很高。
在训练和交叉误差之间有一个很大的间隔，这表示一个高方差问题。

3.2 选做：调整回归参数

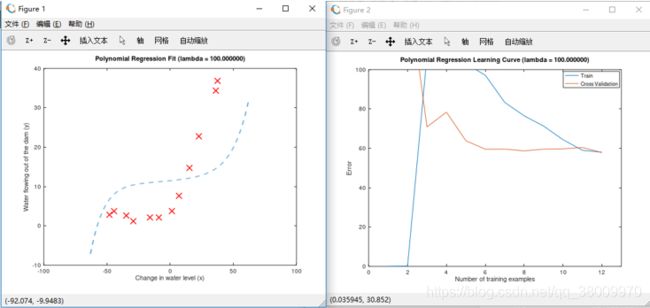
这部分没有需要修改脚本文件，但这部分能清楚的看到正则化的效果（之前做的都是未正则化的。 λ 设为0）
分别令 λ = 1， 100

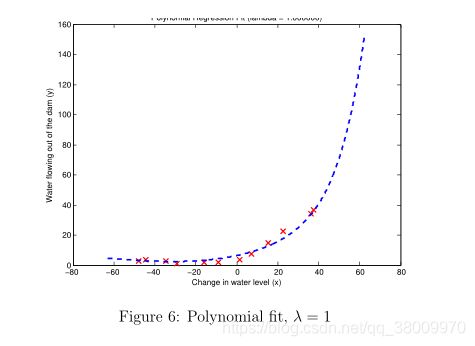
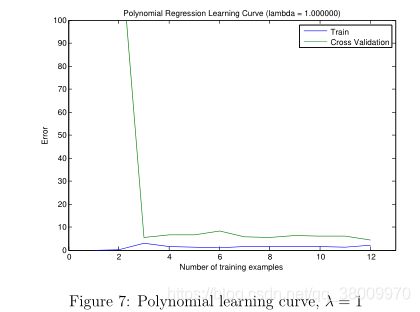
这是 λ = 1

下面这个是λ = 100，过分的正则化了，拟合的乱七八糟。

3.3 使用交叉验证集挑选λ

将λ的取值一 一带入线性回归成本函数中，求得各个交叉验证误差，找出最小的交叉验证误差。

for i = 1:length(lambda_vec)

   lambda = lambda_vec(i);
   theta = trainLinearReg(X, y, lambda);
   error_train(i) = linearRegCostFunction(X, y, theta, 0);
   error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);  
   
endfor

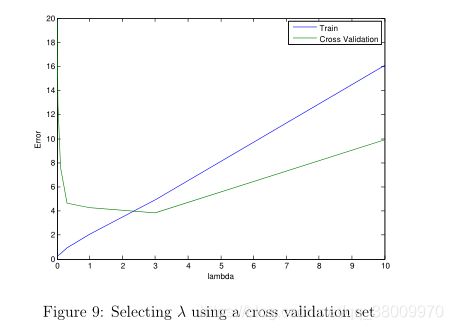
在本次练习中，交叉验证误差曲线中最小值是 lambda = 3

3.4 选做：计算测试训练误差

代码实现比较简单，需要注意的是这里使用的是多项式正则化后的数据（X_poly, y, X_poly_test, ytest），并不是原始数据。

%求出测试误差，评估模型在未知样本中的性能
function [error_test] = errorTest(X_poly, y, X_poly_test, ytest, lambda) 

   theta = trainLinearReg(X_poly, y, 3);
   [error_test, grad] = linearRegCostFunction(X_poly_test, ytest, theta, 0);
   fprintf('Compute Test Error (error_test = %f)\n\n', error_test);
   fprintf('Program paused. Press enter to continue.\n');
   pause;
   
end
 %怎么确定使用多少次项？
 %X_train ,y 得到的是theta值
 %X_val,y_val得到的是lambda值
 %最后使用X_test,y_test评估系统性能。
 %那么怎么确定使用多少次项才能很好的拟合数据呢？
 %每多一次项就多算一列的原始数据，找出合适的项就能节省运算资源。
 %留待以后解决。

之后调用函数就可以了。

3.5 选做：用随机挑选的样本绘制学习曲线

这个方法我不太喜欢，循环50次，迭代寻找theta最小200次，还有训练集大小12
总共需要计算50x12x200 120,000次，计算量太大了
代码参考链接：
https://blog.csdn.net/weixin_40597170/article/details/78990827