条件随机场(CRF)的原理与实现

一、概率无向图模型

模型定义

又称马尔科夫随机场。设有联合概率分布P(Y)，由无向图G=(V,E)表示，结点V表示随机变量，边E表示随机变量之间的依赖关系。如果P(Y)满足成对、局部或全局马尔科夫性，就此联合概率分布为概率无向图模型。

成对马尔科夫性

u和v是无向图G中任意两个没有边连接的结点，其他结点为O，成对马尔科尔性是指$Y_O$的条件下，$Y_u$和$Y_v$是条件独立的，即

$P(Y_u,Y_v|Y_O)=P(Y_u|Y_O)P(Y_v|Y_O)$

局部马尔科夫性

v是任意一个结点，W是与v存在边连接的所有节点，O是v和W以外的所有结点。局部马尔科夫性是指$Y_W$条件下，$Y_v$和$Y_O$是条件独立，即

$P(Y_v,Y_O|Y_W)=P(Y_v|Y_W)P(Y_O|Y_W)$

全局马尔科夫性

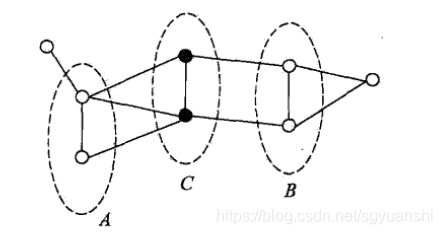
设结点集合A，B是被C分开的任意结点集合，全局马尔科夫性是指在$Y_C$的条件下，$Y_A$和$Y_B$是条件独立，即

$P(Y_A,Y_B|Y_C)=P(Y_A|Y_C)P(Y_B|Y_C)$

因子分解

团与最大团

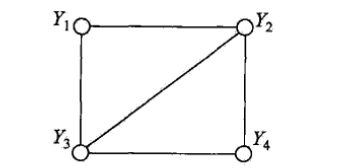
无向图G中任何两个结点均有边连接的结点集合称为团。若一个团，不能再加进任何一个结点使其成为更大的团，则称为最大团。

如$\{Y_2,Y_3\}$为团，$\{Y_1,Y_2,Y_3\}$为最大团。

概率无向图的联合概率分布P(Y)可以表示为：

$P(Y)=\frac{1}{Z}{\prod }_C{\Psi }_C(Y_C)$

$Z={\sum }_Y{\prod }_C{\Psi }_c(Y_C)$

其中，C为无向图的最大团，$Y_C$为C的结点对应的随机变量，${\Psi }_c(Y_C)$是C上定义的严格正函数。

二、条件随机场

**条件随机场：**设X与Y是随机变量，P(Y|X)是在给定X的条件下Y的条件概率分布。若Y构成一个由无向图G=(V,E)表示的马尔科夫随机场，即

$P(Y_v|X,Y_w,w\ne v)=P(Y_v|X,Y_w,w\sim v)$

$w\ne v$表示与结点v存在边连接的所有结点w，$w\sim v$表示结点v以外的所有结点

**线性链条件随机场：**设X和Y均为线性链表示的随机变量序列，P(Y|X)构成条件随机场，即满足马尔科夫性

$P(Y_i|X,Y_1,...,Y_{i-1},Y_{i+1},Y_n)=P(Y_i|X,Y_{i-1},Y_{i+1})$

$i=1,2,...,n$

在标注问题中，X表示输入观测序列，Y表示对应的输出标记序列或状态序列。

参数化形式

设P(Y|X)为线性链条件随机场，则：

$P(y|x)=\frac{1}{Z(x)}exp({\sum }_{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,x,i)+{\sum }_{i,l}{\mu }_l{s}_l(y_i,x,i))$

$Z(x)={\sum }_{y}exp({\sum }_{i,k}{\lambda }_k{t}_k(y_{i-1},y_i,x,i)+{\sum }_{i,l}{\mu }_l{s}_l(y_i,x,i))$

其中，$t_k$和$s_l$是特征函数，通常取值为1或0。${\lambda }_k$和${\mu }_l$是对应的权值，Z(x)是规范化因子。

$t_k$可以理解为定义在边上的特征函数：转移特征，与当前位置和前一个位置有关。

$s_l$是定义在结点上的特征函数：状态特征，只与当前位置有关。

简化形式

设有$K_1$个转移特征，$K_2$个状态特征，$K=K_1+K_2$，记

$f_k(y_{i-1},y_i,x,i)=\{\begin{array}{rl}& t_k(y_{i-1},y_i,x,i)\\ & s_l(y_i,x,i)\end{array}$

对各个位置i求和，记作

$f_k(y,x)={\sum }_{i=1}^n{f}_k(y_{i-1},y_i,x,i),k=1,2,...,K$

用$w_k$表示特征$f_k(y,x)$的权值，
$w_k=\{\begin{array}{l}{\lambda }_k,k=1,2,...,K_1\\ {\mu }_l,k=K_1+l;l=1,2,...,K_2\end{array}$

于是，上述的条件随机场可表示为：

$P(y|x)=\frac{1}{Z(x)}exp{\sum }_{k=1}^K{w}_k{f}_k(y,x)$

$Z(x)={\sum }_{y}exp{\sum }_{k=1}^K{w}_k{f}_k(y,x)$

若以w表示权值向量，即

$w=(w_1,w_2,...,w_k{)}^T$

以F(y,x)表示全局特征向量，即

$F(y,x)=(f_1(y,x),f_2(y,x),...,f_k(y,x){)}^T$

那么，条件随机场又可以写成w与F(y,x)內积的形式：

$P_w(y|x)=\frac{exp(w\ast F(y,x))}{Z_w(x)}$

三、RNN/LSTM下的条件随机场

根据上述条件随机场的定义，其实我们可以将条件随机场拆分为两部分，一部分就是转移特征函数：即$f(y_{i-1},y_i,x,i)$，每个时刻状态之间的转移关系，另一部分为$f(y_i,x,i)$，即每个时刻观测序列x与状态y之间的关系。

那么，条件随机场可以简化为：

$P(y|x)=\frac{1}{Z(x)}exp(h(y_1;x)+h(y_2;x)+g(y_1,y_2;x)+....+h(y_n;x)+g(y_{n-1},y_n;x))$

再接着，我们将观测序列x与状态y之间的关系交由RNN/LSTM去拟合，并且认为RNN/LSTM已经充分捕捉y与x之间的联系，因此，我们假定函数g与x无关，即

$P(y|x)=\frac{1}{Z(x)}exp(h(y_1;x)+h(y_2;x)+g(y_1,y_2)+....+h(y_n;x)+g(y_{n-1},y_n))$

到这里就比较简单了，

$h(y_t;x)$就是RNN网络在时刻t下状态为$y_t$的概率得分；

g其实就是转移矩阵了，$g(y_{n-1},y_n)$就是$y_{n-1}$转移到$y_n$概率。

模型训练

模型的参数包括RNN/LSTM的网络参数、转移概率矩阵参数。

求导、梯度下降等工作，我们可以交给tensorflow来处理，但首先，我们需要得到loss。

使用最大似然法进行训练，训练的目标就是最大化P(y|x)。因为它是包含自然数指数的，所以我们对其取对数，然后取相反数，变为最小化的最优化问题：

$-logP(y|x)=-\left(h(y_1;x)+{\sum }_{k=1}^{n-1}[g(y_k,y_{k+1})+h(y_{(}k+1);x)]\right)+logZ(x)$

归一化因子

最麻烦的还是这个归一化因子Z(x)，需要对所有路径进行指数求和。

假设我们状态y的取值有k种，那么就有k^n的量级，我们利用动态规划的思想进行递归，计算完时刻t的时候，将其存起来，直接用于时刻t+1。

首先，我们将$Z_t$分为k个部分：

$Z_t=Z_t^{(1)}+Z_t^{(2)}+....+Z_t^{(k)}$

$Z_t^{(1)},Z_t^{(2)},....,Z_t^{(k)}$是截止到时刻t，以状态(标签)1,…,k为终点的所有路径的得分指数和，

$Z_{t+1}^{(1)}=\left(Z_t^{(1)}{G}_{11}+Z_t^{(2)}{G}_{21}+....+Z_t^{(k)}{G}_{k1}\right)H_{t+1}(1;x)$

$Z_{t+1}^{(2)}=\left(Z_t^{(1)}{G}_{12}+Z_t^{(2)}{G}_{22}+....+Z_t^{(k)}{G}_{k2}\right)H_{t+1}(2;x)$

…

$Z_{t+1}^{(k)}=\left(Z_t^{(1)}{G}_{1k}+Z_t^{(2)}{G}_{2k}+....+Z_t^{(k)}{G}_{kk}\right)H_{t+1}(k;x)$

以矩阵的形式表示为：

$Z_{t+1}=Z_{t}G\ast H(y_{t+1};x)$

因为根据条件随机场的定理， 分布式指数分布的，所以在归一化因子中的计算也都是需要带上指数的。

G即为g的指数，H即为h的指数。

四、代码实现

import tensorflow as tf
import numpy as np
from tensorflow.contrib.crf import crf_log_likelihood


class BiLstmCrf:

    def crf_log_likelihood(self,
                           inputs,
                           tag_indices,
                           sequence_lengths,
                           transition_params=None):
        """Computes the log-likelihood of tag sequences in a CRF.

        Args:
          inputs: A [batch_size, max_seq_len, num_tags] tensor of unary potentials
              to use as input to the CRF layer.
          tag_indices: A [batch_size, max_seq_len] matrix of tag indices for which we
              compute the log-likelihood.
          sequence_lengths: A [batch_size] vector of true sequence lengths.
          transition_params: A [num_tags, num_tags] transition matrix, if available.
        Returns:
          log_likelihood: A [batch_size] `Tensor` containing the log-likelihood of
            each example, given the sequence of tag indices.
          transition_params: A [num_tags, num_tags] transition matrix. This is either
              provided by the caller or created in this function.
        """
        max_seq_len = inputs.get_shape().as_list()[1]
        num_tags = inputs.get_shape().as_list()[2]

        # LSTM的发射矩阵的累计得分
        mask = tf.sequence_mask(sequence_lengths, max_seq_len, dtype=tf.float32)
        inputs = inputs * tf.expand_dims(mask, axis=-1)
        sequence_score = inputs * tf.one_hot(tag_indices, depth=num_tags, dtype=tf.float32)
        sequence_score = tf.reduce_sum(tf.reduce_sum(sequence_score, axis=-1), axis=-1)

        # 转移概率累计得分
        transition_score = tf.gather(transition_params, axis=0, indices=tag_indices[:, :-1]) * tf.expand_dims(
            mask[:, 1:], axis=-1) * tf.one_hot(tag_indices[:, 1:], depth=num_tags, dtype=tf.float32)
        transition_score = tf.reduce_sum(tf.reduce_sum(transition_score, axis=-1), axis=-1)

        # 归一化因子计算
        alpha = [inputs[:, 0, n:(n + 1)] for n in range(num_tags)]  # [batch_size, num_tags]
        for t in range(1, max_seq_len):
            temp = alpha.copy()
            for n in range(num_tags):
                alpha[n] = tf.where(tf.equal(mask[:, t:(t + 1)], 1), tf.reduce_logsumexp(
                    tf.concat(temp, axis=-1) + tf.transpose(transition_params[:, n:(n + 1)]), axis=-1,
                    keepdims=True) + inputs[:, t, n:(n + 1)], temp[n])

        log_norm = tf.reduce_logsumexp(tf.concat(alpha, axis=-1), axis=-1)

        return log_norm - (sequence_score + transition_score)


if __name__ == '__main__':
    inputs_arr = np.random.random([20, 10, 5])
    tag_indices_arr = np.random.randint(0, 5, [20, 10])
    transition_params_arr = np.random.random([5, 5])
    sequence_lengths_arr = np.random.randint(0, 10, [20])

    inputs = tf.placeholder(tf.float32, [None, 10, 5])
    tag_indices = tf.placeholder(tf.int64, [None, 10])
    transition_params = tf.placeholder(tf.float32, [5, 5])
    # sequence_lengths = np.full([100], 10)
    sequence_lengths = tf.placeholder(tf.int64, [None])

    sess = tf.Session()

    crf = BiLstmCrf()
    res1 = crf.crf_log_likelihood(inputs,
                                  tag_indices,
                                  sequence_lengths,
                                  transition_params)
    # tensorflow自带的crf函数
    res2 = crf_log_likelihood(inputs,
                              tag_indices,
                              sequence_lengths,
                              transition_params)
    feed_dict = {inputs: inputs_arr, tag_indices: tag_indices_arr, sequence_lengths: sequence_lengths_arr,
                 transition_params: transition_params_arr}
    print(sess.run(res1, feed_dict=feed_dict))
    print(sess.run(res2, feed_dict=feed_dict))

tensorflow迭代计算

在归一化因子的迭代计算时，其实可以用tensorflow中的rnn相关的api来代替

因子RNN其实一直在迭代计算$h_{t+1}=f(h_t,x)$
（里面的array_os、math_os是tensorflow下的api，与正常的tf用法基本一致）

# Split up the first and rest of the inputs in preparation for the forward
# algorithm.
first_input = array_ops.slice(inputs, [0, 0, 0], [-1, 1, -1])
first_input = array_ops.squeeze(first_input, [1])

"""Forward computation of alpha values."""
rest_of_input = array_ops.slice(inputs, [0, 1, 0], [-1, -1, -1])

# Compute the alpha values in the forward algorithm in order to get the
# partition function.
forward_cell = CrfForwardRnnCell(transition_params)
# Sequence length is not allowed to be less than zero.
sequence_lengths_less_one = math_ops.maximum(
    constant_op.constant(0, dtype=sequence_lengths.dtype),
    sequence_lengths - 1)
_, alphas = rnn.dynamic_rnn(
    cell=forward_cell,
    inputs=rest_of_input,
    sequence_length=sequence_lengths_less_one,
    initial_state=first_input,
    dtype=dtypes.float32)
log_norm = math_ops.reduce_logsumexp(alphas, [1])
# Mask `log_norm` of the sequences with length <= zero.
log_norm = array_ops.where(math_ops.less_equal(sequence_lengths, 0),
                           array_ops.zeros_like(log_norm),
                           log_norm)

class CrfForwardRnnCell(rnn_cell.RNNCell):
    """Computes the alpha values in a linear-chain CRF.

    See http://www.cs.columbia.edu/~mcollins/fb.pdf for reference.
    """

    def __init__(self, transition_params):
        """Initialize the CrfForwardRnnCell.

        Args:
          transition_params: A [num_tags, num_tags] matrix of binary potentials.
              This matrix is expanded into a [1, num_tags, num_tags] in preparation
              for the broadcast summation occurring within the cell.
        """
        self._transition_params = array_ops.expand_dims(transition_params, 0)
        self._num_tags = transition_params.get_shape()[0].value

    @property
    def state_size(self):
        return self._num_tags

    @property
    def output_size(self):
        return self._num_tags

    def __call__(self, inputs, state, scope=None):
        """Build the CrfForwardRnnCell.

        Args:
          inputs: A [batch_size, num_tags] matrix of unary potentials.
          state: A [batch_size, num_tags] matrix containing the previous alpha
              values.
          scope: Unused variable scope of this cell.

        Returns:
          new_alphas, new_alphas: A pair of [batch_size, num_tags] matrices
              values containing the new alpha values.
        """
        state = array_ops.expand_dims(state, 2)

        # This addition op broadcasts self._transitions_params along the zeroth
        # dimension and state along the second dimension. This performs the
        # multiplication of previous alpha values and the current binary potentials
        # in log space.
        transition_scores = state + self._transition_params
        new_alphas = inputs + math_ops.reduce_logsumexp(transition_scores, [1])

        # Both the state and the output of this RNN cell contain the alphas values.
        # The output value is currently unused and simply satisfies the RNN API.
        # This could be useful in the future if we need to compute marginal
        # probabilities, which would require the accumulated alpha values at every
        # time step.
        return new_alphas, new_alphas

五、模型预测

维特比(Viterbi)算法