正则化线性回归的偏差和方差（Octave转换为Python）

详细代码参考github

利用正则化线性回归模型来了解偏差和方差的特征

实例：
首先根据数据建立线性回归模型，模型能够根据水库液位的变化来预测大坝的排水量，然后通过调整参数等方法来学习偏差和方差的一些特性。

1.概念

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力；
方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响（模型的稳定性）。

2.构建正则化线性模型

（1）载入数据

打开数据集ex5data1.mat，数据集包含了以下内容：

名称	维度
X	(12, 1)
y	(12, 1)
Xtest	(21, 1)
ytest	(21, 1)
Xval	(21, 1)
yval	(21, 1)

其中：
X，y是训练集，用来训练模型；
Xval，yval是交叉验证集，主要用来确定模型中的超参数，如正则化参数lambda；
Xtest，ytest是测试集，主要评估模型的泛化能力。

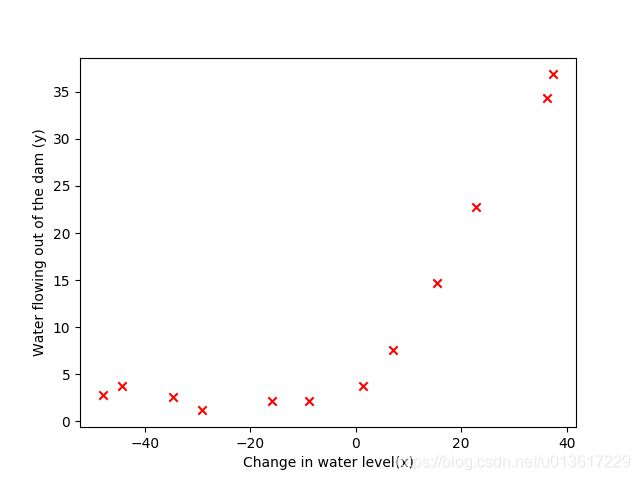
（2）将X，y可视化

横轴表示水位的变化，纵轴表示水流量，单纯的线性回归也能计算出模型，但那样做偏差特别大，拟合程度很差，即出现欠拟合。

参考代码：

def plotXY(self, x, y):
	plt.scatter(x, y, marker='x', color='r')
	plt.xlabel('Change in water level(x)')
	plt.ylabel('Water flowing out of the dam (y)')
	plt.show()

（3）计算正则化线性回归损失函数J

损失函数公式如下，注意正则化项是从下标1开始计算的，lambda就是正则化系数，它控制模型复杂度的"惩罚"力度。

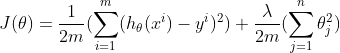
（4）计算正则化线性回归梯度Gradient

损失函数J对theta0和theta1的偏导数定义如下，即要计算的梯度公式。


参考代码：

   def linearRegCostFunction(self, theta, x, y, lamda):
   m = x.shape[0]
   theta = theta.reshape((x.shape[1], 1))
   cost = np.sum((x.dot(theta)-y)**2)/(2*m)
   regular = lamda/(2*m)*np.sum(theta[1::]**2)
   J = cost + regular
   return J

def linearRegGradient(self, theta, x, y, lamda):
   m = y.shape[0]
   theta = theta.reshape((x.shape[1], 1))
   grad = np.zeros((x.shape[1], 1))
   grad[0] = 1/m*(x[:, 0:1].T.dot(x.dot(theta)-y))
   grad[1::] = 1/m*(x[:, 1::].T.dot(x.dot(theta)-y)) + lamda/m*theta[1::]
   return grad

（5）拟合线性回归

当我们根据上述公式计算损失函数和梯度得到正确的结果后，我们利用之前提到的scipy.optimize中的minimize函数来计算最优的theta0和theta1，计算得到theta的结果后，将lambda的值设为0，因为当前模型只有theta1和theta2两个值，模型很简单，没必要设置正则化项。

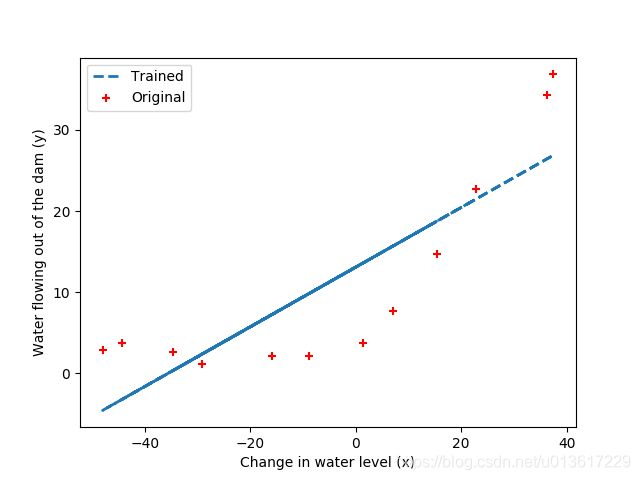
将得到的theta值同X相乘，得到预测的y_predict，将结果进行绘制，得到拟合的结果，如下图。

可以看出得到的结果并不好，在接下来的内容里，我们逐步讨论。

参考代码：

def plotTrainingLine(self, x, y):
	theta = self.trainLinearReg(x, y, 0)
	plt.scatter(self.x, self.y, marker='+', color='r')
	plt.plot(self.x, x.dot(theta), '--', linewidth=2)
	plt.xlabel('Change in water level (x)')
	plt.ylabel('Water flowing out of the dam (y)')
	plt.legend(['Trained', 'Original'])
	plt.show()

3.方差和偏差

（1）绘制学习曲线

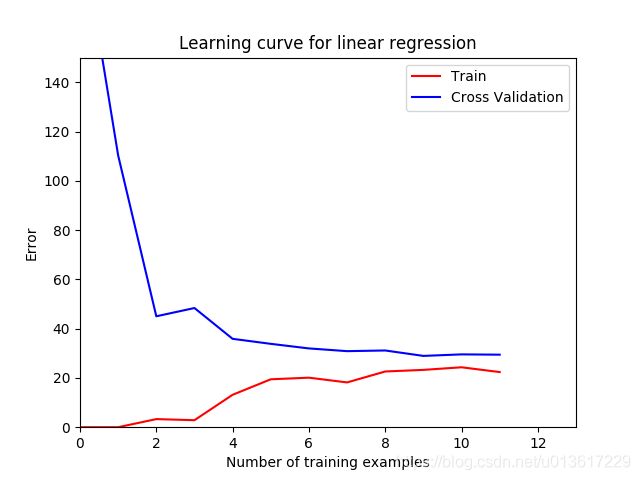
绘制训练集和交叉验证集的误差与训练样本数量之间的学习曲线，注意： 训练集误差和交叉验证集误差都没有计算正则化项，后面我们单独讨论正则化系数对误差造成的影响。

观察下图，随着样本数量逐渐增加，训练集和交叉验证集之间的误差仍然是较大的，这就反应了模型的高偏差问题，即欠拟合。

因为模型太简单了，不能很好的拟合我们的数据，接下来我们将训练模型修改，建立一个8次多项式。

参考代码：

def learningCurve(self, x, y, xval, yval, lamda):
	m = x.shape[0]
	error_train = np.zeros((m, 1))
	error_val = np.zeros((m, 1))
	print("Training Examples\tTrain Error\tCross Validation Error\n")
	for i in range(m):
		theta = self.trainLinearReg(x[:1+i, :], y[:1+i], lamda)
		error_train[i] = self.linearRegCostFunction(theta, x[:1+i, :], y[:1+i], 0)
		error_val[i] = self.linearRegCostFunction(theta, xval, yval, 0)
		print("\t\t%d\t\t\t%f\t\t%f\n"%(i, error_train[i], error_val[i]))
	return [error_train, error_val]

def plotLinerRCurve(self):
	error_train, error_val = self.learningCurve(self.x_plus_one, self.y, self.xval_plus_one, self.yval, 0)
	plt.xlim([0, 13])
	plt.ylim([0, 150])
	plt.plot([i for i in range(12)], error_train, 'r')
	plt.plot([i for i in range(12)], error_val, 'b')
	plt.title('Learning curve for linear regression')
	plt.xlabel('Number of training examples')
	plt.ylabel('Error')
	plt.legend(['Train', 'Cross Validation'])
	plt.show()

（2）建立多项式回归模型

由于一次线性模型太简单，导致欠拟合，我们添加更多的"特征"，做一个八次多项式。具体最高项应该设置成几次这个问题，也是没有定式，只能说多尝试，找到较为合适的最高次数。
参考代码：

def polyFeatures(self, x, p):
	x_ploy = np.zeros((np.size(x), p), np.float32)  # (12, 8)
	m = np.size(x)  # 12
	for i in range(m):
		for j in range(p):
			x_ploy[i, j] = x[i]**(j+1)
	return x_ploy

（3）绘制多项式回归模型拟合曲线

根据上一部分得到的多项式，因为同样是解决一个线性回归的问题，所以之前的损失函数和梯度计算函数仍可使用。

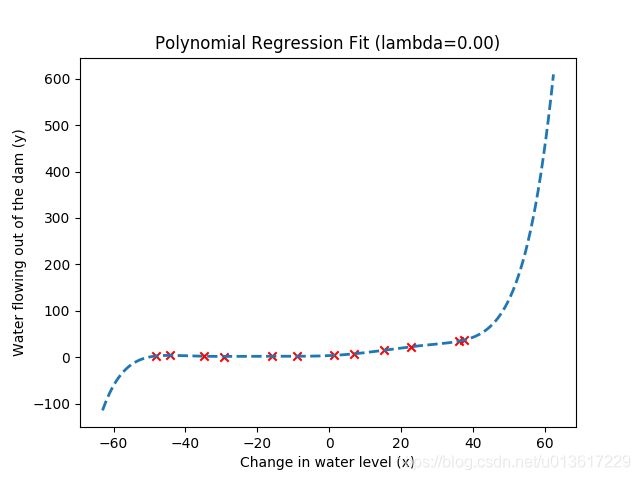
接下来利用优化函数计算得到最优的theta值，绘制拟合曲线，当设置正则化系数lambda=0的时候，意味这对模型复杂度没有任何处理，得到下图。

可以看出，我们的模型训练的非常好，基本穿过了每一个点，训练误差肯定很小，但是在一些极值外，函数迅速的上升和下降，这就意味这我们设计的模型过拟合了，虽然对训练数据拟合很好，但是不具有很好的泛化能力，也意味着模型不稳定。

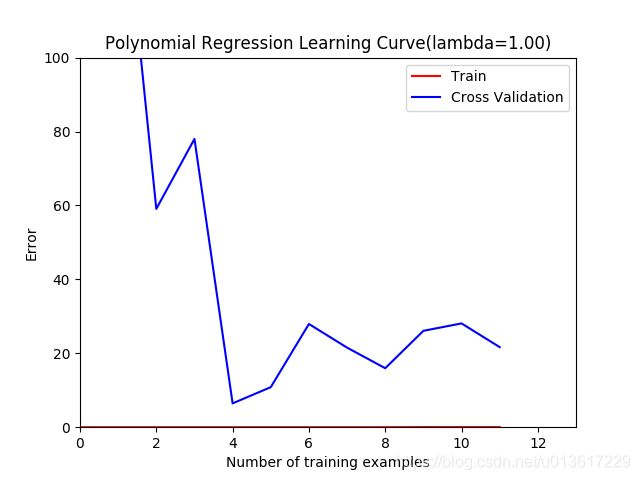
观察下lambda=0的情况下，训练误差和交叉验证误差的曲线，非常明显，训练误差几乎为0，而交叉验证误差却很大，训练集和交叉验证集之间的空隙充分反应了模型的高方差问题。

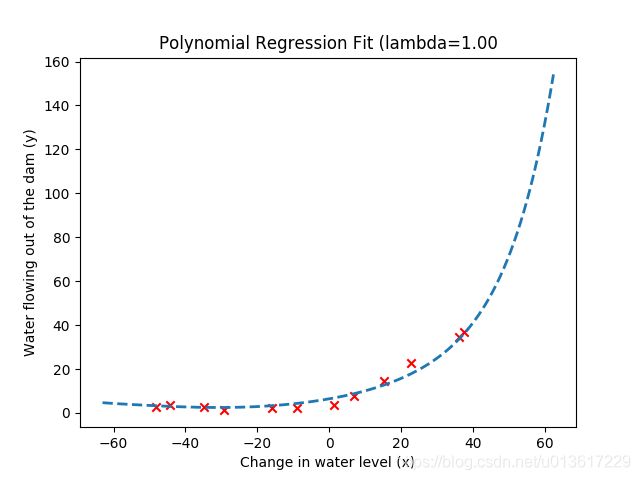
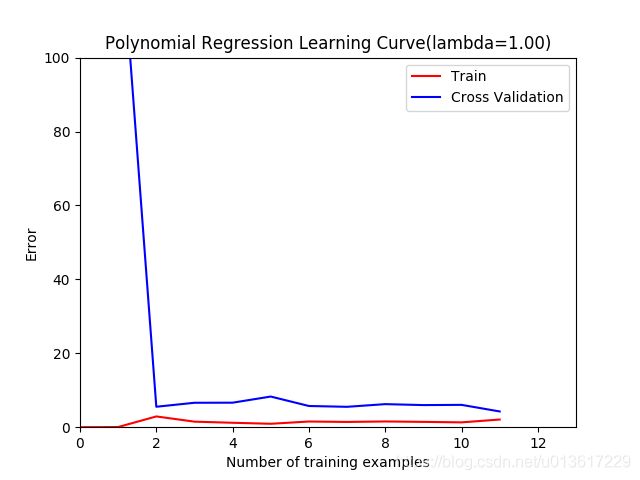
此时我们让正则化系数为1，再重复上面的试验，我们再来看下你和曲线和学习曲线的图形。

一目了然，多项式模型很好的拟合了数据，训练误差和交叉验证集误差曲线都随着样本数量的增加都收敛于一个较小的值，因此我们认为当lambda=1时，得到的模型没有高偏差和高方差的问题，实际上也是模型在方差和偏差之间进行了很好的折中。


参考代码：

def plotFit(self, x, mu, sigma, theta, p):
	x = np.arange(np.min(x) - 15, np.max(x) + 25, 0.05)
	x = x.reshape((-1, 1))
	x_poly = self.polyFeatures(x, p)
	x_poly = x_poly - mu
	x_poly = x_poly/sigma

	x_poly = np.hstack([np.ones((x_poly.shape[0], 1)), x_poly])
	plt.plot(x, x_poly.dot(theta), '--', linewidth=2)
	plt.title('Polynomial Regression Fit (lambda=0.00)')
	plt.xlabel('Change in water level (x)')
	plt.ylabel('Water flowing out of the dam (y)')
	plt.show()

（4）利用交叉验证集选择lambda

通过上面的试验，我们可以知道，lambda明显的影响着多项式正则化回归的训练误差和交叉验证误差。当lambda为0甚至很小的时候，模型可以很好的拟合训练集，不具备好的泛化能力，当lambda很大的时候，模型又不能很好的拟合数据，出现欠拟合问题，那么到底怎样选择一个lambda的值呢？

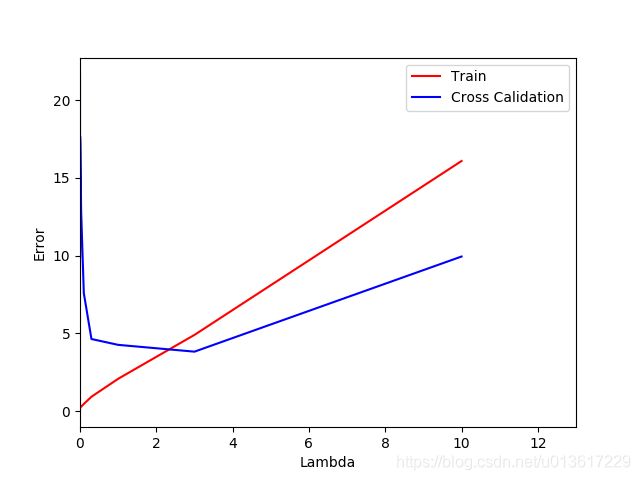
我们根据上面的实例，选择10个lambda的值，分别绘制每个lambda对应的训练误差和交叉验证集误差，
lambda_vec = {0; 0:001; 0:003; 0:01; 0:03; 0:1; 0:3; 1; 3; 10}

绘制得到下图， 从图中我们可以看出最好的lambda值出现在3附近，此时测试误差值大约3.8599，结果已经相当不错了。

参考代码：

def validationCurveForLamdas(self, x, y, xval, yval, lamda_vec):
	error_train = np.zeros((len(lamda_vec), 1))
	error_val = np.zeros((len(lamda_vec), 1))
	print("Lambda\t\tTrain Error\tValidation Error\n")
	for i in range(len(lamda_vec)):
		lamda = lamda_vec[i]
		theta = self.trainLinearReg(x, y, lamda)
		error_train[i] = self.linearRegCostFunction(theta, x, y, 0)
		error_val[i] = self.linearRegCostFunction(theta, xval, yval, 0)
		print("\t\t%d\t\t\t%f\t\t%f\n" % (i, error_train[i], error_val[i]))
	return [error_train, error_val]