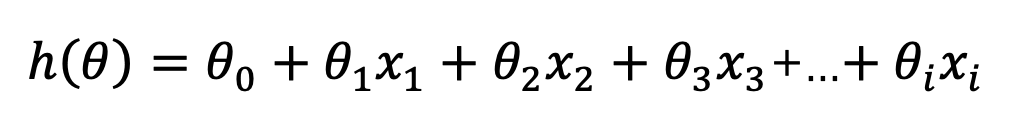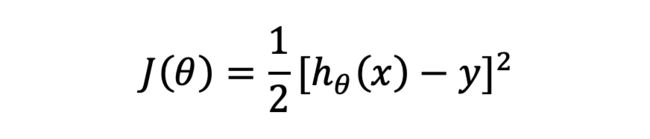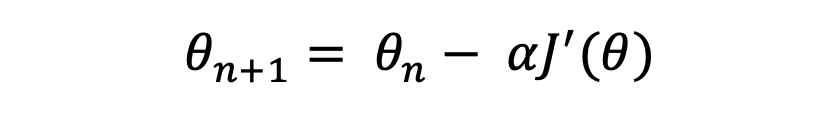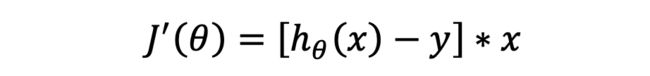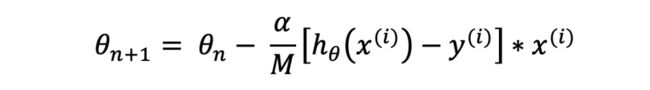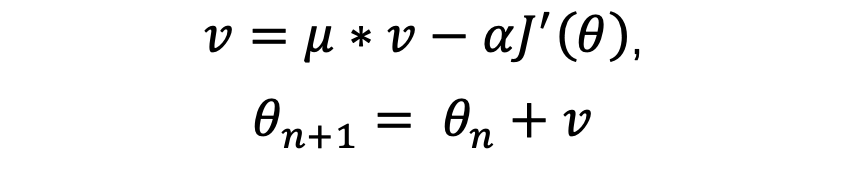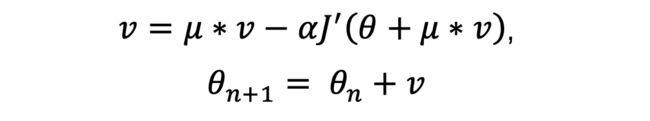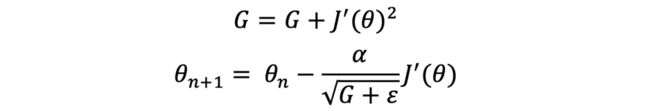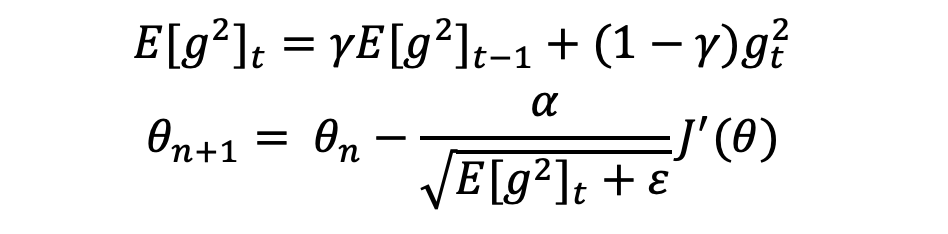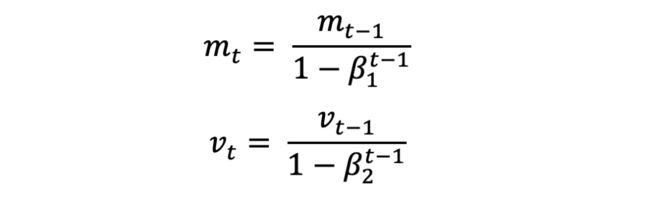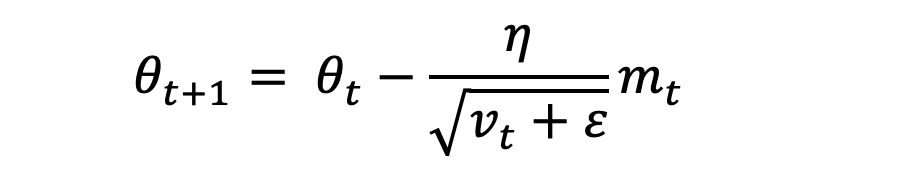梯度下降法详解

前言

梯度下降法

梯度下降法是机器学习中一种常用到的算法，主要解决求最小值问题，其基本思想在于不断地逼近最优点，每一步的优化方向就是梯度的方向。

对于最简单的线性回归问题，

我们假设其损失函数

那么梯度下降的基本形式就是

其中，为学习率(learning_rate)。下一步便是要将损失函数最小化，需要对J(θ)求导：

 

我们来看看是什么样子的。

所以

可得

常用的梯度下降法包括随机梯度下降法(SGD)、批梯度下降法(BGD)、Momentum梯度下降法、Nesterov Momentum梯度下降法、AdaGrad、RMSprop、AdaDelta、Adam。下面我们分别对其进行介绍。

 

 

随机梯度下降法(SGD)

所谓随机梯度下降法，指的是每次随机从样本集中抽取一个样本对进行更新：

这种算法如果要遍历整个样本集的话需要迭代很多次，且每次更新并不是向着最优的方向进行，所以每走一步都要很小心。

而标准梯度下降法则是计算样本集中损失函数的总和之后再对参数进行更新：

这种算法是在遍历了整个样本集之后才对参数进行更新，因此它的下降方向是最标准的方向，所以它就可以很理直气壮的走每一步。因此，这种算法的学习率一般要比随机梯度下降法的大。

当损失函数的局部极小值较多时，随机梯度下降法(SGD)能够较好地避免局部极小值。

批梯度下降法

这种算法解决了传统的梯度下降法的缺点，它每次随机从样本集中抽取batch_size个样本进行迭代：

这种算法精度较高，同时收敛速度也很快。

Momentum梯度下降法

损失函数的梯度，可以看过施加给小球的力，通过力有了速度，通过速度改变位置。由力学定律。梯度与加速度成正比，加速度改变速度，因此可以得到以下更新过程：

其中，μ是动量系数，即一个方向的速度并不是立刻改变，而是速度通过积累一点点改变，μμ值得大小，可以通过trian-and-error来确定，实践中常常设为0.9。

这种算法的原理在于一个方向的速度可以积累，而且越积累越大；通过不同训练样本求得梯度时，在最优的方向的梯度，始终都会增大最优方向上的速度。因此，可以减少许多震荡。

Nesterov Momentum梯度下降法

Nesterov Momentum梯度下降法是对Momentum梯度下降法的一个改进。在Momentum梯度下降法中，已经求出了μ∗vμ∗v，那么可以再“向前看一步”，不是求解当前位置的梯度，而是求解θ+μ∗vθ+μ∗v处的梯度。这个位置虽然不正确，但是要优于当前位置θ。

AdaGrad

学习率在梯度下降法中，十分重要，但是所有参数都是用同一个学习率未必合适。例如，有些参数可能已经接近最优，仅仅需要微调，需要比较小的学习率；而有些参数还需要大幅度调动。在这种场景下，AdaGrad，来自适应不同的学习率。

AdaGrad原理也比较简单，它通过记录之前更新每一步更新值的平方，将这些参数累加，以此来调节每一步的学习率。

如果梯度比较大，它会不断减小学习率；相反，则会增大。

缺点是，随着训练进行，学习率会不断减小，最终参数不再更新。

RMSprop

AdaDelta也是为了解决Adagrad中，学习率不断减小问题的。与Adagrad不同的是，AdaDelta通过设置窗口w，只是用部分时间段内累计的梯度。存储前w个梯度：

Adam

Adam考虑了梯度以及梯度的平方，具有AdaGrad和AdaDelta的优点。Adam根据梯度的一阶估计和二阶估计，动态调整学习率。

其中，m(t)为梯度的第一时刻平均值，v(t)为梯度的第二时刻非中心方差值，其中，β1设为0.9，β2设为0.9999，ϵ设为10e-8。

这种优化算法不仅存储了AdaDelta先前平方梯度的指数衰减平均值，而且保持了先前梯度M(t)的指数衰减平均值，这一点与动量类似。

梯度下降法和其他无约束优化算法的比较

　　　　在机器学习中的无约束优化算法，除了梯度下降以外，还有前面提到的最小二乘法，此外还有牛顿法和拟牛顿法。

　　　　梯度下降法和最小二乘法相比，梯度下降法需要选择步长，而最小二乘法不需要。梯度下降法是迭代求解，最小二乘法是计算解析解。如果样本量不算很大，且存在解析解，最小二乘法比起梯度下降法要有优势，计算速度很快。但是如果样本量很大，用最小二乘法由于需要求一个超级大的逆矩阵，这时就很难或者很慢才能求解解析解了，使用迭代的梯度下降法比较有优势。

　　　　梯度下降法和牛顿法/拟牛顿法相比，两者都是迭代求解，不过梯度下降法是梯度求解，而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言，使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。